Tuesday, 11 April 2006
The Phil Ehrlich Experience

When you attend a lunchtime talk at the Center, you expect a lunchtime talk. But when Phil Ehrlich is on the menu, you'll have quite another experience. The topic seems simple enough. There are ordinary real numbers, 2, -1.5, pi, e and so on. And there are continuous magnitudes, like distances in space or masses or temperatures. We usually assume that knowing all about the reals means we know all about theses sorts of continuous magnitudes.

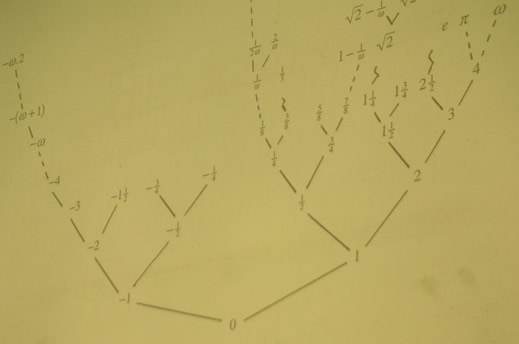
That would be our first mistake, we soon learn. For over a century mathematicians have known of theories of continuous magnitudes that have much more in them than real numbers. They have infinitesimal magnitudes, smaller than any positive real number, but bigger than zero; and a plethora of infinitely great magnitudes, bigger than any real.

And our second mistake would be to think that this is minor technical issue. It is, Phil asserts with rising passion, the central problem in the foundations of mathematics. At this point, we are glimpsing the fascinations that drive Phil's gentle smile.

There are many theories of these numbers great and small. What Phil wants to show us today is what promises to be the grand theory that embraces them all. It is Conway's big number system "No." Its construction starts with a tree with 0 at the root. That branches to -1 and 1; and the 1 to 1/2 and 2; and the 2 to 1 1/2 and 3; and so on. And so on. And so on; until this swelling, branching tree has all the rational numbers and all the real numbers and all the infinitesimals and all the infinities. "It blossoms, and blossoms, and blossoms!"

Phil's face glows like a father cradling his newborn, seeing all the potential that is to come. He explains with energetic sweeps and waves how he is proving that this one structure contains within it all the theories of numbers, big and small. While there may be infinitely many of these numbers, Phil seems to have a personal attachment to every one of them. "They all have proper names!" he beams. He starts to write up some names on the blackboard. "Pi over omega minus root omega over omega squared." They behave just like the numbers you learned about at school. You multiply two omega squared by four omega to the fourth just as you'd expect. You get eight omega to the sixth. "All kinds of delightful numbers like these!" he says.

It is only later that I learn from him that most of these names are infinitely big. They have to be. There are too many numbers to name finitely. So if a name is a something squared, we'll unpack the something into more parts: a something or other and a something else; and then we'll unpack these parts into more; and so on, indefinitely, like a magician endlessly pulling rabbits and doves out of his fist.

Then we turn to non-standard analysis. "This is simply standard, non-standard analysis," he assures us, not realizing quite what he said. "We'll just get a flavor," Phil assures us, "there's no way I can go through all of this!"

We have no doubt of that, as Phil jumps back and forth between the blackboard and the overhead projector screen, covered with dense quotes from heroes and antiheroes, and his limitless joy sweeps us along. "Here's a rather recent result. This one is really, really interesting." "It really surprized me. It's really delightful." This is more than a talk. It is like gazing into a volcano. The dark crust of rock breaks here and there and the lava spills through, white hot, glowing and unstoppable.

Question time is eager. Well after it is over I glance into the seminar room. Phil is still at the blackboard, hemmed in by interrogators, beaming.

John D. Norton

Philip Ehrlich, Ohio University
Tuesday, 11 April 2006
::: The Absolute Arithmetic
    Continuum and the Unification of
    All Numbers Great and Small
::: Lunchtime Colloquium