Galileo Exonerated
Lunchtime Talk
28 February 2012

In 1638, an ailing, aged Galileo, under house arrest, published his Discourses on Two Sciences. This great work laid the foundations of the modern sciences of statics and dynamics. Its most celebrated result is its law for falling bodies: the distances they fall increase with the square of the times; or, equivalently, their speeds grow in proportion to time. This last result was hard won. Decades earlier, Galileo had taken up with an alternative law. It said that the speeds of falling bodies grow in proportion to the distances fallen, not the times.

Galileo had to pass beyond this hurdle before he could complete his great work. We have few clues on how Galileo passed it. The strongest is a short argument in the Third Day of the discourses. Sagredo raises the question of the speed-distance law. Salviati, the wisest of the three discussants, responds by offering a "very clear proof" of the falsity and impossibility of the law.

What follows this promise by Salviati is a short paragraph of argumentation. It concludes that motion under the speed-distance law must be instantaneous, that is, infinitely fast. For over 350 years, Galileo commentators have struggled to make sense of this "very clear proof." To them it has been anything but clear and, at its worst, just looks like an exercise in circular reasoning.

Decades ago, while a graduate student, I had read this part of the Discourses  and found the argument baffling. It was irksome that an otherwise lucid Galileo should suddenly collapse into confusion or sophistry on a point that must have been pivotal in redirecting his own thinking. But then even our heroes like Galileo are not beyond impenetrable confusions. Or so I reluctantly supposed.

Bryan Roberts is finishing his doctorate in the Department of History and Philosophy Science. He is one of the brightest of a new generation of philosophers of physics and now thinks mostly about time in quantum theory. The delightful thing about smart people is that they make the people around them smarter. He worked this magic on me.

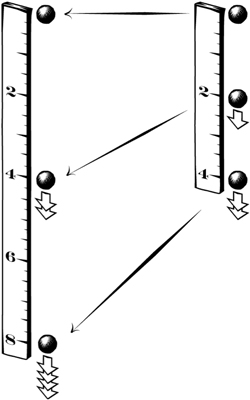
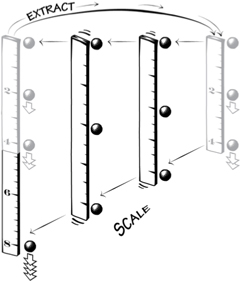
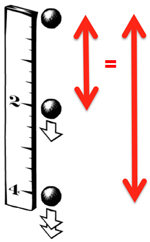
A few years ago, he had been engaged in an historical project. It was an analysis of a paper by Pierre Fermat that had picked up on Galileo's work on a speed-distance law of fall. We had talked about it. The magic did its work. Between us we suddenly found that we could make sense of the baffling paragraph in Discourses. It was a wonderful moment. Somehow, I felt, a little misplaced piece of the world had been set right.

This clarification was the subject of my talk today. Jim Woodward made the introduction, with Bryan sitting prominently in the front to rescue me from hard questions. Once you see it, I assured the group that had assembled for the talk, it is simple and powerful. Galileo has a terrific argument. It works both by his own standards and by modern standards, but with just one blemish in the final step.

The key to the reading is the first clause:

"When speeds have the same ratio as the spaces passed or to be passed, those spaces come to be passed in equal times;. . . "

Salviati had led into this clause by talking about motion under the speed-distance law of fall. It is natural to assume that this clause applies to just ONE motion of fall. That natural assumption leads to disaster. For then the remainder of the argument collapses into a circularity. What Bryan and I now realized was that one could read the "speeds" (plural) and "spaces" (plural) as referring to TWO motions. Then this first clause describes what happens when one takes one motion, any motion, and scales its speeds and distances by the same factor to create a second motion: the two motions take place in the same time.

Why would one adopt this alternate reading? The reason is simple. Under it, things work out. The next step of Galileo's argument notes that motion under the speed-distance law specifically has the property of self-similarity. If one scales up the first part of the motion, one recovers the whole motion.

Putting the two pieces together gives the final result. Motion under the speed-distance law of fall has the odd property that it takes the same time to pass half the distance as all the distance.

Everything that Galileo has argued up to this "equal time" result is correct, both by Galileo's 17th century standards and by our modern standards. Then it falls apart in the final step. Galileo announces that the time of fall that satisfies this "equal time" result is zero time. That means that the body falls infinitely fast, which immediately contradicts our experience of falling bodies (and also looks rather strange).

What has gone wrong? One could be excused from imagining that fall under the speed-distance law is not so different from fall under the celebrated speed-time law. However that is not so. Fall under the speed-distance law is peculiar. It is an exponential growth of distance with time, under both a 17th century and a modern analysis. As we trace the position of the falling body backwards in time, it gets closer and closer to its starting point of rest. But it never actually gets there. That is, if the body is falling now, it must have been falling for all time in the past. More tersely, it needs infinite time to fall to its present position.

It is not so easy to see how this can be, even if one has more modern mathematical sophistication. However the remarkable thing is that Galileo was on the threshold of recovering these properties of motion in the final step of his analysis. The "equal time" result is satisfied by a zero time of fall. It is also satisfied by an infinite time of fall. If the falling body takes an infinity of time to reach its present position under the speed-distance law, it had already been falling for an infinity of time to arrive at the halfway point.

Galileo did miss the mark in the end. But it was a near miss that successfully replicated many of the properties of an odd motion. It failed only by overlooking some delicate points to do with the ever troublesome infinity. Understood this way, it was an analysis worthy of a Galileo.

If you are ready now to condemn Galileo for missing this infinite time option, you should note that the infinity itself is only the start of the oddities. Here's another. The motion takes an infinity of time to cover a finite distance. If we compute the average speed we have:

distance/time = finite/infinite = zero

The motion has average speed zero, but at every moment of time for all eternity of the past, the instantaneous speed is greater than zero. The body is always falling in the same direction, but its average speed is zero. One might well think that logically impossible. But here we have it.

I did my best to explain all this simply and clearly. I had some lovely figures, mostly drawn by Bryan's artistic hand. Once you "get it," as Bryan and I had a few years ago, it all seems so simple. But we knew that our enthusiasm for the analysis did not readily infect all readers. We knew this specifically to be the case with referees at four journals. After dealing with them, we felt that we had heard every objection that could reasonably be hurled at us and many more that were unreasonable.

When questions were opened, we were pleased to find that at least some of our audience was convinced. There were also familiar complaints. A lively exchange over them took up most of question time. Were we being unkind to the existing literature? (No. While it has many insights, it has failed on this particular argument.) Was the scaling result really a result that Galileo had proved? (No. But our analysis requires only that Galileo assert it as the first step, not derive it.) Isn't the infinite time case really just the case of "v=0"; that is, no motion at all? (No. The infinite time case is one in which the instantaneous speed is never zero. Only the average speed is zero.)

We had expected a reception something like this, but it was still disheartening. I suppose we should expect resistance. We have come to the seminar room, stood brashly with our fancy digital slides and claimed smugly to have solved a mystery that has defeated commentators for more than 350 years. And the solution, we announce glibly, is so simple we can show it in a few pictures. That takes hubris! A diligent audience cannot let that slip by. There's got to be some trick, some flaw, some subterfuge, and it had better be put on record that this audience, this day was not taken in. Or at least I think that is a part of the reason for the resistance.

I suppose it might just be too good to be true and we have erred in some way we do not know. However here, quietly, just between us, I will confess to a little vanity and a little shameful smugness. We do think we have it right.

If you want to see the details, there is a preprint of the paper on philsci-archive

Norton, John D. and Roberts, Bryan W. (2010)
"Galileo's Refutation of the Speed-Distance Law of Fall Rehabilitated"

at http://philsci-archive.pitt.edu/5479.

Centaurus is publishing the final version, along with comments from critics and our response them.

John D. Norton