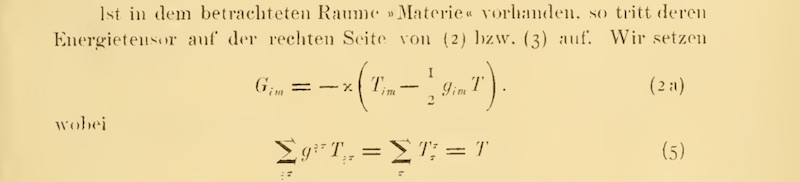| HPS 0410 |
Einstein for Everyone |
|
Back
to main course page
Einstein's Pathway to General Relativity
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Linked document: Uniform
Acceleration in a Minkowski Spacetime
We have followed a simple pathway to the main ideas of the
general theory of relativity. We started with the geometrical notion of
the curvature of space and saw how that
geometrical notion can be extended from space to spacetime. We then found
the resulting theory of curved spacetime not just to cover a curved
geometry of space, but gravitational phenomena as well.
This pathway to the theory was not Einstein's. His was
more indirect, more inspired, more tortured and more fallible. The final
theory emerged after Einstein struggled for seven
years with many things: strong hunches about what the theory
should say physically, vivid thought experiments to support the hunches,
lengthy explorations into new mathematics, errors and confusions that
thoroughly derailed him and a final insight that rescued him from
exhaustion and desperation.
1907
1908
1910
1911
1912
1912-1913
1913
1914
1915
|
The seven years of work divides loosely into two
phases.
The earlier phase of his work from 1907
to 1912 was governed by powerful physical intuitions that seemed as
much rationally as instinctively based. Einstein felt a compelling
need to generalize the principle of relativity from inertial motion
to accelerated motion. He was transfixed by the ability of
acceleration to mimic gravity and by the idea that inertia is a
gravitational effect. These ideas finally issued in a theory of
static gravitational fields in 1912. In it, gravity bends light and
slows clocks and the speed of light varies from place to place.
The major transition to general
relativity came after the summer of 1912 and into early 1913.
Einstein struggled to incorporate these ideas into a more general
physical theory. He was drawn to use the mathematics of curvature as
a means of formulating the new theory. To learn the mathematics, he
collaborated with his mathematician friend, Marcel Grossmann.
Together, they produced the first draft of the general theory of
relativity.
The remaining years, 1913 to 1915, were devoted to the labored work
of correcting and perfecting his draft of 1913. As the mathematics
of curvature took a more controlling position in the later phases,
Einstein's work began to change. The
theorizing was governed increasingly by notions of mathematical
simplicity and naturalness. When the theory was completed,
Einstein's starting point was quite distant. |

|
It is impractical in this chapter to review all
these considerations. Einstein's intricate mathematical struggles in
the later years cannot easily be described in informal terms.
However some of his earlier physical reflections are so famous and
so characteristic of Einstein, that
they must be mentioned.
Finally a caution to those seeking to learn general relativity from
these pages. The considerations below are the ones that guided
Einstein towards general relativity. Whether these guides persist as
founding principles of general relativity remains debated today. In
particular, there is increasing consensus that the final theory does
not extend the principle of relativity to accelerating motion in any
interesting way. For an elaboration, see the later chapter, The
Relativity of Accelerated Motion.
You should treat what follows as interesting reports on Einstein's
intellectual biography. You may well find it hard to connect some of
the ideas to be laid out below with the final theory. |
The Starting Point
Einstein's first concrete steps on his pathway to general
relativity came in 1907 when he was commissioned by Johannes Stark to
write a review article on relativity theory
for Stark's journal Jahrbuch der Radioaktivitaet und Electronik.
The exercise was, apparently, quite straightforward. In his 1905 theory,
Einstein had offered a new account of space and time. Since the theories
of physics were all set in space and time, physicists needed to be assured
that these theories could be maintained; or, if not, shown how they should
be adjusted to fit with Einstein's new theory.

The exercise proceeded well.
Electrodynamics actually needed no adjustment. Einstein's 1905 theory of
relativity had been created to fit with the existing theory. The mechanics
of bodies required adjustments to the notions of energy, momentum and
mass. The most prominent of these was the famous equivalence E=mc2.
Einstein also sketched a relativistic treatment of thermodynamics, the
theory of heat and work.



Then came gravity. Newton's
celebrated theory of gravitation presumed instantaneous action at a
distance. The sun now exerts a gravitational force on the earth now
with a magnitude set by Newton's inverse square law. The key part was the
"now." If the sun were to move slightly, the resulting alteration in the
force it exerts on the earth would be felt by us instantaneously according
to Newtonian theory.


That means that Newton's theory depends upon a notion of absolute
simultaneity. A change there is felt here at the
same moment. However Einstein's 1905 theory had banished absolute
simultaneity from physics. Different observers would judge different pairs
of spatially separated events to be simultaneous. Newton's theory had to
be adjusted to accommodate this new relativity.
Adjusting Newton's Theory of Gravitation
The change needed was, apparently, straightforward. In the
revised theory, a change in the sun should not be felt here on earth
instantly, but only after a time lag of
around 8 1/3 minutes, the approximate time light takes to propagate from
the sun to the earth. Then absolute simultaneity would no longer be needed
in the theory.
This meant that Newton's theory needed to be adjusted to
look more like electrodynamics. In the latter theory, effects do not
propagate instantly in the electromagnetic field; they propagate in waves
at the speed of light. There were many ways to make the adjustments
Newton's theory needed. All of them produced very small changes in the
predictions of the theory. While one might not be sure precisely which of
the many adjustments was the right one to pick, there did not seem to be
any major problem. Rather the issue was a surfeit of
good solutions. Or so believed other leading thinkers of
Einstein's time, such as the great French mathematician, Henri Poincaré,
and the inventor of spacetime, Hermann Minkowski.
Einstein, however, did not see it that way. He examined
gravitation theories, modified to allow for a finite time of propagation
of effects, and found a result that aroused great
suspicions in him. In the modified theories, the distance fallen
by a body varies according to its sideways motion. In the simplest case,
the body would fall a shorter distance if it has some sideways velocity.

The differences in the distances
fallen were very small and not likely to be detectable in an
experiment. Nonetheless they bothered Einstein. They contradicted the
exact correctness of Galileo's old observation that all bodies fall alike,
even though the differences were far too small to be detectable by the
methods available to Galileo.
Other physicists of the time were aware of this effect,
but discounted it as too small to be of any concern. Einstein did not. It
meant that the way a body fell would depend on the energy of the body. We
can only guess now why that bothered Einstein
so much. It might be that Einstein imagined that a hot body, consisting of
many small atoms in thermal motion, might fall differently from a cold one
according to these theories.
Einstein was still a clerk in the Bern patent office in
1907. Yet he came to the extraordinary conclusion that an adequate theory
of gravitation could not be devised within
the confines of his existing theory of relativity.
"The Happiest Thought of My Life"
It was while pondering this problem that Einstein hit upon
what he later described as "the happiest thought of my life." If began
when he suddenly saw new significance in a commonplace of Newtonian
gravity. A body in free fall in Newtonian gravity does not
feel its own weight. This effect is very familiar to us now. We
have all watched space-walkers floating weightlessly outside their
capsules. They are in free fall above the earth, orbiting with their space
stations, and that free fall cancels their weight.

| This effect came about from an apparently
accidental agreement of two quantities in Newtonian theory: the
inertial mass of a body happens to equal its gravitational mass
exactly. Einstein now believed that this equality
could be no accident. He needed to find a gravitation theory in
which this equality is a necessity. |
The immediate outcome of this
reflection was Einstein's "principle of equivalence." It formed the basis
of the concluding Part V of his 1907 Jahrbuch article. There he
suggested that gravitation required an extension of special relativity
based on the principle of equivalence.
The Principle of Equivalence
There are very many formulations
of the principle of equivalence in the literature. Most of them pick up
directly on the idea of weightlessness in free fall. They assert that free
fall transforms away a gravitational field in some tiny volume of space.
While this is a common formulation of the principle in text books, it is
troubled. Free fall transforms away gross effects of gravitation. But, in
Einstein's final theory, it does not transform away the effects of
spacetime curvature. In that sense, free fall does not transform away
gravity in the final theory.
For an elaboration on these foundational issues, see The
Principle of Equivalence in the later chapter "The Philosophical
Significance of General Relativity: The Relativity of Accelerated Motion."
| Einstein later complained about this version of
the principle, objecting that one could not in general transform
away an arbitrary gravitational field over an extended region of
space. His original formulation and the one to which he adhered for
his entire life proceeded differently. He turned
around the original idea of free fall eradicating
gravitation. Acceleration can also produce a gravitational field. |
More specifically, Einstein took the case of special
relativity without gravitation. He now imagined a uniformly accelerated
observer, in relation to whom all free objects would accelerate. That
state of space found by the observer, Einstein asserted in his principle
of equivalence, is a homogeneous gravitational
field. In this case, uniform acceleration and homogeneous gravitation are
equivalent.
Einstein developed the idea in one of his best known
thought experiments. He asked us to imagine a physicist who awakens
in a box. Unknown to the physicist, the box is in a distant part
of the space of special relativity and is being accelerated uniformly in
one direction by the tug of some agent. If the physicist were to release
objects in the box, they would be left behind by the accelerating box;
they would move inertially, while the box accelerated. This figure shows
this for two bodies of different mass at rest and a third body that has a
horizontal inertial motion.

The physicist inside the box would find that the released
masses to accelerate in a direction opposite to the box's acceleration.
The physicist would judge there to be a field inside
the box pulling on all free bodies.

Now comes the key point. All bodies released by the
physicist would fall exactly alike, no matter what their mass or
composition. So the field found by the physicist inside the box would
manifest the signature property of a
gravitational field: it would accelerate all bodies exactly alike.
One might be tempted to say that the field inside the box
is just an "inertial field," some sort of fake gravitational field. Einstein's
assertion was otherwise. The field created by motion in the box
just is a full-blown, authentic homogeneous gravitational field.
- Principle of Equivalence
- The inertial effects inside a uniformly accelerated box in gravitation
free space are equivalent to those of a homogeneous gravitational field;
more tersely, uniform acceleration creates a homogeneous gravitational
field.
The equivalence just asserted may seem benign. It seems
just to codify an equivalence in the way bodies fall in two cases. In fact
the assertion is strong, for it asserts that the equivalence applies
to all processes, not just to the fall the bodies. That means
that it applies also to all processes involving fields, such as electric
and magnetic fields.
You will see why Einstein found this principle attractive.
His efforts to produce a relativistic theory of gravity had failed since
he could find no theory in which all bodies fell alike, no matter what
their mass or composition. The gravitational field delivered by the
principle of equivalence was assured to have this property. In particular,
the sideways motion of a body would have no effect on its rate of fall.
The field generated in this thought experiment did not have the defect of
the earlier theories.
Relativity of Inertia ("Mach's
Principle")
What also attracted Einstein in this analysis was that it
promised to remedy a defect he perceived in
both Newton's physics and in special relativity. In both, you will recall,
it is just a brute fact that certain motions are distinguished as
inertial. This, in Einstein's view, was worrisome. It was no better than
the original idea that there is an ether state of absolute rest. There
seemed to Einstein no good reason for why one state should be the absolute
rest state rather than another. Correspondingly, Einstein saw no good
reason for why some motions should be singled out as inertial and others
as accelerating.
In 1916, Einstein formulated this worry in a thought
experiment. He imagined two fluid bodies in a
distant part of space. These bodies, the reader quickly infers, are like
stars or planets, which form roughly spherical shapes under their own
gravity. Einstein further imagined that there is relative rotation between
the two bodies about the axis that joins them. This relative rotation is
verifiable by observers on each body, who can trace out the motion of the
other body. Each would judge the other to be rotating.

It can happen in ordinary Newtonian physics that one of
these bodies is not rotating with respect to an inertial frame and the
other one is. In that case, the second rotating body
will bulge but not the first. This effect arises on the earth. It
rotates about the axis of its north and south poles. It bulges slightly at
the equator as a result of centrifugal forces that seek to fling the
matter of the earth away from this axis.
It would be entirely unacceptable, Einstein now asserted,
were this to happen to two spheres in an otherwise empty space. For there
is no difference in the observable relations between the two spheres. Each
rotates with respect to the other. So why should just one bulge? The
supposition of Newton's absolute space or of inertial systems, Einstein
protested, was an inadequate explanation.
Einstein demanded something observable to make the difference.
 |
Einstein was an avid reader of the
physicist-philosopher Ernst Mach. In Mach's writings, Einstein had
found what seemed to be a solution to the problem. Mach seemed to be
proposing, Einstein thought, that the privileging of certain states
of motion is due to the distribution of
matter in the universe. Why is our frame of reference inertial? It
is because the stars are at rest in our frame. |
When we try to accelerate, we feel inertial
forces. These are the forces that make us dizzy when we spin in a
fun fair; or they are the forces that throw our coffee in the air when our
airplane hits an air pocket.
These forces, Einstein understood Mach to assert, arise
from an interaction between the mass of our body (and our coffee)
and all the other masses of the universe, distributed in the stars.
Einstein first called this idea the "relativity of inertia" and later, in
1918, "Mach's Principle."
In the case of Einstein's two fluid
spheres, the bulge of one of them would now be explained by the
fact that this bulging sphere was rotating with respect to all the other
masses of the universe, whereas the other sphere was not. That would be
the observable difference between the two fluid bodies.

Image sources:
https://www.nasa.gov/sites/default/files/images/283003main_solar_full.jpg
https://www.nasa.gov/sites/default/files/thumbnails/image/hubble_friday_08052016.jpg
This analysis was clearly inspired by Mach's famous
account of Newton's bucket experiment. Newton
had noted that water in a spinning bucket adopts a concave surface. The
concavity is a result, Newton urged, of its rotation with respect to
absolute space. No, Mach had responded several hundred years later, all
one has in the case of Newton's bucket in rotation with respect to the
stars. We cannot know anything more than what our direct observations tell
us. All they tell us is that these inertial forces arise when we
accelerate relative to the stars.
The weakness of this analysis is that there is no account
of how rotation with respect to distant masses could produce these
inertial forces. In 1907, Einstein hoped that
his emerging theory of gravity would provide the mechanism. It could then
satisfy Mach's Principle and, through it, generalize the principle of
relativity to acceleration. For in a theory that satisfies Mach's
Principle, no state of motion is intrinsically inertial or accelerating.
When we see something accelerating, it is not accelerating absolutely in
such a theory; it is merely accelerating with respect to the stars.
Preferred inertial motions need not enter into the account any more. All
motion, accelerated or inertial, would be relative.
To deliver this sort of account of inertial forces,
Einstein's theory would need to break down the strict division between
inertial and accelerated motion of his special theory of relativity. The principle
of equivalence promised to weaken this division. According to it,
whether the physicist in the box was to be judged accelerating or not
depended on your point of view. An inertial observer would judge the
physicist to be accelerating uniformly in a gravitation free space. The
physicist would judge him or herself to be unaccelerated in a
gravitational field. It was a first step towards generalizing the
principle of relativity to acceleration, Einstein believed.
Learning About Gravitation
By his own later judgment, Einstein did not, in the end,
find a theory that fully satisfied Mach's Principle. The immediate benefit
of his new principle of equivalence, however, was that it let Einstein
learn a lot about gravitation. For the principle delivered to Einstein one
special case of a gravitational field that, he believed, conformed with
relativity theory and in which all bodies truly fell alike. Einstein's program
of
research on gravity in the five years following 1907 was simply
to examine the properties of this one special case and to try to
generalize them to recover a full theory. His early hope was that the
generalization of the principle of relativity would somehow emerge in the
course of those investigations.
Gravitational Slowing of Clocks
Two properties of this special case of the gravitational
field were noteworthy. First, Einstein recognized that clocks
run at different rates in the box of his thought experiment
according to their location. A clock placed lower in the created field
runs slower.

Einstein immediately generalized that effect to all
gravitational fields. Clocks deeper in a gravitational field run slower. A
clock in the sun would run slower than one on
earth--if only we could have a clock in the sun without it being destroyed
by the heat of the sun. It turns out we can find clocks in the sun.
Radiating atoms radiate in very definite frequencies of light according to
which element they are. That means that they behave like little clocks.
Their running slower is manifested in a slight reddening of the light they
emit. Einstein computed an effect on the wavelength of sunlight of one
part in two million.
While Einstein did not use spacetime diagrams in 1907,
they provide an easy way to see that clocks run at different rates
according to their position when they accelerate in a Minkowski spacetime.
The effect is driven almost entirely by the relativity
of simultaneity.
| The spacetime diagram shows two clocks A and B
accelerating together towards the right in a Minkowski spacetime.
The numbers show the proper time elapsed along each clock's
worldline and thus the time each clock reads. The hypersurfaces of
simultaneity are those of the inertial
observer on the left of the figure. According to that
inertial observer, the two clocks run at the same speed, at least
for the initial portion of their acceleration. |

Now consider an observer who accelerates with the
rightmost "B" clock, that is, the clock higher up in the created field. As
the clock changes speed, that observer's hypersurfaces
of simultaneity will tilt so that the B observer will judge the A clock to
be lagging successively more behind. When B's clock reads 2, B will judge
the A clock to read 1; when B's clock reads 4, B will judge the A clock to
read 2. Overall, B will judge A's clock to be running at half the B
clock's speed. The effect, the figure shows, is entirely due to the
relativity of simultaneity.

The geometry of uniform acceleration in a Minkowski
spacetime turns out to be especially simple. The hypersurfaces of
simultaneity of an observer accelerating with the B clock turn out to
coincide with the hypersurfaces of simultaneity of an observer
accelerating with the A clock. Hence the observer
moving with clock A will agree that the A clock is running slower
and the B clock faster. When the A observer's clock reads 1, A will judge
B's clock to read 2. When the A observer's clock reads 2, A will judge B's
clock to read 4.
Gravitational Bending of Light
The second important effect pertained to light. An
unaccelerated observer finds that light propagates in a straight
line in the space of special relativity. Here, for example, is
such a light flash propagating across the box of Einstein's thought
experiment.

For the physicist accelerating with the box, however, the
light will be judged to fall, just like
everything else in the box. As a result, the physicist will find the
light's path to be bent downward by the gravitational field.

Einstein generalized this result to arbitrary
gravitational fields. This generalization enabled him to make one of the
most celebrated predictions of his theory. A ray of starlight
grazing the sun would be bent as the light fell into the sun's
gravitational field. This bending would be manifested as a displacement of
the star's apparent position in the sky and this displacement would be
visible at the time of a solar eclipse.
In 1907, Einstein had predicted the gravitational bending
of light. But he did not realize that it might actually be tested at the
time of a solar eclipse. After his 1907 Jahrbuch article,
Einstein's efforts were redirected towards the puzzle of the quantum. In
1911, however, he returned to theorize about gravity. He realized then
that his prediction of the gravitational bending of light could be tested
at a solar eclipse. He wrote another paper developing this idea
and also other aspects of his theory.
Einstein was keen to see this test undertaken. The
greatest difficulty was that it required a solar eclipse and that meant
that astronomers must place themselves precisely in its path. In 1913,
Einstein wrote to the American astronomer G. E. Hale asking whether the
test could be undertaken without an eclipse.

Hale responded that it could not. The brightness of the
sky near an uneclipsed sun is just too great.
In August 1914, there was a promising eclipse of the sun
that would be visible from the Crimea.
Einstein's colleague, the astronomer Erwin Freundlich, mounted an
expedition to the Crimea to observe and photograph the eclipse.
Unfortunately for Freundlich,
the First World War broke out. Since he was German, a citizen of an enemy
nation, the Russians interned him and confiscated his equipment.
Fortunately for Einstein, no
measurement was taken. Einstein's theory of 1914 was not yet the complete
general theory of relativity. In his earlier theory, there was no
curvature of ordinary space in the vicinity of the sun. As a result, as we
saw in another
chapter, his theory predicted the same deflection as Newtonian
gravitation theory (assuming light consists of massive corpuscles). It was
half the deflection predicted by the final theory. Had the test been
carried out successfully, it would have produced a result that
contradicted Einstein's earlier theory.
Gravitational Slowing of Light
In 1907, Einstein had also concluded that the speed
of light, and not just its direction, would be affected by the
gravitational field. The effect was closely connected with the
gravitational slowing of clocks and is almost entirely a consequence of
the relativity of simultaneity. One can see how it comes about with a
similar set of spacetime diagrams. The clocks A, A', B and B' all
accelerate uniformly in a Minkowski spacetime and in a way that ensures
that the distance from A to A' remains the same as from B to B'. A light
signal propagates from A to A' and a second light signal propagates from B
to B'.
The figure shows the hypersurfaces of simultaneity of an
inertial observer. Of course the inertial observer will judge the
two light signals to propagate at the same speed. That is just familiar
special relativity.
We notice also that, initially, the four clocks A, A', B,
B' run in synchrony according to the judgments of simultaneity of the
inertial observer. Hence using the readings of these clocks directly, we
will infer that the two light signals propagate at the same speed. In more
detail, we note that the distance from A to A' equals the distance from B
to B'; and each light signal takes the same time to traverse the distance.
Both light signals leave when the local clocks read 0 and arrive when the
local clocks read 3. Hence using these local clock
readings, we infer that the two light signals travel at the same speed.

Now consider how these processes are judged by an observer
who accelerates with the clocks. All that changes in the analysis that
follows is that we use different judgments of
simultaneity. That leads to the judgment of differing speeds for
the propagation of light.
Let us take the observer who accelerates with clock B.
That observer's hypersurfaces of simultaneity will tilt more and more as
clock B gains speed from the acceleration. This was the effect that led
observer B to judge that the A clock was running slower than the B clock.
This same tilting will lead observer B to judge that the AA' light signal
propagates at roughly half the speed of the
BB' light signal. Both signals traverse the same distance. However the the
AA' signal leaves A when the B clock reads 0 and arrives at A' then the B
clock reads 4. The BB' signal leaves B when the B clock reads 0 and
arrives at B' when the B clock reads a little over 2.

Recall that the judgments of simultaneity of accelerating
observers who move with the clocks agree, since they agree on the
hypersurfaces of simultaneity. So we can choose any one of the
accelerating observers and get the same outcome. Each of the accelerating
observers will judge the transit time for BB' to be roughly half that of
AA'. They will agree that light propagates slower on the left side of the
figure, that is, deeper in the created field.
Applying the principle of
equivalence, we now conclude that the same slowing manifests in a
gravitational field. A light signal deeper in the gravitational field at A
propagates slower than a light signal higher in the gravitational field at
B.
The conclusion that gravity slows the speed of light
caused Einstein some trouble with unkind
contemporary critics. Einstein had first based his theory of 1905
of the striking idea of the constancy of the speed of light, but he now
seemed to be retracting it.
By 1912, Einstein had developed all these ideas into a
fairly complete theory of static gravitational fields, that is
gravitational fields that do not vary with time and admit well defined
spaces. The most striking characteristic of the theory was that the intensity
of the gravitation field, the gravitational potential, was given
by the speed of light. So as one moved to different parts of space, the
intensity of the gravitational field would vary in concert with the
changes in the speed of light. As late as 1912, some five years after
Minkowski's work, Einstein was loath to use spacetime methods. While I
have developed the clock slowing and light slowing effects using spacetime
diagrams, Einstein did not do this. His method of analysis was algebraic.
He represented the processes by equations in which speeds and times
appeared as variables. He rarely if ever drew diagrams such as given
above.
What Einstein now needed was a way to extend
these results to the more general case of gravitational fields
that vary with time. That, it turned out, required Einstein to move well
beyond the mathematics he knew. Another thought experiment pointed the
way.
The Rotating Disk
If one has a circular disk at rest in some inertial
reference system in special relativity, the geometry of its surface is
Euclidean. It will be useful to spell out what that means in terms of the
outcomes of measuring operations. If the disk is ten feet in diameter,
then it means that we can lay 10 foot long rulers across a diameter.
Euclidean geometry tells us that the circumference is π x 10 feet, which
is about 31 feet. That means that we can traverse the full circumference
of the disk by laying 31 rulers around the
outer rim of the disk.
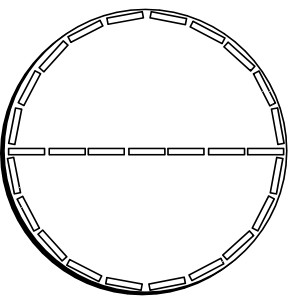
What if we have a disk of the same
diameter of 10 feet but in rapid uniform rotation with
respect to the first disk? Things will go rather differently. Assume
that this rotating disk is covered with foot long rulers that move
with it. These rulers are just like the ones that were used to
survey the non-rotating disk. (That means that an observer moving
with the rod on the rotating disk would find it to be identical to
one of the rulers used to survey the non-rotating disk.) What will
be the outcome of surveying the geometry of this rotating disk with
those rods?
An observer who is not rotating with the disk would judge all these
rulers to have shrunk in the direction of their motion. That means
that, according to this new observer, the surveying of the disk
would proceed differently. Ten rulers would still be needed to span
the diameter of the disk. Since the motion of the disk is
perpendicular to the rulers laid out along a diameter, the length of
these rulers would be unaffected by the rotation. That is not so for
the rulers laid along the circumference. They lie in the direction
of rapid motion. As a result, they shorten. More
rulers are needed to cover the full circumference of the
disk. |
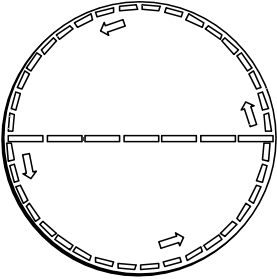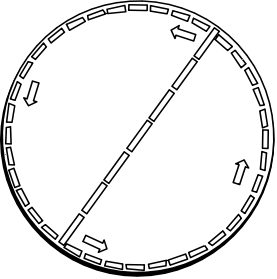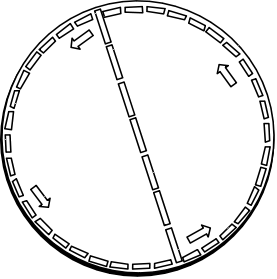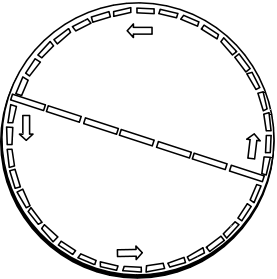
Thus we measure the circumference of the rotating disk to
be greater than 31 feet, the Euclidean value. In other words, we
find that the geometry of the disk is not Euclidean. The circumference of
the disk is more than the Euclidean value of π times its diameter.
The significance of this
thought experiment was great for Einstein. Through his principle of
equivalence, Einstein had found that linear acceleration produces a
gravitational field. Now he found that another sort of acceleration,
rotation, produces geometry that is not Euclidean.
Assembling the Pieces:
The "Entwurf" Paper of 1913
Einstein had all this in place by the summer
of 1912. He knew that gravitation could bend light and slow
clocks. He expected that the final theory would somehow involve
accelerations in a new way and that such accelerations came with a
breakdown of Euclidean geometry. He also knew that the natural arena in
which to conduct relativity theory is Minkowski's spacetime.
| Gravity
slows clocks and bends light. |
Uniform,
unidirectional acceleration produces a homogeneous gravitational
field. |
Rotational
acceleration leads to spaces with non-Euclidean Geometries. |
Spacetime
is the appropriate arena for relativity. |
|
 |
To us, the final step does not seem like such a
great leap. Assemble the pieces and infer that
gravitation is a curvature of spacetime! All that is needed is a
nice mathematical clothing to dress this idea.
For Einstein in 1912 it was far from easy. He first needed the
assistance of his mathematician friend Marcel Grossmann to find his
way in the new and difficult mathematics the theory required. |

Marcel Grossmann |
Grossmann visited the library and found a review article
on the "absolute differential calculus"
of Ricci and Levi-Civita from 1901. (We now call it "tensor calculus.") It
enabled the equations of a physical theory to be written in any coordinate
system. This, in Einstein's view, was just the mathematical instrument
needed, for Einstein had associated an extension of the principle of
relativity to acceleration with an expansion of the spacetime coordinate
systems of a theory.
The two collaborated on the paper shown opposite.
It is called, in translation, "Sketch [Entwurf] of a Generalized
Theory of Relativity and a Theory of Gravitation."
They divided the work. Grossmann, the
mathematician, developed the complicated mathematics, mostly
then unknown to physicists. This occupied the second part: "II.
Mathematical Part."
The physical reasoning in which the theory itself was developed was
to be written by Einstein in the first part: "I. Physical Part."
To a modern relativist, the paper is a little odd for the antiquated
notation Einstein and Grossmann used. However most
of the content is familiar. The spacetime of Minkowski is
generalized to embrace gravitational phenomena by allowing for what
we would now call curvature of the spacetime. The formalism of what
we now call "tensor calculus" is developed and used to state the
main results. The law of conservation of energy and momentum appears
in a form that is equivalent to that of the modern textbooks. |

|

|
Then comes the key question of the gravitational
field equations. Here things started well, at least in Grossmann's
mathematical part. From a mathematical perspective, the place to
start was the Riemann curvature tensor. It is the quantity that
measures the curvature of all the different sheets of spacetime.
Grossmann introduced it on the page opposite as the the "Christoffel
four-index-symbol of the first kind" (ik, lm). He
then performed the mathematical operation of contraction on it to
yield the expression Gim seen in the middle of
the page.
This quantity is almost the Einstein tensor. Grossmann is
so close to the modern Einstein field equations that one could now
scarcely imagine how the final steps could not be taken.
But they are not taken. One condition the new equations must satisfy
is that they must return Newtonian results for ordinary conditions.
For Newton's theory works extraordinarily well for the weak, static
gravitational fields of our solar system. The sentence highlighted
in red says:
"However it turns out the this tensor does not
reduce to the [Newtonian expression] Δφ in the case of
infinitely weak, static gravitational fields."
That is, Grossmann declared the equations under consideration not to
merge nicely back into Newton's theory in this essential case.
With that declaration, the paper turns from the road that was
leading directly to the Einstein field equations. |
With the catastrophic turn taken, Einstein took
up the search for gravitational field equations in his physical
part. He was guided by the few clues he had at hand: his earlier
results of 1907-1912 on static gravitational fields, the requirement
that the theory merge back into Newtonian theory and the requirement
of conservation of energy and momentum.
Einstein eventually found equations that he
believed adequate. They are complicated and have been given
no clear geometric meaning. Parts of them are spread over the page
opposite. If they look complicated to you, don't fret. That also was
the reaction of Einstein's contemporaries.
One simple equation of Newton's theory had been replace by ten,
non-linear, coupled equations of Einstein's theory. |

|
What Went Wrong?
Einstein took a series of bad
turnings and ended up with the wrong gravitational field
equations--not the celebrated Einstein equations that appear in all the
modern textbooks. He needed over two years of painful work first to
recognize that something had gone wrong and then to find the final
equations.
The precise causes that brought about
these wrong turnings remain a point of debate
in the history of general relativity literature. We can identify two
elements, however, that played a role in misleading Einstein.

|
First, in 1912 and 1913, Einstein had recognized
the need to employ a geometry of variable curvature in spacetime in
his theory of gravity. However he was convinced that this curvature
would not be manifested in the space-space slices of spacetime in
certain simple cases.
These were the cases of a static gravitational field and also of
very weak gravitational fields. These two cases combined is just the
circumstance identified by Grossmann as troublesome.
Both of them are realized in the gravitational field of the sun.
Einstein expected space around the sun to be exactly
Euclidean. Alas, as
we have seen, Einstein's final theory requires curvature in
the space-space slices even in this simple case. That meant that
Einstein and Grossmann could not accept the equations of the final
theory for they would entail a curvature of space when Einstein
believed there was none.
|
Second, Einstein used a different style of theorizing to
the one largely used in these chapters. Here, we have used a geometrical
approach, emphasizing the picturing of gravitational effects in geometric
diagrams. Einstein, however, labeled events in spacetime with arbitrarily
coordinate numbers and expressed all his results in terms of equations
relating these coordinates. Einstein knew that this labeling of spacetime
events with coordinates was purely arbitrary and that all his results had
to be independent of the particular coordinate
system used. However knowing this in the abstract and carrying through the
demand in all details are two different things. Einstein's "Entwurf" field
equations applied only to specialized sets of coordinate systems. He
called them "adapted." By his own later admission, Einstein had found it
hard to purge his coordinate systems of independent reality.
One of the low points in his struggle with coordinate
systems came when Einstein used an ingenious argument--the "hole
argument"--to show that gravitational field equations like the
ones of his final theory are inadmissible on physical grounds. While the
hole argument did not warrant that conclusion, it has been rehabilitated
in recent work in philosophy of space of time, where it now lives a good
life.
For an elaboration, see the later chapter "The
Philosophical Significance of General Relativity: The Hole Argument."
(See also, "The
Hole Argument." Stanford Encyclopedia of Philosophy.)
The Zurich Notebook
The time of Einstein's collaboration with
Grossmann that led up to the "Entwurf" paper is the decisive period
for the discovery of general relativity. For it is when Einstein
takes the hunches and results of his earlier speculations and molds
them into the theoretical framework of general relativity. It would
be wonderful if we could look over Einstein's
shoulder during this period and watch him work. We would
see the creation of general relativity. Of course, 1912 and 1913 are
now in the past.
We can do something almost as good. The private calculations
Einstein made during this time have survived. The pages of the
Zurich Notebook enable us to watch the steps Einstein took, from the
earliest moment when he connected gravitation with spacetime
curvature, through the evaluation and rejection of his later field
equations, on to the equations of his "Entwurf" theory. |

|
For a more detailed glimpse into Einstein's notebook, see
"A
Peek into Einstein's Zurich Notebook." on my Goodies
page. Here's one page on which Einstein writes down the Riemann curvature
tensor for the first time and finds it hard to see how it can be used in
his gravitational field equations.

The notebook has many wonderful insights into the detailed
steps of Einstein's work; and there are still pages whose content eludes
us. Each is a little puzzle for us solve. One remarkable page that
defeated me was solved by Tilman Sauer. It shows Einstein
playing with the key ideas of his new theory in a way that
does not persist into later publication.

It will not be at all obvious what Einstein is computing
on the right hand side of this page. At least it was not to us for a long
time. So let me tell you what Einstein computes.
In general relativity, a body in free fall traces
out a geodesic of the spacetime. That is, it follows a trajectory of
extremal proper time.
There is a result which looks unnervingly close to this in
ordinary classical physics. Take a curved surface. Have
body that can move freely in it, except that it is not allowed to
leave the surface. An example is shown opposite: a particle is
captured by the curved surface of a cup. While the body skims over
the surface of the cup, what curve is traced out in the surface of
the cup?
It is a geodesic of cup's surface! That is, it traces a curve of
shortest spatial length.
That fact is what Einstein deduces on this page. |

|
The result is so close to the central idea of Einstein's
general theory of relativity that one has to look closely to see how the
two differ:
| Classical
physics |
General
relativity |
| A
mass moves freely in space, except that it is constrained to a
two-dimensional surface in the three-dimensional space. |
A
mass moves freely in spacetime. That is, it is in free fall, so
that gravity acts on it through the curvature of spacetime. |
| Its
spatial trajectory is a geodesic of the two-dimensional surface.
That is, it traces of curve of shortest length in the surface. |
Its
spacetime trajectory is a geodesic of the spacetime. That is, it
traces a curve of extremal spacetime interval in spacetime. |
November 1915: The Race to the
Finish
With the publication of the "Entwurf" paper in mid 1913,
Einstein felt that the major work on the theory was done. Only the details
needed to be clarified. The feeling did not last. As the months and years
passed. Einstein worked harder and harder to
convince himself that all was well with a theory that was misshapen in its
fundamental equations.
In the summer and fall of 1915, the clues
that his old theory was wrong mounted. He knew that his theory of
1913 did not accommodate the anomalous motion of Mercury. He then found
that it did not extend the relativity of motion to rotation. Finally, he
found that an improved and much more sophisticated development of the
theory of late 1914 did not demonstrate its uniqueness, as he then
believed.
In mounting despair and desperation to save his theory, he
returned to the thinking of 1912 and 1913. He was mistaken, he saw, to
restrict his theory only to the special "adapted" coordinate systems of
the "Entwurf" theory. He needed a theory that would work in as many
coordinate systems as possible. Ideally it would work in all coordinate
systems. That is, it would be "generally covariant."
What followed was the most exhausting and exhilarating
month of Einstein's life. He sent the Prussian academy bulletins on his
reformulated theory, one per week, each correcting errors and
incompleteness of the previous bulletins. What no doubt lent special
urgency to this extraordinary behavior was the fact that David
Hilbert, the greatest mathematician of the era, had also become
interested in the theory and had started the project of rewriting the
gravitational field equations of Einstein's old "Entwurf" theory in a
mathematically more elegant formulation.
The first communication was sent on November
4 and was written as it if was the last.

It was not. The following week, November
11, Einstein sent a correction.

And the following week, November 18,
a jubilant Einstein communicated the remarkable news that his newly formed
theory accounted for the anomalous motion of Mercury. ("Explanation of the
perihelion motion of Mercury by the general theory of relativity.")

The field equations of the theory were still not quite
right. It was only in the fourth communication of November
25 that the final equations appeared.

Here are those equations as he published them for the
first time on 25 November 1915.
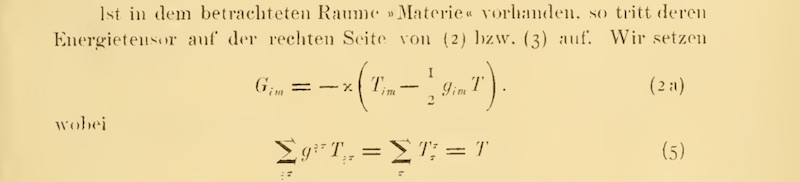
Here he writes them later in the simple case of a matter
free spacetime:

What You Should Know
- What first led Einstein to work on what became his general theory of
relativity.
- The principle of equivalence
- How Einstein used it to infer the properties of gravitational fields.
- The relativity of inertia.
- Einstein's transition to the mathematics of spacetime curvature.
Copyright John D. Norton. February 2001;
January 2, 2007, February 15, August 23, October 16, 27, 2008; February
5, 19, 2010. Minor edits February 26, 2013. More December 29, 2015.
January 15, February 27, 2017. LInks added November 16,
2019. February 4, 2022.