
https://en.wikipedia.org/wiki/File:Full_featured_double_rainbow_at_Savonlinna_1000px.jpg
| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Related document: Technical Appendix
Ontology is the study of what exists. The most common problem is to decide what is real and what is not. Is your reflection in the mirror real? Are mirages in the desert real? Are rainbows real? All are cases in which there seems to be a real thing in the world. However on closer examination we find that none is a real thing, or at least none has an independent existence. Mirages and rainbows arise from anomalies in the atmosphere redirecting light to our eyes in misleading ways. Your mirror reflection exists and ceases to exists exactly when you do.

https://en.wikipedia.org/wiki/File:Full_featured_double_rainbow_at_Savonlinna_1000px.jpg
The ontology of space and time asks similar questions about the reality of certain spatiotemporal aspects of the world. There is a popular view that "relativity" has somehow established the unreality of things to do with space and time that we formerly regarded as real. It is true for special relativity. We naively think that it makes sense to say whether something moves or not; and Newtonian physics enshrined the idea in its foundations. In establishing the relativity of inertial motion, Einstein eliminated absolute rest from physics.
However special relativity fell short of the slogan "All motion is relative." For acceleration remains absolute in special relativity. As we have seen in an earlier chapter, Einstein's project in seeking a general theory of relativity was to continue this relativization. If he could extend the principle of relativity to all motion, he would eliminate this vestige of the absoluteness of motion.
Einstein repeatedly claimed success in this project. However whether he did succeed remains at best disputed. In my view he did not succeed in this specific goal. That, of course, does not impugn Einstein's theory. It remains today our best theory of space, time and gravity. Einstein did, however, succeed in a related ontological goal: he established that his spacetime coordinate systems have no independent reality. That may at first seem obvious. However it was not so easy to grasp the full import of this lack of independent reality. We shall see that it was a hard won insight by Einstein. The insight lives on. In its modern reformulation, Einstein's analysis is a refutation of a particular form of spacetime substantivalism: the view that space is a substance.
This chapter will explain and develop these ideas. Einstein's views are easy to skim and, on a first quick reading, they look quite cogent. Closer reading, however, shows that it is hard to fit all the pieces together in a way that fits with Einstein's claims. As a result, Einstein's claims have become a subject of much contention. I will not try to survey the wide range of different viewpoints. That would require an unwieldy narrative. Rather I will lay out what I find to be the clearest pathway through this episode.
Readers interested in a survey of the range of viewpoints will find it in my "General Covariance and the Foundations of General Relativity: Eight Decades of Dispute," Reports on Progress in Physics, 56 (1993), pp.791-858.
The founding debate in the modern literature derives from Newton's masterful Principia Mathematica. The modern debates are framed by his ideas and the reaction of 17th century thinkers to them. Newton introduced the idea of the absoluteness of space and time when he declared in his Principia (Book 1 Scholium to the Definitions)
| "I.
Absolute, true, and mathematical time, of itself, and from its own
nature flows equably without regard to anything external, and by
another name is called duration: relative, apparent, and common
time, is some sensible and external (whether accurate or
unequable) measure of duration by the means of motion, which is
commonly used instead of true time; such as an hour, a day, a
month, a year. II. Absolute space, in its own nature, without regard to anything external, remains always similar and immovable. Relative space is some movable dimension or measure of the absolute spaces; which our senses determine by its position to bodies; and which is vulgarly taken for immovable space ; such is the dimension of a subterraneous, an aereal, or celestial space, determined by its position in respect of the earth." |
 Frontispiece from the 1846 American edition of Principia, New York: Daniel Adee. |
The central idea is that absolute space and time have an existence independent of any thing or any occurrence in the world. Moreover, absolute space remains at rest: it provides our physical theories with an absolute notion of motion or its absence.
Newton was disputed famously in his lifetime by Leibniz, in a correspondence with Newton's spokesman, Samuel Clarke. Leibniz articulated a relationist conception of space and time, which remains the traditional counterpoint to Newtonian absoluteness. He asserted:
"As
for my own opinion, I have said more than once, that I hold space to be
something merely relative, as time is, that I hold it to be an order of
coexistences, as time is an order of successions."
(Third letter to Clarke)
In more modern language, Leibniz asserts that there are
things related spatially, but there is no space;
and there are events related temporally, but there is no time. For
example--my example--the sun and planets do not inhabit a space. Rather
they are bodies that stand in spatial relations: the earth is this far
from the sun; and this far from the moon; and this far from Venus; and so
on. This list exhausts all the spatial facts in the planetary system.
There no additional thing, "space." Similarly, the planets do not move
about in time. Rather one particular configuration of spatial relations is
succeeded by another and then another. This succession exhausts all the
temporal facts of the planetary system. There is no additional thing,
"time."

"Mitchels solar system (c.1846)"
http://www.tablespace.net/maps2/index.html
This relationist conception of space and time was later applied by Ernst Mach in his critique of Newton's ideas of space and time. He wrote:
| "When
we say that a body K alters its direction and velocity solely
through the influence of another body K', we have asserted a
conception that it is impossible to come at unless other bodies A,
B, C. . . . are present with reference to which the motion of the
body K has been estimated. In reality, therefore, we are simply
cognisant of a relation of the body K to A, B, C. . . . If now we
suddenly neglect A, B, C. . . . and attempt to speak of the
deportment of the body K in absolute space, we implicate ourselves
in a twofold error. In the first place, we cannot know how K would
act in the absence of A, B, C . . . . ; and in the second
place, every means would be wanting of forming a judgment of the
behaviour of K and of putting to the test what we had
predicated,-- which latter therefore would be bereft of all
scientific significance." Ernst Mach, Science of Mechanics. 4th ed. Chicago: Open Court, 1919, pp. 229-30. |
 Frontispiece of Science of Mechanics, 4th ed, 1919 |
In 1905, Einstein was still a patent clerk. Flushed with the success of his special theory of relativity, he was eager to press on. In 1907, as we saw in an earlier chapter, he was ready to press on toward the goal of a truly general theory of relativity. Einstein made clear in his first speculative steps towards this goal that he sought an extension of the principle of relativity from inertial motion to all motion. He set out his goal in the opening words of his first publication in 1907 of research ideas that would lead to the completed general theory of relativity eight years later:
| "So
far we have applied the principle of relativity, that is, the
positing of the independence of the laws of nature from the state
of motion of the reference system, only to acceleration free
reference systems. Is it possible that the principle of relativity
holds also for systems that accelerate relative to each other?"
A. Einstein, "Über das Relativitätsprinzip und die aus demselben gezogenen Folgerungen," Jahrbuch der Radioaktivität und Elektronik 4 (1907): 411-462, on p. 454." |

|
Einstein's program had clear relationist sympathies. Writing in 1913, midway through his development of general relativity, he proclaimed:
"To
talk of the motion and therefore also acceleration of a body A in itself
has no meaning. One can only speak of the motion or acceleration of a body
A relative to other bodies B, C etc. What holds in kinematic relation for
acceleration ought also to hold for the inertial resistance, with which
bodies oppose acceleration . . ."
A. Einstein, "Zum gegenwärtigen Stand des
Gravitationsproblems." Physikalische Zeitschrift 14
(1913): 1249-1262, on p. 1260.
Here Einstein's formulation is remarkably close to the relationist conception we saw above from Ernst Mach. Einstein was an avid reader of Mach's writings and commended him for his critique of Newton's conceptions of absolute space and time.
By 1916, the general theory of relativity was complete and Einstein was confident that he had succeeded in extending the relativity of motion to acceleration. However his formulation of just what that meant was oblique. Here is a compact version of it from his 1919 popular article "What is the the Theory of Relativity," written for the Times of London (November 29, 1919):
"Should the independence of physical laws of the state of motion of the coordinate system be restricted to the uniform translatory motion of coordinate systems in respect to each other? What has nature to do with our coordinate systems and their state of motion? If it is necessary for the purpose of describing nature, to make use of a coordinate system arbitrarily introduced by us, then the choice of its state of motion ought to be subject to no restriction; the laws ought to be entirely independent of this choice (general principle of relativity)."
Here the general principle of relativity has become a statement involving "arbitrary coordinate systems." In retrospect, it now seems clear that Einstein had redefined what it would be for a theory to satisfy a generalized principle of relativity. The original idea in the case of the special theory was detailed in a very early chapter here. It is that no experiment can reveal our uniform motion. All uniform motions are experimentally indistinguishable. If that special principle is to extend to acceleration, we expect a theory to assure us that no experiment can reveal our acceleration. All motions--uniform and accelerated--would be experimentally indistinguishable.
However a coordinate system is just a way of assigning numbers to events in space and time. (More on this below.) It seems a truism that we can use any such system we like. We could always do that, even in Newtonian theory, as long as we keep careful track of just which system we are using to assign the numbers. How are we to connect the observational indistinguishability of the original special principle with this freedom of choice of coordinate systems?
For Einstein, the connection between the two had been there from the beginning. To see it, we need to pay special attention to how he formulated the original principle of relativity of the special theory. It was a continuation of that particular way of formulating the principle that led Einstein to his later version of the general principle of relativity. The key fact to be noted is that Einstein used coordinate systems as surrogates for states of motion. Using their surrogacy, he expressed the principle of relativity in terms of the form that the laws of physics take when written in those coordinate systems.
Here is how it worked.
We originally formulated the principle of relativity of special relativity in terms of inertial frames of reference. These consist of a physical systems of connected rods in a state of uniform inertial motion to which like constituted, synchronized clocks are attached.
It is a straightforward matter to use such a frame of reference to assign space and time coordinates to events. In case the grid of rods is laid out in a square lattice as shown, then we pick one node as the origin to be assigned zero spatial coordinates. Then we pick out three directions perpendicular to each other and aligned with the rods. These become the x, y and z axes. Coordinates values are assigned using the distances measured by the rods. Points one, two and three rod lengths along the x axis are assigned x coordinates 1, 2, and 3. The system is repeated for the y and z axes. Here is how it looks:
A similar strategy allows us to assign a time coordinate t to events. The time coordinate for an event is just the time read by the clock coincident with the event.
What results is the coordinate system for space and time used most commonly in special relativity. When applied to spacetime, the coordinate system looks like this:
These coordinate systems became for Einstein surrogates for the frames of reference. The surrogacy is unproblematic as long as we remember that these are specially chosen coordinates. The spatial coordinates x, y, z correspond to the results of measurements with rods at rest in the inertial frame of reference. The time coordinate t corresponds to time measurements taken by synchronized clocks at rest in the frame of reference. An easy short-hand to describe this special character is that these coordinates have "metrical significance"--they arise directly through measurements.
To see the relativity of inertial motion, we need to
introduce inertial frames of reference in relative motion. Each frame will
have its own metrically significant coordinate systems. We can transform
between them, much as we can translate a text in one language
into another. If we know the coordinates of some event, in one coordinate
system, Einstein demonstrated that we can find the coordinates of that
same event in another frame of reference by means the of the rules
we now know as the "Lorentz transformation."
Let us look at how the equations appeared in Einstein's original 1905 paper. Below I will display the equations, but without any need for a reader to grasp their full content. All that matters is a very particular aspect of the transformation Einstein describes.
| Start with some coordinate system, x, y, z and t
adapted to one inertial frame of reference. Now consider another inertial frame of reference that moves at speed v in the x-direction of this frame. The Lorentz transformation equations tell us how the coordinates of this new inertial frame of reference--τ for time, ξ, η and ζ for space--are to be assigned to events in space and time, given some specific t, x, y and z. Here is how the transformation first appeared in Einstein's original 1905 paper. (In Einstein's original work of 1905, he used "V" for the speed of light instead of the now familiar "c.") |
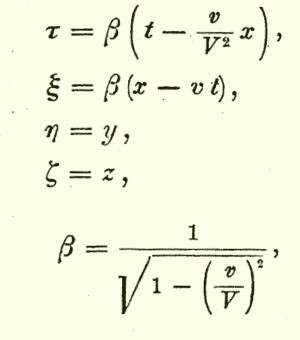 |
With this transformation in place, Einstein now turned to giving a formal expression for the satisfaction of the principle of relativity. His informal statement is that the laws of nature are the same in all inertial frames of reference. This sameness will be expressed as a formal condition on the way the laws of nature are written. By "formal" I do mean that the condition pertains directly to how the equations expressing the laws look when written down in symbols on the page.
Take the laws of Maxwell's electrodynamics. In his
original paper, Einstein writes two of the principal equations
of Maxwell's electrodynamics in the coordinate system t, x, y, z,
as follows. Again--the content of the equations will not be the issue. All
that matters is that you scan over the equations and see that they have
the coordinates x, y, z, t in them and the electric and magnetic field
quantities X, Y, Z, L, M, N.

Einstein applied the Lorentz transformation to find how the equations of Maxwell's theory would be expressed in the new coordinate system, τ, ξ, η and ζ. He found:
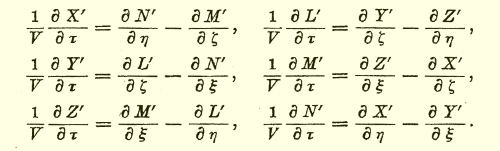
The essential point is that the transformed set of equations is just like the original. All that has changed is that there have been systematic replacements of the "old" quantities t, x, y, z, X, Y, Z, L, M, N by their "new" correlates, τ, ξ, η, ζ, X', Y', Z', L', M', N'. This animation shows that the form of the equations is unchanged:

When the laws of a theory retain their form when the quantities are transformed by the Lorentz transformation, the theory has the property of "Lorentz covariance."
This property of Lorentz covariance gives Einstein the relativity of inertial motion. For imagine that that there is some configuration of electric and magnetic fields X, Y, Z, L, M, N in the old t, x, y, z coordinate system. Maxwell's electrodynamics allows that configuration simply because the configuration satisfies Maxwell's equations. We can now see that a perfect clone of this configuration is possible in the new inertial frame of reference. We just re-express the original configuration in terms of τ, ξ, η, ζ, X', Y', Z', L', M', N' and we are assured that this new configuration is also allowed by Maxwell's equations.
That is, Lorentz covariance assures us that anything that can happen in the first inertial frame of reference can also happen in the second. That assures us that any experiment we can do in electrodynamics in one inertial frame of reference can be replicated exactly alike in any other inertial frame of reference. And that just means that the principle of relativity of inertial motion is satisfied.
 in t, x, y, z, X, Y, Z, L, M, N |
 in τ, ξ, η, ζ, X', Y', Z', L', M', N' |
Image:https://commons.wikimedia.org/wiki/File:Induction_experiment.png
Here is Einstein's terse statement of this formulation from 1940:
"The
content of the restricted relativity theory can accordingly be
summarized in one sentence: all natural laws must be so conditioned that
they are covariant with respect to Lorentz transformations."
From "The Fundaments of Theoretical Physics"
in Ideas and Opinions.
So far, all is well. This connection between the formal condition of Lorentz covariance and the physical principle of the relativity of inertial motion works. However its success depends on a restriction to a quite specific set of coordinate systems. Those related by the Lorentz transformation have the special property that space and time manifest in exactly the same way in each. More informally, space and time look exactly the same, in all their aspects, when described any of these special coordinate systems.
In later work, this fact about the Lorentz transformation is expressed by describing the transformation as a "symmetry transformation" or more fully "a symmetry of space and time." That is, it is a mapping that leaves space and time unchanged.
To help fix the idea, a simpler and more familiar example are the symmetries of an ordinary Euclidean space. They are translations and rotations. That is, a Euclidean space is the same if we move to a new location; and the same if rotate our view. We can re-express this in coordinate terms. Lay out some coordinate system in the Euclidean space. All properties of the space described in that coordinate system reappear identically if we move ("translate") the whole coordinate system to another part of the space; also if we rotate the coordinate system by any angle.
This idea of symmetry is THE ESSENTIAL NOTION for realizing a principle of relativity. It is present in special relativity. We shall see, however, that it is missing when we move on to general relativity.
The principle of relativity of inertial motion is captured formally by the Lorentz covariance of physical laws: the laws retain their form when we Lorentz transform between different coordinate systems. What if we move to a larger group of transformations among a bigger set of coordinate systems? They are loosely called "general transformations." These transformations will include those that relate coordinate systems adapted to inertial frames of reference to coordinate systems adapted to accelerating frames of reference. If the laws of physics remain unchanged in form when we apply these general transformation, we have extended Lorentz covariance to general covariance. Then, Einstein asserted, we have generalized the principle of relativity to accelerated motion.
 |
Here is how Einstein formulated the
idea in his major, 1916 review article, written just after the
completion of the general theory of relativity. Einstein
points out that his considerations lead coordinates to lose their
direct metrical significance. He continues |
The simple idea is that
general relativity of motion = general covariance
It is masked behind a technical
qualification. "All imaginable" coordinate sytems leads
us to far more transformations than are needed for expressing the general
relativity of motion. While some transformations will be surrogates for
shifts from unaccelerated to accelerating frames of reference, others will
not. The simplest of these other cases are transformations that merely
switch around the spatial coordinates but without affecting the time
coordinate at all. Consider, for example, a coordinate transformation that
just swaps the spatial x and y coordinates of events. There is no sense of
a change of state of motion, but we have introduced a new coordinate
system.
It is not immediately clear how Einstein intended this simple idea to be implemented. His principle of equivalence, however, provided a quite concrete illustration of it.
Clocks deeper in the induced gravitational field within an accelerating box run slower |
In an earlier chapter, we have already seen the principle as central to Einstein's heuristics in his discovery of general relativity. If we start in a gravitation free space and accelerate uniformly in a fixed direction, then free bodies in our neighborhood will fall with uniform acceleration. They fall just as if they are in a gravitational field. Einstein's principle of equivalence removed the "just as if." They are, it asserts, really in a gravitational field, even if one of a special character. The principle provided Einstein with a single example of a relativistically well-behaved gravitational field. The early years of Einstein's work on general relativity, starting in 1907, was focused on this special case of the gravitational field. He examined its properties in detail and sought a more general theory merely by generalizing these properties. |
This heuristic value of the principle obscured what was for Einstein the foundational significance of the principle. It was Einstein's first step towards a generalized principle of relativity.
Here is the most careful and complete statement of the
principle that I have found. It came in a relatively unknown paper by
Einstein from 1916.
"Ueber Friedrich Kottlers Abhandlung 'Ueber Einstein's
Aquivalenzhypothese und die Gravitation."' Annalen der Physik 51
(19i6), pp. 639-642. ("On Friedrich Kottler's paper 'On Einstein's
hypothesis of equivalence and gravitation.") Translation from "What
was Einstein's Principle of Equivalence?" Studies in History
and Philosophy of Science, 16 (1985), pp. 203-246; reprinted in
D. Howard and J. Stachel (eds.), Einstein and the History of
General Relativity: Einstein Studies Vol. I, Boston: Birkhauser,
1989, pp.5-47.
"Principle
of Equivalence. Starting from this limiting case of the special
theory of relativity, one can ask oneself whether an observer, uniformly
accelerated relative to [inertial coordinate sytem] K in the region
considered, must understand his condition as accelerated, or whether there
remains a point of view for him, in accord with the (approximately) known
laws of nature, by which he can interpret his condition as "rest."
Expressed more precisely: do the laws of nature, known to a certain
approximation, allow us to consider a reference system K' as at rest, if
it is accelerated uniformly with respect to K?
Or somewhat more generally: Can the principle of relativity be extended
also to reference systems, which are (uniformly) accelerated relative to
one another?
The answer runs: As far as we really know the laws of nature, nothing
stops us from considering the system K' as at rest, if we assume the
presence of a gravitational field (homogeneous in the first approximation)
relative to K'; for all bodies fall with the same acceleration independent
of their physical nature in a homogeneous gravitational field as well as
with respect to our system K'.
The assumption that one may treat K' as at rest in all strictness without
any laws of nature not being fulfilled with respect to K', I call the
"principle of equivalence." "
The principle extends the set of coordinate systems under consideration from those adapted to inertial frames of reference in special relativity to include those adapted to uniformly accelerating frames of reference. The transformations under consideration now include those that relate these inertial coordinate systems to uniformly accelerating coordinate systems. The extension of the covariance of Einstein's formulations to include these last transformations was regarded by Einstein as an intermediate on the way to full general covariance. He remarked in this same 1916 paper in emphasized text:
"The requirement of general covariance of equations embraces the principle of equivalence as a quite special case."
This extended covariance meant for Einstein that "one may treat [uniformly accelerating coordinate system] K' as at rest in all strictness." That is, the principle has extended the relativity of inertial motion
| Some figures will help us see more clearly what Einstein is claiming. Consider his two coordinate systems K and K'. The first system K is adapted to an inertial frame of reference and has coordinates T, X, Y and Z. The coordinate system K' is adapted to a uniformly accelerating frame of reference that accelerated with constant acceleration g in the +x direction of K. For simplicity, we will consider only small extensions of spacetime and small accelerations, so that relations between the two coordinate system are Newtonian, near enough. This is a simplification Einstein used himself in his 1911 exposition of the principle of equivalence, "On the Influence of Gravitation on the Propagation of Light." | For those who want the equation relating the two
coordinate systems, they are just t = T x = X - (1/2)gT2 y = Y z = Z The Technical Appendix has a more complete representation of the transformation to a uniformly accelerating frame of reference in special relativity. |
| Here is the inertial
coordinate system K. The Y and Z coordinate axes are not
shown since they do not play a role in the analysis. A free body in it remains at rest, as indicated by the vertical bold line. |
| Here is how the uniformly accelerating coordinate system K' relates to K. |
| We can redraw the
figure so that the t axis of the uniformly accelerating coordinate
system is vertical. This gives us the view of someone moving with
the uniformly accelerating frame of reference. The free body is accelerated in the -x direction with acceleration g. |
| On the authority of the principle of equivalence,
Einstein assures us, the observer moving with the accelerating frame
of reference does not need to understand the -x directed
acceleration as due to the acceleration of the observer. The
observer can consider the observer's state as "at rest" and the
motion of the free body as due to the presence of a homogeneous
gravitational field, acting in the -x direction. |
To implement Einstein's claim that the principle of equivalence is a covariance principle, we need to see how it can be used to secure the sameness of form of physical laws. An applicable law is the one that governs the inertial motion in special relativity of the free body shown in the figures.
In the inertial coordinate system K, the applicable law just says that the body is unaccelerated:
Acceleration = 0
That is, if you want the
formulae:
d2x/dt2 = 0 d2y/dt2
= 0 d2y/dt2 = 0
In the uniformly accelerating coordinate system, the corresponding law says that the body has constant, non-zero acceleration:
Acceleration = constant ≠ 0
That is, if you want the
formulae:
d2x/dt2 = -g d2y/dt2
= 0 d2y/dt2 = 0
These two expressions can be combined into one if we allow that the constant can equal zero and also may not equal zero. The the law governing the motion of the body in both coordinate systems K and K' is:
Acceleration = constant
We have secured the result Einstein sought. The principle of equivalence has led us to expand the coordinate systems we use to describe the motion of bodies in special relativity. It does it in a way that leaves the form of the governing law unchanged. That is, we have extended the covariance of the theory to include uniform acceleration. This for Einstein extends the principle of relativity to acceleration.
The principle of equivalence, in Einstein's formulation as sketched above, is a covariance principle. However it is not a relativity principle. That is, it is not if the term "relativity principle" is to have the same meaning as it has in special relativity. There the key idea was that principle of relativity of inertial motion eliminated absolute rest since the principle rendered absolute rest unobservable and inaccessible to all experimental determination.
In an earlier chapter, the principle of relativity of inertial motion and some of its important consequences were summarized as:
Principle
of Relativity: The laws of physics are the same in all inertial frames
of reference.
It follows that:
Absolute motion cannot appear in any law of physics.
All experiments run the same in all inertial frames of reference.
No experiment can reveal the absolute motion of the observer.
The principle of equivalence, in Einstein's recounting, is supposed now to eliminate the distinctive status of inertial motion. For it is supposed to be extending the relativity of motion from inertial motion to accelerated motion. However inertial and accelerated motions remain distinguishable absolutely. That is, if we are in an inertial frame of reference, we will find free bodies to move uniformly in straight lines. If, however, we are in a uniformly accelerated frame of reference, we will find free bodies to accelerate in conformity with motions produced by a homogeneous gravitational field.
These last remarks describe an experiment we can do to determine if our frame of reference is inertial or uniformly accelerated: just observe the motion of free bodies. Einstein said that we can treat the accelerated frame of reference as "at rest." Whatever he may have meant by this, it is not enough to give us the observational equivalence of inertial motion and accelerated motion.
| More precisely the difference is this. In inertial coordinate systems free bodies move such that their x, y and z coordinates are linear functions of the time coordinate t. In this sense they are straight lines in spacetime. In the uniformly accelerating coordinate systems, these x, y and z coordinates vary with t and t2. In this sense they are parabolas in spacetime. | A more abstract way to make the same point is this. Relativity principles are implemented by symmetry transformations, as described above. A Lorentz transformation is a symmetry of a Minkowski spacetime. The transformation from inertial to accelerated coordinate systems is not a symmetry of the Minkowski spacetime. For to be a symmetry, space and time would have to manifest in exactly the same way in the coordinate systems linked by the symmetry transformation. The transformation from inertial coordinate systems to uniformly accelerated coordinate systems fails to achieve this. The structure of space and time is plumbed by the motions of free bodies. These motions are different in the two cases. |
Here I have focused on what the principle of equivalence is not. However it does provide something. In an earlier chapter, I described how Einstein used it repeatedly to generate results about gravity that brought him closer to the final general theory. Perhaps the most import idea is brought was this. The Minkowski spacetime of special relativity is not to be thought of as the gravitation-free case. Rather, it is just a special case of the gravitational field. To see that, we do nothing to the spacetime. We merely accelerate and find that a homogeneous gravitational field manifests around us. This fact will eventually lead to the idea that the geometrical structures that make up Minkowski spacetime are all that is needed for a theory of gravity. The idea is implemented in general relativity by making special relativity the special case of a flat spacetime. General relativity covers the cases in which the spacetime is no longer flat and more varied gravitational phenomena appear.
The principle of equivalent describes one expansion of the covariance of special relativity. Einstein's interest was in a much greater expansion. He sought a theory whose covariance transformations connect all imaginable systems of coordinates (to use his expression). For these transformations would include those associated with all different types of accelerated motion, such an non-uniform acceleration in one direction or rotational motions.
However the expansion of the covariance does not solve the problem just sketched. The same objection applies to other transformation. If we have transformations that set our frame of reference and its coordinate systems into rotation, then the absolute fact of rotation will manifest in effects arising from centrifugal and Coriolis forces.
To see see that this problem is not solved by further expansion of the covariance of the theory, we should look more closely at what it takes to introduce arbitrary coordinate systems into a theory.
In special relativity, the standard inertial coordinate systems have a special status. They not only allow us to label events with four numbers. They are "metrically significant." Their differences also allow us to determine measurable distances between points in spatial hypersurfaces; and the times elapsed along timelike worldlines. They also enable us to pick out inertial motions. They are described simply as those trajectories for which the spatial coordinates x, y and z of a point depend linearly on time. (For example, a point moving on a timelike geodesic at half the speed of light in the x direction is described by x = c/2 t, y = z = 0.)
When we move to arbitrary coordinate systems, we lose this metrical significance. To preserve this part of the physical content of the theory, we need to recapture this metrical information. That is done by making the mathematical structure associated with this metrical information explicit.
Here is a simple example of how these structures are made explicit. The example is one-dimensional. Consider times into the future. We can measure these times in the usual way by using well-constructed clocks. We can then talk of what happens a year from now, ten years from now, a hundred years from now, and so on. In the near future, a change of just one year is significant. If we are considering time millions of years into the future, then a mere one year difference is insignificant. So we might like to use a time coordinate that compresses times in the more distant future. A simple way to do this is to use the base-10 logarithm of the ordinary time.
That is, if T = time read by clocks then logarithmic time t is
t = log T
It is easy to go back and forth between the two time coordinates of some event. t = log T takes us from clock time to logarithmic time. T = 10t takes us back from logarithmic to clock time.
| Logarithmic time t | Clock time T |
| 0 | 1 |
| 1 | 10 |
| 2 | 100 |
| 3 | 1,000 |
| 4 | 10,000 |
| 5 | 100,000 |
| 6 | 1,000,000 |
| ... | ... |
| Differences of clock time T tell us how
much time has elapsed as measured by a physical clock.
Differences of logarithmic time t do not tell us this, or at least
they do not do it directly. At each epoch of time, there will be a
conversion factor to be applied to small differences of logarithmic
time t to recover the amount of clock time T elapsed that they
represent. For small differences of clock time ΔT and logarithmic time Δt, the conversion factor is: |
For those who want the general case, it requires
only a little calculus. We have some arbitrary new time coordinate t(T) as a function of the clock time coordinate T. Small increments ΔT and Δt in the two are related by ΔT =(dT/dt) Δt For the special case of t = log10T or equivalently T = 10t, we have that dT/dt = loge10 10t = loge10 T = 2.3025 T For more, see the Technical Appendix. |
ΔT = 2.3025 T Δt
The quantity 2.3025 T functions as a "temporal
metric." That is, using it we can take small differences of
logarithmic time Δt and convert them into times elapsed as read by clocks.
For example, we might ask
How much clock time elapses when we go from logarithmic time t = 2.000 to
t = 2.001?
The difference is Δt = 0.001. Applying the above formula,we find that the
clock time elapsed is
ΔT = 2.3025 T Δt = 2.3025 x 100 x 0.001 = 0.23
This fits with a direct translation of logarithmic time in clock time. t =
2 corresponds to T = 100. t = 2.001 corresponds to T = 100.23.
This temporal metric is just a particular instance of a temporal metric. For any new time coordinate t that we introduce, we can find a corresponding temporal metric. (The formula is given in the sidebar above. It is (dT/dt).
| The last section shows us how to take a one-dimensional theory of time and render it generally covariant. The same technique works for a four-dimensional spacetime theory. In special relativity, the coordinates T, X, Y and Z adapted to an inertial frame of reference have metrical significance. If we now replace them by some arbitrary set of four coordinates, x0, x1, x2, x3, we lose this metrical significance. We must recapture the physical content carried by the original coordinate system T, X, Y and Z. | I have followed the convention in general
relativity of putting the index label
"upstairs" as a superscript. The four coordinates are xindex
label, where index label = 0, 1, 2, 3. This notation should
not be confused with "x raised to power of ..." The reason that this
system is used is that it allows for a compact notation for
summations over indices. Indices upstairs are summed with matching
indices downstairs in a convention introduced by Einstein that is
known as the "Einstein summation convention." (What else could we
call it?) For more, see Technical Appendix. |
As with the one-dimensional time theory, we do this by introducing correction factors that allow us to recover the lost metrical facts. However a single number no longer suffices. We need a whole table of 16 numbers to do the job. For formal reasons these 16 numbers are represented as a two index table: gfirst index, second index, where the indices run from 0 to 3. Following Einstein, Geek letters mu "μ" and nu "ν" are common choices as labels for the first and second indices.
| gμν
= |
|
This table is the spacetime metric. We will write is as gμν or just g, as needed. If we have events whose coordinates differ only by a small increment, we can use this table to determine the proper time difference between the events (if they are timelike related) or the proper distance between them (if they are spacelike related). These space and time differences combine to give us the notion of "interval" described in an earlier chapter. This information is sufficient to determine which are the inertial motions. For, as we saw in an earlier chapter, inertial motions are those timelike curves that have maximum proper time elapsed.
This table of values also fixes the light cone structure (described in an earlier chapter) of the spacetime. For there is a zero interval between events that are lightlike separated. So when this table specifies which events are separated by zero interval, it automatically specifies the light cone structure.
To specify all the metrical information in a spacetime, we
need an assignment of one of these table to each
event in spacetime, that is, to each quadruple of spacetime
coordinates. In special cases, the same table is assigned to each event.
In general, a different table is assigned to each event.
If we know the table in one coordinate system at some event, we can determine what it is in another by a standard set of rules.The particular set of rules used for this transformation determine the mathematical character of this spacetime metric. The details need not detain us there, other than to mention the name. This table of quantities transform "tensorially" so that this quantity is known as the "metric tensor."
For more details, if you want them, see Technical Appendix.
If we start with the metric tensor as introduced above, it is a mechanical matter to fill in the remaining parts of the theory so that it is, in its entirety, generally covariant. Such a theory, however, does not automatically implement a generalized principle of relativity. The quickest way to see this is to note that everything described above pertains to the Minkowski spacetime of special relativity. The same methods are used in the general theory of relativity to secure general covariance. However they also work for special relativity. Special relativity has a relativity of inertial motion only. Rewriting the theory in a generally covariance form does not change this fact.
We can use the metric tensor to make more precise how a symmetry transformation works. What is it for the spacetime to "look the same" when we move from one coordinate system to another? It is so if we recover exactly the same table of numbers in the metric tensor gμν.
To see how this works, take the standard coordinate systems adapted to an inertial frame of reference in special relativity. In all such coordinate systems, the metric tensor adopts the especially simple form at every event:
| -1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
Here, the units for measuring
space and time are chosen so that the speed of light comes out to unity;
that is, c=1.
When we use the Lorentz transformation to transform to the standard coordinate of some other inertial frame of reference, we recover exactly the same table for values of the metric tensor. In this sense, all the metrical relations of spacetime are the same, when judged from any inertial coordinate system. The Lorentz transformation is a symmetry of a Minkowski spacetime.
Now consider the transformation from an inertial frame of reference to a uniformly accelerating frame of reference, as used in the principle of equivalence. In a coordinate system adapted to the accelerating frame of reference with acceleration a, we recover a table of values for the metric tensor:
| -a2x2 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 |
The presence of the x coordinate in the first cell of the table means that we assign a different table to events according to value of the event's x coordinate.
As before, c = 1. The acceleration
a is in the X-direction of the standard coordinate system adapted to the
inertial frame of reference. The accelerating coordinate system has
coordinates t, x, y, z, where the x, y and z axes are parallel to the X, Y
and Z axes of the inertial coordinate system. This transformation is given
in its simplest form by Einstein in a much later paper: A. Einstein and N.
Rosen, "The Particle Problem in the General Theory of Relativity," Physical
Review, 48 (1935), pp. 73 - 77, on p. 74.
For details of the computation, see the Technical
Appendix.
The presence of the non-constant g00 = -a2x2 entails that the transformation is not a symmetry. For the corresponding term in the metric in the inertial coordinate system is just a constant, -1. This non-constant term in the transformed metric is responsible for the accelerating motions of free points as judged from the accelerating frame of reference.
Einstein was wrong to claim that his general theory of relativity extended the principle of relativity to acceleration. That was clear at the outset with the completion of the theory, at least to some. It was easy, however, not to pay much attention to this lacuna. For Einstein's theory was clearly an extraordinary theory of this type. One could simply turn directly to the application of the theory. Or one could repeat some version of Einstein's claims, without reflecting too much on them, and then move on to the applications of theory.
Some did seek to correct Einstein. Most detailed of these efforts was a 1917 paper by Erich Kretschmann. It showed in lengthy, detailed analyses that general covariance was not sufficient to extend the principle of relativity to acceleration, but that what we now call an expansion of the symmetry group of a theory is what would be needed.
The paper was well-argued and needed a response. Einstein gave it in a paper of 1918. In it, Einstein now conceded that he had not made distinctions he should have made. He now gave a more complicated account of what he saw as the founding principles of his theory. They resided in three principles.
"(a)
Principle of relativity. The laws of nature are only assertions of
timespace coincidences; therefore they find their unique, natural
expression in generally covariant equations.
(b) Principle of equivalence. Inertia and weight are identical in
essence. From this and from the results of the special theory of
relativity, it follows necessarily that the symmetric ‘fundamental tensor’
(gμν) determines the metric properties of space, the inertial
relations of bodies in it, as well as gravitational effects. We will call
the condition of space, described by the fundamental tensor, the
‘G-field.’
(c) Mach’s principle. The G-field is determined without
residue by the masses of bodies. Since mass and energy are
equivalent according to the results of the special theory of relativity
and since energy is described formally by the symmetric energy tensor (Tμν),
this means that the G-field is conditioned and determined by the energy
tensor."
A. Einstein, "Prinzipielles zur allgemeinen Relativitaetstheorie," Annalen der Physik, 55 (1918), pp. 240-44.
This response codified a fragmentation of Einstein's account of the foundations of his general theory of relativity. If it was not already clear, it was now clear that Einstein's theory was not simply founded on a single principle, a generalized principle of relativity. Rather Einstein had drawn upon a collection of ideas from the start. During the years of his construction of the theory, whether all the parts fitted perfectly was a matter of lesser concern. What mattered was that this collection of ideas was leading Einstein towards an extraordinary new theory. Once the theory was completed, Einstein's standard narrative for the the foundations of the theory was to recount the ideas that guided him.
Taking Einstein's three principles in turn:
(a) Principle of Relativity. What is striking in this formulation is that the principle no longer directly asserts a relativity of all motion. Its import has migrated in a way to be explored below.
(b) Principle of Equivalence. Einstein's emphasis is no longer on the idea of treating accelerated motion as rest. Rather the immediate import of the principle is that the structures in spacetime that account for inertial motions are the same that will cover gravity.
(c) Mach's Principle. This is the latest
development of ideas we have already seen
earlier as the "relativity of inertia." Einstein had held out hope
that this general theory of relativity would implement some version of the
relativity of inertia or Mach's Principle. However these hopes faded and
eventually Einstein abandoned the principle entirely.
In place of Mach's Principle, Einstein retracted to a concern that Mach's Principle was supposed to remedy. There is, he asserted, a causal defect in classical physics and special relativity. Here is how Einstein described the problem in his 1921 Meaning of Relativity (Lecture III):
"All of the previous considerations have been based upon the assumption that all inertial systems are equivalent for the description of physical phenomena, but that they are preferred, for the formulation of the laws of nature, to spaces of reference in a different state of motion. We can think of no cause for this preference for definite states of motion to all others, according to our previous considerations, either in the perceptible bodies or in the concept of motion; on the contrary, it must be regarded as an independent property of the space-time continuum. The principle of inertia, in particular, seems to compel us to ascribe physically objective properties to the space-time continuum. Just as it was necessary from the Newtonian standpoint to make both the statements, tempus est absolutum, spatium est absolutum, so from the standpoint of the special theory of relativity we must say, continuum spatii et temporis est absolutum. In this latter statement absolutum means not only “physically real,” but also “independent in its physical properties, having a physical effect, but not itself influenced by physical conditions.” "
Einstein's retreat to the dignity of classical Latin is, as far as I can see, a bluff. For whether space and time conform with classical physics or special relativity is an empirical matter. There is no deeper law of nature with a Latin pedigree that prohibits things that act without being acted upon. The philosopher Moritz Schlick objected already in 1920 to Einstein's causal ruminations. He wrote:
". . . we can . . . consider the expression ‘absolute space’ to be a paraphrase of the mere fact that these [centrifugal] forces exist. They would then simply be immediate data; and the question why they arise in certain bodies and are wanting in others would be on the same level with the question why a body is present at one place in the world and not at another. ...I believe Newton’s dynamics is quite in order as regards the principle of causality."
Moritz Schlick, Space and Time in Conremporary Physics. Trans H L Brose (New York Oxford University Press, 1920), p. 40.
Nonetheless, the idea of a causal defect in spacetime theories prior to general relativity has persisted in a later tradition that decries such theories as harboring objectionable "absolute objects."
A fuller recounting of the fragmentation of Einstein's foundational account goes beyond what is possible here, beyond the few remarks above. For a more extensive account, including details of Kretschmann's 1917 paper and Einstein's 1918 response, see my "General Covariance and the Foundations of General Relativity: Eight Decades of Dispute," Reports on Progress in Physics, 56 (1993), pp.791-858.
We have seen in an earlier chapter that Einstein made a now famous distinction between constructive and principle theories. The distinction proved decisive in the last weeks of Einstein's many-year investigation into electrodynamics that led to the special theory of relativity. At the end of these investigations, he decided to formulate the theory as the logical consequences of just two principles. That decision enabled Einstein to suppress many distracting details in electrodynamics and show that his theory was really just a theory of space and time.
This distinction is now highly regarded. A move to a principled foundation for a theory is a prized advance. There is a danger, however. What if the theory does not admit a formulation in terms of the simple principles of the type Einstein favored? Efforts to persist in finding them will immerse the theory in a swamp of foundational confusions.
This, I believe, was the fate of general relativity in Einstein's hands. For Einstein's mutating collection of principles provide a poor foundation. Just about any theory of space and time can be given generally covariant formulation if one is persistent and ingenious enough. It follows that very little can be deduced from a principle of general covariance.
In its place, the foundations of the general theory of relativity can be given merely by reciting familiar facts in general relativity. A Minkowski spacetime is a workable theory of space and time in small regions of spacetime, remote from great masses. To cover the full range of gravitational processes, one merely posits that these further processes manifest in the curvature of spacetime. What remains are the details of matching the extent of the curvature to the magnitudes of stress-energy-momentum in spacetime. This is how the theory was introduced in an earlier chapter.
Einstein's goal, in seeking an extension of the principle of relativity to acceleration, was to deprive inertial frames of reference the preferred status they enjoyed in special relativity. At the outset of these efforts, he used spacetime coordinate systems as surrogates for frames of reference and their states of motion. As Einstein's investigations developed, his conceptions migrated and mutated. By the time of the completion of his general theory of relativity in 1916, his target was no longer the coordinate systems that represent inertial motions. Rather it was coordinate systems in their own right.
An adequate theory, Einstein now urged, should afford spacetime coordinate systems no independent existence. This, he now saw, was the real import of general covariance. For, as we have seen above, the procedure for casting a theory into a generally covariant form requires extracting physical content tacitly held in the preferred coordinate systems and recapturing that content as explicit structures in the spacetime.
There seems to me to be no problem in using preferred coordinate systems to carry the physical content of a theory. So I find it hard to agree with Einstein's insistence that we have to deprive coordinate systems of this physical content. How is the analytic geometry of Euclidean space defective if we restrict ourselves to Cartesian coordinate systems?
However it became clear that the general covariance of general relativity has deprived spacetime coordinate systems of their independent existence. The full extent of this loss was not immediately recognized by Einstein. It was a hard-won insight that took him through a noteworthy episode in the history of relativity: Einstein's "hole argument" against general covariance and its subsequent repudiation in the "point-coincidence" argument.
This, we shall see, is what Einstein reported in the first of his three principles of 1918, the (reformulated) principle of relativity.
Einstein's work on his hole argument and its repudiation
is the subject of the next
chapter, whose content follows directly from that of this chapter.
Copyright John D. Norton. November 12, 2019.