|
John D. Norton
Induction and Confirmation
material theory and
later papers
|
|
home >> research
>> induction and confirmation (material) |
|
Here is a systematic survey of the many accounts of induction and
confirmation in the literature with a special concern for the basic
principles that ground inductive inference. I believe it is possible
to see that all extant accounts depend on one or more of three basic
principles. |
"A Little Survey of Induction," Prepared for
Conference on Scientific Evidence, Center for History and Philosophy
of Science, Johns Hopkins University, April 11-13, 2003; to appear
in P. Achinstein, ed., Scientific Evidence: Philosophical and
Historical Perspectives (provisional title).Preprint
on philsci-archive.pitt.edu |
|
I do not believe, however, that any of these principles works
universally and can ever be applied without some sort of adjustment
to the case at hand. This has led to a proposal about the nature of
inductive inference. I urge that we have been misled by the model of
deductive inference into seeking a general theory in which inductive
inferences are ultimately licensed by their conformity to universal
schemas. Instead, in a "material theory of induction," I urge that
inductive inference is licensed by facts that prevail in particular
domains only, so that "all induction is local." |
"A Material Theory of Induction" Philosophy of
Science 70(October 2003), pp. 647-70. Download.
|
|
In other studies I defend the power of induction. I believe that
the popular underdetermination thesis is essential groundless
speculation based on a superficial treatment of inductive inference;
and that the much feared threat of "grue" to induction is greatly
overrated. |
"Must Evidence Underdetermine Theory?" in The
Challenge of the Social and the Pressure of Practice: Science and
Values Revisited, M. Carrier, D. Howard and J. Kourany, eds.,
Pittsburgh: University of Pittsburgh Press, 2008, pp. 17-44. Download.
"The Formal Equivalence of Grue and Green and How It Undoes the New
Riddle of Induction." Synthese, (2006) 150: 185-207. Download.
|
 |
The probability calculus is not the universal logic of induction;
there is no such thing. An axiom system disassembles the probability
calculus into distinct notions about induction, which it is urged,
may be invoked independently to tailor a logic of induction to the
problem at hand. The probability calculus fails as the inductive
logic of certain indeterministic systems. |
"Probability Disassembled," British Journal for
the Philosophy of Science, 58 (2007), pp. 141-171. Download.
|
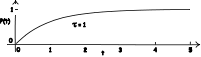
|
A simple indeterministic system is displayed and it is urged that
we cannot responsibly infer inductively over it if we presume that
the probability calculus is the appropriate logic of induction. The
example illustrates the general thesis of a material theory of
induction, that the logic appropriate to a particular domain is
determined by the facts that prevail there. |
"Induction without Probabilities." Download.
See also "Induction without
Probabilities" in Goodies.
|
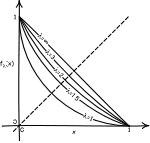
|
The epistemic state of complete ignorance cannot be a probability
distribution. The instruments that characterize it are innocuous
platitudes of evidence: the principle of indifference and certain
invariance conditions. However the literature has misdiagnosed these
instruments as defective since these instruments rule out the
representation of complete ignorance by probability distributions. |
"Ignorance and Indifference." Download.
|
 |
This paper illustrates how the material theory of induction can be
used to assess evidence claims made historically in science. Two
cases are considered: Einstein's 1905 thermodynamic argument for
light quanta and his 1915 recovery of the anomalous perihelion
motion of Mercury. |
"History of Science and the Material Theory of
Induction: Einstein's Quanta, Mercury's Perihelion." Download. |
 |
Forming the dual is a familiar operation in logic and mathematics.
Truth is the dual of falsity; and (A or B) is the dual of (A and B).
Here I develop the corresponding notion for additive measures, such
as probability measures. The resulting dual additive measures are
degrees of disbelief and turn out to obey their own peculiar
calculus. An ignorance state is conveniently characterized as one
that is self-dual. |
"Disbelief as the Dual of Belief" Download. |
 |
While Bayesian analysis has enjoyed notable success with many
particular problems of inductive inference, it is not the one true
and universal logic of induction. I review why the Bayesian approach
fails to provide this universal logic of induction. Some of the
reasons arise at the global level through the existence of competing
systems of inductive logic. Others emerge through an examination of
the individual assumptions that, when combined, form the Bayesian
system: that there is a real valued magnitude that expresses
evidential support, that it is additive and that its treatment of
logical conjunction is such that Bayes' theorem ensues. |
“Challenges to Bayesian Confirmation Theory,”
Prepared for Prasanta S. Bandyopadhyay and Malcolm Forster (eds.), Philosophy
of Statistics: Vol. 7 Handbook of the Philosophy of Science.
Elsevier. Download draft. |
 |
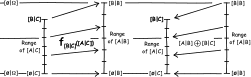
What if, like me, you don't think that the probability calculus is
the One, True Logic of Induction? Then you want to know what other
logics are possible. Here I map out a large class of inductive
logics that originate in the idea that the inductive support B
affords A, that is "[A|B]," is defined in terms of the deductive
relations among propositions. I demonstrate some very general
properties for these logics. In large algebras of propositions, for
example, inductive independence is generic in all of them. A no-go
result forces all the logics to supplement the deductive relations
among propositions with intrinsically inductive structures. |
"Deductively Definable Logics of Induction" Download.
For a less formal development, see "What
Logics of Induction are There?" in Goodies. |

|
In a material theory of induction, inductive inferences are
warranted by facts that prevail locally. This approach, it is urged,
is preferable to formal theories of induction in which the good
inductive inferences are delineated as those conforming to some
universal schema. An inductive inference problem concerning
indeterministic, non-probabilistic systems in physics is posed and
it is argued that Bayesians cannot responsibly analyze it, thereby
demonstrating that the probability calculus is not the universal
logic of induction. |
"There are No Universal Rules for Induction" Download
|
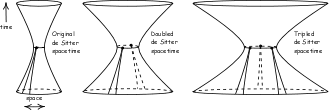 |
What should we infer from the possibility of observationally
indistinguishable spacetimes? I urge they are not a manifestation of
the dubious thesis of the evidential underdetermination of theory,
but a form of indeterminism within a theory. Moreover inductively
discriminating among the spacetime requires inductive inferences
that are "opaque" in the sense the we cannot see through them to
their warrant. |
"The Inductive Significance of Observationally
Indistinguishable Spacetimes." Download |
 |
Which are the good inductive inferences or the proper relations of
inductive support? We have sought for millennia to answer by means
of universally applicable formal rules or schema. These efforts have
failed. Background facts, not rules, ultimately determine which are
the good inductive inferences. No formal rule applies universally.
Each is confined to a restricted domain whose background facts there
authorize them.
My book, The Material Theory of Induction is now available
as a full manuscript. Contents:
Preface
Prolog
1. The Material Theory of Induction Stated and Illustrated
2. What Powers Inductive Inference?
3. Replicability of Experiment
4. Analogy
5. Epistemic Virtues and Epistemic Values: A Skeptical Critique
6. Simplicity as a Surrogate
7. Simplicity in Model Selection
8. Inference to the Best Explanation: The General Account.
9. Inference to the Best Explanation: Examples
10. Why Not Bayes
11. Circularity in the Scoring Rule Vindication of Probabilities
12. No Place to Stand: the Incompleteness of All Calculi of
inductive Inference
13. Infinite Lottery Machines
14. Uncountable Problems
15. Indeterministic Physical Systems
16. A Quantum Inductive Logic
Epilog
|
Download
complete manuscript of April 24, 2020. |

|
A special issue of Studies in History and Philosophy of
Science is on the material theory of induction and has 14
papers. Here are my responses to those papers. |
Download draft. |
|
|