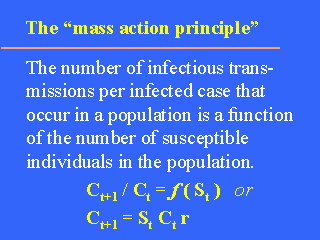|
 |
front |1 |2 |3 |4 |5 |6 |7 |8 |9 |10 |11 |12 |13 |14 |15 |16 |17 |18 |19 |20 |21 |22 |23 |24 |25 |26 |27 |28 |29 |
|
Search for most updated materials ↑
The "mass action
principle" states that this rate is a function of the number susceptible individuals
in the population, i.e.: Ct+1/Ct =
f (St), where C is the number of
infected cases, S the number of susceptibles, t a given time period, t+1 the next time
period. This can also be expressed as: Ct+1 = St Ct r, where
r is a transmission
parameter. (The latter expression explains the name of the "mass action principle",
which was given by analogy to the "law of mass action" in chemistry, according
to which the velocity of a chemical reaction is a function of the concentrations of the
initial reagents.) The "mass action principle" is actually the theoretical basis of the
phenomenon of herd immunity. It was introduced in the 1900’s and helped understand
the dynamics of epidemics of diseases like measles: as the infection spreads during an
epidemic, the number of infected cases in each successive time period initially increases
while the number of susceptibles in the population decreases; therefore, there will be a
point when susceptibles become sparse and the number of new cases in each successive time
period decreases; and, finally, susceptibles are so scarce that there is no more than one
new case for each case in the previous time period, and the epidemic fades out although a
number of susceptibles have not been infected.
|