NCSA Nanotechnology Initiative

Testing transition state searching algorithms for use with plane-wave DFT codes

Information on activation barriers is of central importance for estimating rates, providing an understanding of mechanisms and evaluating possible rate-enhancing modifications. Transition state optimization methods employed in non-periodic ab initio codes (such as Gaussian 98, Jaguar, and Spartan generally use analytic first derivatives together with analytical or good numerical estimates of the Hessian. Most theoretical work on periodic systems (surfaces and bulk) is currently carried out using plane-wave methods for which accurate evaluation of the Hessian is difficult due to the use of grids.

Two promising non-Hessian based transition state optimization algorithms are the Ridge algorithm^1,2 (from Carter's group at UCLA) and the Nudged Elastic Band (NEB) algorithm ^3,4 (from Jónsson's group at U. of Washington).

We are testing these algorithms as implemented in plane wave codes for locating transition states for various surface rearrangement processes. Below we summarize the main features of the NEB algorithm, which has been used in most of our studies to date.

The NEB algorithm, which is an improvement of the previously used Elastic Band algorithm, only requires evaluation of the potential energy and its first derivatives. It converges to the minimum energy path (MEP) in a well-defined limit. The transition state corresponds to the highest energy point along the MEP. The NEB algorithm is highly parallelizable since it involves multiple constrained minimizations that can be carried out simultaneously and that do not require much interprocessor communication. The computational effort grows slowly with system size.

Outline of the Elastic Band Method

• Let R₀ and R_P denote the coordinates of the reactant and product, respectively. (These are 3N component vectors where N is the number of atoms.
• A set of intermediate points or "images" of the system is generated by interpolation between the reactant and product in coordination space. These images define a discrete representation of a path connecting reactant and product.
• A constrained minimization of these images is done so that they descend in energy to the MEP without collapsing to either the reactant or the product.
• This is accomplished by constructing an object function F that includes a spring force between neighboring images.
  
  

Shortcomings

• The spring force causes "corner cutting" and thus the algorithm does not converge to the exact MEP.
• The density of the images is lowest near the highest points of the path and so resolution is worst in the region of the saddle point.

Outline of the Nudged Elastic Band Method

The NEB algorithm addresses the shortcomings of the simple elastic band methods by setting the spring force in directions perpendicular to the the path equal to zero (this solves the "corner cutting" problem) and by setting the true forces along the path to zero (this prevents the images from sliding towards the endpoints and improves the density of images near the transition state).

The unit vector is tangent to the path at the point t. The unit vectors are perpendicular to the path at t. The forces acting on the images are redefined so as to:

• Zero out the perpendicular component of the net spring force.
• Zero out the parallel component of the true interaction potential.

What the Jordan Group is Doing With NEB

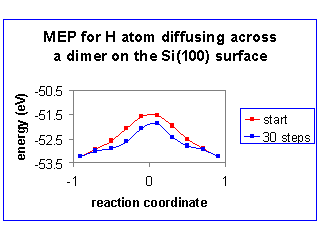
Initial tests of NEB interfaced with the VASP plane-wave DFT code are encouraging. The figure below depicts the results for a NEB optimization of the reaction path for an H atom hopping between the Si atoms of an Si-Si dimer on the Si(100)-2x1 surface. The calculated barrier - 1.50eV - is identical to that found by minimization with symmetry imposed.

We have recently employed the NEB algorithm to map out the MEP for 3x1 ---> 2x1 rearrangements on the Si(100) surface. The reaction pathway for the rearrangements is very complex.

This research has been accepted for publication in Surface Science.⁵

In the future, we plan to:

• Develop a web-based implementation of NEB in conjunction with various model potentials.
• Incorporate NEB into a MM/QM model for electrons interacting with water clusters.