
John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
This page at http://www.pitt.edu/~jdnorton/Goodies

For more images and much more commentary on the Zurich Notebook, look here.
In the half century and more of Einstein's work in science, one discovery stands above all as his greatest achievement. It is his general theory of relativity. In it, Einstein found a new way to think of the gravity that pulls apples from their trees and keeps the moon in orbit around our earth. There are no forces pulling on them, he saw. They are merely responding to a curvature in the geometrical fabric of space and time.
This discovery of this theory is somehow more than mere science. It is not the fitting of a formula to a set of data or the succumbing to the weight of unanswerable evidence. General relativity was an achievement of creative imagination. Through it, Einstein found the boundary of science and art. There he wrote equations linking space, time, matter and gravity every bit as beautiful as Shakespeare's sonnets, but written in the universal language of mathematics. The evidence that favors general relativity is no where near as strong or thorough as that which speaks for quantum theory. Yet we favor general relativity simply because no conception this beautiful should be wrong. And it survives because no theorist in the many decades since 1915 has been imaginative enough to find a theory that does better than general relativity. Every time a new test is devised Einstein's theory wins.
| Einstein's search for general relativity spanned
eight years, 1907-1915. Some periods were quiet and some were more
intense. The moments when the great transition
occurred, came sometime between the late summer of 1912, when
Einstein moved from Prague to Zurich, and early 1913. If we could
choose one time at which to look over Einstein's shoulder and watch him
work on general relativity, it would be this time. And that is just what we can do. For, found among his papers when Einstein died in 1955 was a small, brown notebook containing his private calculations from just this time. This is the Zurich notebook. |
Prior to his move to Zurich in August 1912, Einstein
was grappling with the puzzle of accommodating gravitation into his
1905 special theory of relativity. His reflections had borne some
fruit, but they were rudimentary, in comparison to what was to come,
and still in the simple mathematics of his work of 1905. Then he saw it, the connection between gravity and non-Euclidean geometry. On could introduce the most general gravitational fields in the spacetime of special relativity merely by curving its geometry. In a few short months, he sketched the structure of the theory based on this idea and began to home in on its central equations that would describe how source matter would affect the geometry of spacetime. Everyone who knows general relativity is familiar with those equations. They set two quantities equal. One, the "stress-energy tensor," is simply a compilation of the properties of matter at each point in spacetime. It is a big table whose entries include energy density, momentum fluxes and stresses. The other is a purely geometric quantity, built out of quantities that measure how spacetime curves in the many dimensions that comprise it. That quantity is now known as the Einstein tensor and it is formed from another quantity discovered by the 19th century geometer and mathematician, Riemann. It is called, as you'd guess, the Riemann tensor. Einstein circled around these equations. But then he abandoned them and by early 1913, settled on a set of equations with no clear geometric meaning. That this should happen is, to modern relativists, unimaginable. Yet it did. Einstein suffered terribly for nearly three years as he tried to resolve the resulting mess before presenting the famous Einstein equations that complete his theory. |
Let us start at the beginning. The notebook has two front covers. Einstein wrote in it in both directions. There is the front cover shown above and first here. It has Helen Dukas, Einstein's secretary's, typed description of the notebook as "Notes for Lectures on Relativity..." If we flip the notebook over, we find a second cover with the word "Relativity" in Einstein's hand.


Inside the "Relativity" cover are a few rough sketches shown below. They are wonderfully human and wonderfully revealing. I wonder if you know what they are?
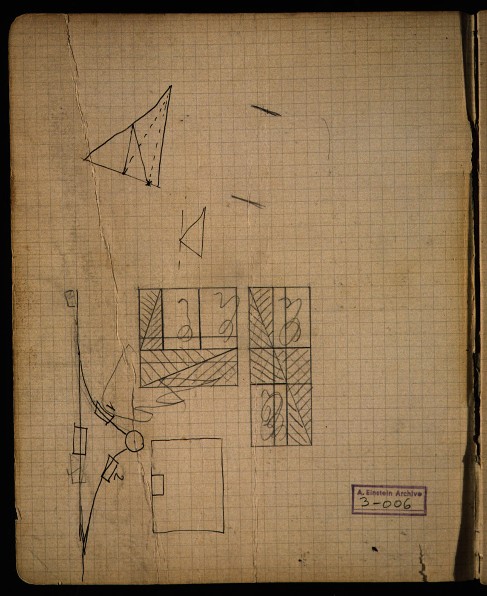
| Do you know? They are recreational
puzzles in mathematics. One appears to be a well-known puzzle relating the shunting of railroad cars on tracks. The lines are the tracks and the cars are the small rectangles. |
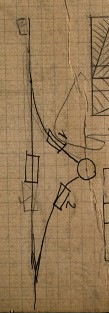 |
What of the square and rectangles with the cross-hatching?
They are an old puzzle in which we prove that a square of size 8x8 = 64 units
can be cut into pieces and reassembled as a rectangle of size 13x5=65 units.
That is, we are proving
64 = 65
| Here's how it works. First start with the square. Cut it into the rectangles shown and cut some of those diagonally as shown. | 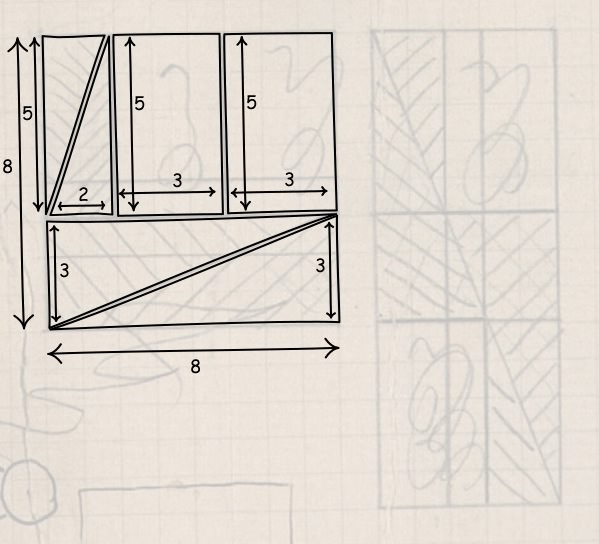 |
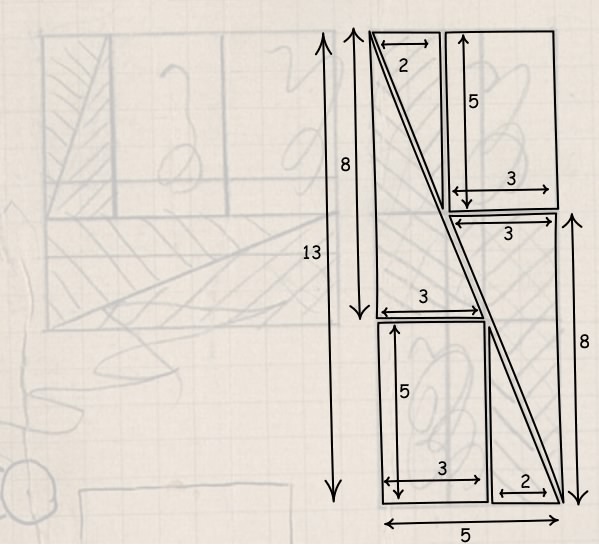
|
Now just take each of those pieces and lay them over
the 13x5 rectangle to cover the rectangle completely. The 64 units of area of the square now covers the 65 units of area of the rectangle 64=65 OK. It really doesn't work and of course Einstein knew it. But do you know where the fallacy lies? Here's the solution in case you don't want to spend a moment pondering. And now here's the bigger puzzle: why was Einstein playing around with this puzzle? Who did he want to amuse? Some children? Perhaps his own? |
This inside cover was recreational. The page that faced it, however, contained serious physics. There we find Einstein recounting the elements of the four-dimensional approach to relativity and electrodynamics of Minkowski, starting with the four spacetime coordinates (x, y, z, ict) = (x1, x2, x3, x4) and proceeding through scalars, four-vectors and six-vectors and the operations allowed with them.

The development continues for 13 pages recounting notions in electrodynamics and thermal physics. Then it takes a dramatic turn.
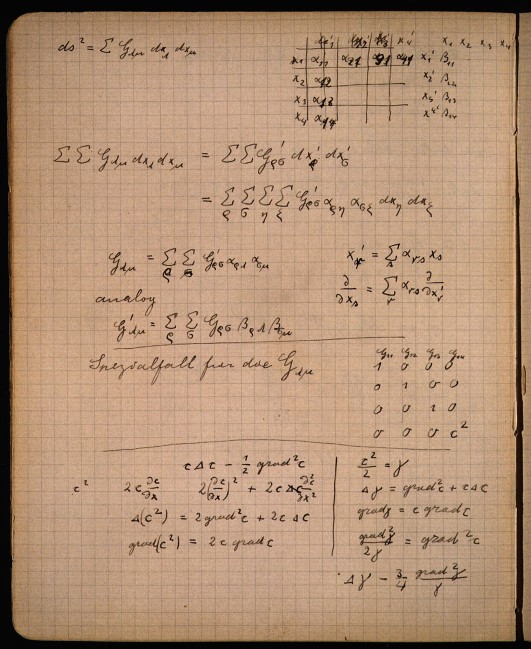
Suddenly, without any warning of the transition, we find the
basic notion of general relativity, the "line element" written at the top of
the page.
![]()
The coefficients Gμν enable us to compute the spatio-temporal
interval ds between events separated by infinitesimal coordinate differences
dxμ. If these coefficients assign spatio-temporal intervals that
do not conform to a flat geometry, then we have captured the full range of
gravitational effects in the manner of Einstein's general theory.
This is quite possibly the first time Einstein has written down this expression. The coefficients Gμν of what we now know as the "metric tensor" are written with an upper case G. Einstein shifted within a few pages to the lower case g, which remained his standard notation from then on.
The big project is to find how this quantity gμν, the metric tensor, is generated by source masses. These are the "gravitational field equations." That is this theory's analog of Newton's inverse square law of gravity. The lower half of the page is clearly making rudimentary efforts in that direction. There Einstein chooses a "Spezialfall" -- a special case -- in which the coefficients of the metric tensor revert to the values of special relativity, excepting G44 = c2. Einstein then tries to apply the gravitational field equation from his 1912 theory of static gravitational fields.
Einstein's analysis continues at this simple level on the facing page.There he asks beginner's questions. He looks at the coordinate divergence of the metric tensor and asks "Ist dies invariant?"-- "Is this invariant?" As the computation that follows immediately shows, it is not.

How these quantities transform under change of coordinates is clearly a major focus of his analysis. What is very noticeable is that Einstein has not yet used any of the techniques of the Ricci and Levi-Civita absolute differential calculus, now called "tensor calculus." Instead he uses older methods due to Beltrami to see what invariant quantities can be formed from a scalar φ.

The analysis continues for three more pages and then we find one of the most fascinating pages.

Here Einstein finds several of the key notions of his new theory in an unexpected arena, classical physics. What Einstein does is to rederive a standard result in classical physics. If a mass is free to move inertially except that it is constrained to move within a curved surface, what is the curve traced by the mass in surface? It proves to be a geodesic of the surface, a curve of shortest distance.
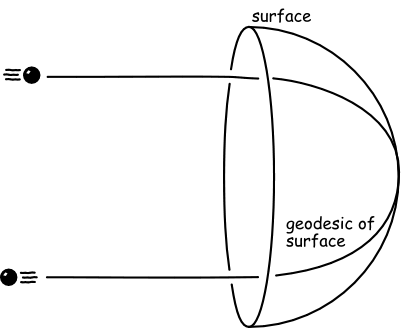
The result is eerily close to the central idea of Einstein's general theory of relativity. The table shows how close it comes.
| Classical physics | General relativity |
| A mass moves freely in space, except that it is constrained to a two-dimensional surface in the three-dimensional space. | A mass moves freely in spacetime. That is, it is in free fall, so that gravity acts on it through the curvature of spacetime. |
| Its spatial trajectory is a geodesic of the two-dimensional surface. That is, it traces of curve of shortest length in the surface. | Its spacetime trajectory is a geodesic of the spacetime. That is, it traces a curve of extremal spacetime interval in spacetime. |
Here's how the calculation starts out. The surface is defined by a scalar field f in space. Constant values of f, such as f=0, pick out the surface. The equation of motion of the mass moving in the surface is just that its acceleration vector (d2x/dt2, d2y/dt2, d2z/dt2) is proportional to the reaction force from the surface, which is orthogonal to the surface and proportional to the gradient of f, (∂f/∂x, ∂f/∂y, ∂f/∂z). All this is summarized in:
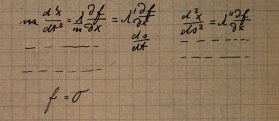
Immediately underneath is a straightforward derivation within the calculus of variations. If a mass point in the surface obeys these equations of motion, then the spatial length of the path traced on the surface, ∫ds, is extremal, in that it satisfies the condition δ∫ds=0. Here is a reconstruction of all the steps of this calculation.
That this is the import of this computation is easy to see once someone shows you. Until they do, it is virtually impossible to see. Tilman Sauer was first to see what Einstein was up to on this page.
These computations proceed until we reach a page on which calculations from each side of the notebook meet.

So we flip the notebook over and start at the other side. We proceed through a series of pages of computation in the statistical-thermal physics of heat radiation. The first page, for example, is this:

At the top of the page, Einstein has written the Planck
formula for the energy density of thermal radiation.

He then takes its derivative with respect to temperature T in order to arrive
at his famous fluctuation formula from 1909.
After nine pages like this, Einstein starts a new heading, "Gravitation," and we are thrown into the thick of general relativity.

On this page Einstein sets up the equations for conservation
of energy and momentum for continuous matter in general relativity. He starts
with the equation of motion for a point mass--the geodesic equation--but now
written in the form of an Euler-Lagrange equation:
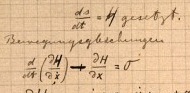
He then applies this to a cloud of non-interacting dust particles in free fall
to arrive at what we now recognize to be the condition of the vanishing of the
covariant divergence of the stress energy tensor Tμν.
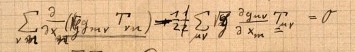
However there is good evidence that Einstein's knowledge of tensor calculus is
still limited. He does not know or is not sure that the operator acting on
Tμν in this equation is a generally covariant operator. To
check the operator, he replaces Tμν by the tensor
gμν and sees whether the result is zero or a four vector ("0
oder Vierervektor"), as it should be if the operator is generally covariant. It
proves to be zero and Einstein is satisfied. He writes "Stimmt"--"Correct".
If Einstein was feeling a little smug, he had every right to it. For he had just used physical argumentation to generate one of the basic covariant operators of the tensor calculus.
The pages continue with increasingly elaborate attempts to form invariant quantities from the metric tensor, presumably in order to find a generally covariant set of gravitational field equations. One approach repeatedly explored is to investigate the properties of the determinant G of the metric tensor, as he does here:

In it he identifies an "hypothesized gravitation tensor" -- "vermuticher Gravitationstensor" -- perhaps a candidate for the gravitation tensor in the field equations; or, since it is just quadratic in first derivatives of the metric tensor, a candidate for the stress energy tensor of the gravitational field, which also may appear in such equations.
What is noticeable for its absence are the techniques of Ricci and Levi-Civita for producing invariant quantities from the derivatives of the metric tensor. Most significantly, there is no sign of the fourth rank Riemann curvature tensor from which we now know the gravitational field equations are readily constructed.
That lacuna is filled after more pages when Einstein writes at the head of the page the formula for the Riemann tensor, using the old "four-index symbol" notation, (iκ,lm).

The often-told story is that Einstein only learned of the methods of Ricci and Levi-Civita through his school friend, the mathematician Marcel Grossmann. It is Grossmann who went to the library in search of methods that could accommodate arbitrary coordinate systems. There he found Ricci and Levi-Civita's article of 1901 with the Riemann tensor and reported it to Einstein.
In accord with that often-told story, we have notation next
to the Riemann tensor that suggests that Grossmann conveyed the formula to
Einstein.
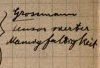
"Grossmann tensor fourth rank"
Einstein proceeded in essentially the modern way. He
contracted the fourth rank Riemann tensor to produce the second rank Ricci
tensor. If it is to serve as a gravitation tensor, it must reduce in the weak
field to a Newtonian form. This requires three of its four second order
derivative terms to vanish. Einstein noted this condition for the weak field
form of these terms
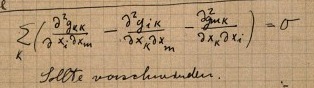
"Sollte verschwinden" -- "should vanish"
Figuring out how to eliminate these three terms in the weak field limit will become a major focus and major stumbling block for Einstein in the pages to follow.
Now knowing the Riemann curvature tensor, what follows for Einstein are pages of laborious manipulation of the large expressions it produces. One can sense Einstein's frustration building as he fails to see his way through the mounting piles of symbols. One computation is broken off with the lament "zu umstaendlich"--"too involved."

None of this seems to have been much aid in the problem of recovering the Newtonian limit and eliminating the three unwanted terms from the Ricci tensor. We now deal with this problem by stipulating a restriction of the coordinate systems to those in which we expect the Newtonian limit to appear. We must do that one way or another since we are starting with generally covariant equations and seeking to recover Newtonian equations of more restricted covariance.
A few pages later, Einstein shows that he is fully aware of the mathematical manipulations needed for the recovery of the Newtonian limit. The heading once again conveys Einstein's weariness: "Nochmalige Berechnung des Ebenentensors"--"Once again the computation of the surface tensor" and begins with the expression for the Ricci tensor.

Einstein makes quite clear what his goal is. When he is
finished, he notes, what is to remain ("bleibt stehen") is just the term in the
tensor for the Newtonian limit.
![]()
He will achieve this by stipulating that his solution must satisfy a
condition
![]()
that we now recognize as the "harmonic coordinate condition." It is a condition
used to select out a particularly useful subset of coordinates. With that
condition, Einstein completes the recovery of the equations of the Newtonian
limit successfully. He is satisfied and writes at the bottom of the page:
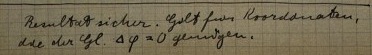
"The result is certain. Holds for coordinates that satisfy the Eqn
Δφ=0 [another way of expressing the harmonic condition]"
With this apparently satisfactory solution in hand, Einstein proceeds to investigate energy and momentum conservation for the resulting gravitational field equations in the case of weak fields. Then it all unravels. In a concluding page of these investigations, Einstein treats the special case of static fields. ("Statischer Spezialfall"--"static special case")

We can see written on this page a mistaken assumption,
repeated in his publications from this period, that is sufficient to defeat all
efforts to give the modern treatment of the Newtonian limit. Einstein assumed
that in the weak field in suitable coordinates in which the Newtonian limit
emerges, only one of the ten components of the metric tensor would vary with
the coordinates. That is g44=c2. All the other components
would remain constant.
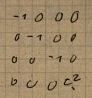
Whether this was its direct cause or not, Einstein writes at the bottom of the
page "Spezialfall wahrscheinlich unrichtig" -- "special case probably
incorrect." With that, the harmonic condition vanished from the notebook.
A lesser physicist might have become dispirited at this point. Not Einstein. He had clearly developed a considerable facility with the computations and, on the next page, displays a new solution.

Einstein writes down a reduced form of the Ricci tensor as
his new "presumed gravitation tensor."
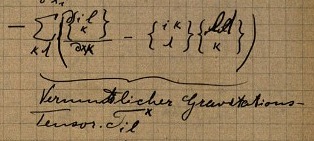
He has chosen this gravitation tensor, since he can show that it has very broad
covariance and reduces to the Newtonian limit if he assumes a new coordinate
condition:
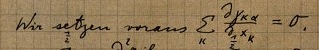
The content of this page has generated some dispute among the authors of the volume The Genesis of General Relativity. The majority view is that Einstein now inserted this equation as a new physical assumption, thereby dooming his theory to vastly restricted covariance. I hold a minority view that he regarded it as a free choice of coordinate systems. (That is why the labeled an expression prior to application of this condition as the "gravitation tensor.") However I urge that he rejected the resulting system as inadmissible because of an improper reification of coordinate systems that would come back to haunt him again shortly with his notorious "hole argument."
Whatever may have transpired, this new proposal does not survive the page. On the following page, Einstein finds yet another way to extract the Newtonian limit from the Riemann tensor.

His new idea is not to write a condition that picks out a
subset of coordinates directly. Instead it is to stipulate that we are in such
a restricted set of coordinates that a certain quantity must transform as a
tensor.
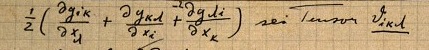
Einstein can then demonstrate that an expression with Newtonian form derived
from the Riemann tensor is a tensor under the restriction just stated.
Ingenious as it is, this third means of exploiting the Riemann tensor does not survive many pages. Soon we have complete capitulation. In his "Entwurf" paper of mid 1913, Einstein, with the assistance of Grossmann, derives and publishes gravitational field equations of unknown covariance that are not derived from the Riemann tensor. A few pages later in the notebook we find a summary of the derivation of these equations spread over two facing pages. They are displayed with a neatness and order rare among the other pages of the notebook, suggesting that they were transcribed from another place after the result was known. The underlining and symbols 0 and + are used to help in book-keeping in a complicated computation in which a terms are expanded, and rearranged by algebraic manipulation.


With these equations selected, Einstein entered a darkness in which he would wander restlessly and with increasing discomfort for over two years before returning to the successful search for generally covariant gravitational field equations in late 1915.
All that is left now is clean up. Einstein begins to sketch out a generally covariant formulation of Maxwell electrodynamics.

A complete facsimile of the notebook is available at the Einstein Archive Online at
http://alberteinstein.info/vufind1/Record/EAR000034421
or go to http://alberteinstein.info/ --> Archival Database --> Search "Zurich Notebook";
and at the ECHO Project (may load slowly)
http://nausikaa2.mpiwg-berlin.mpg.de/cgi-bin/toc/toc.x.cgi?step=thumb2;dir=Einstein_ZN;start=1;quant=10000;thumbcols=4;vf=Einstein_ZN.1213996017
A
transcription of the gravitational part of the notebook is included in
Collected Papers of Albert Einstein, Vol. 4: The Swiss Years: Writings,
1912-1914. Princeton Univ. Press. and is available online at
http://einsteinpapers.press.princeton.edu/vol4-doc See Document 10.
The authoritative and most complete discussion of the notebook, including a
facsimile, transcription, commentary and individual essays is found in Vol.1:
The Zurich Notebook and the Genesis of General Relativity and Vol.
2:Einstein’s Zurich Notebook, Commentary and Essays of J. Renn,
ed., The Genesis of General Relativity: Sources and Interpretation: Boston
Studies in the Philosophy of Science, Vol. 250. Springer 2007.
In addition to contributions to the above multivolume analysis, my "How
Einstein Found His Field Equations: 1912-1915," (download) Historical
Studies in the Physical Sciences, 14 (1984), pp. 253-315. Reprinted in D.
Howard and J. Stachel (eds.), Einstein and the History of General
Relativity: Einstein Studies Vol. I, Boston: Birkhauser, pp101-159,
provided the first analysis of the notebook.
See also "A Conjecture on Einstein, the Independent Reality of Spacetime
Coordinate Systems and the Disaster of 1913," pp. 67-102 in A. J. Kox and J.
Einsenstaedt, eds., The Universe of General Relativity. Einstein Studies
Volume 11. Boston: Birkhaeuser, 2005. Download.
June 24, 2008. June 20, 2012.
The first draft of this page was prepared on June 21, 2008, late into the
night. On the street outside our downtown loft, Pittsburgh's gay pride street
party was in full swing, with a sound stage and live music that rattled our
windows.