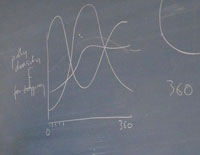::: center home >> being here >> last donut? >> butterfield |
14 November 2008 His plan was to "pour oil on troubled waters." So began Jeremy Butterfield's talk in our Annual Lecture Series. Jeremy has been a visitor this term in the Department of HPS and has popped down to the Center quite often. He is always very welcome. One of the rules we'd learned in child rearing was to catch our kids doing something well, so we could properly heap praise upon them. Jeremy has found how to carry that approach over to his academic colleagues. A meeting with Jeremy is assured to buoy flagging spirits. The debates of reduction and emergence urgently need Jeremy's talents at reconciliation. Reductionists and emergentists battle away, yet it seems incredible that each side could really believe what the other side says that they believe. Jeremy's response is to say that they are both right. We can have reduction and emergence at the same time. Jeremy limits his analysis to examples in physics. There we find lower level theories that may, or may not, tell the reductive truth about upper level theories. The lower level theories might be something like the theory of atoms and molecules; the upper level theories might be something like the thermodynamics of fluids: water and steam. What appears in all these examples is a number "N." In this case, it is the number of molecules of water in, say, a teapot. For any real teapot, N is just enormous. We might say it is so close to infinity that only the Gods can tell the difference. And therein lies the whole issue. The emergentists urge that new phenomena emerge when N goes to infinity. No finite system of water molecules, no matter how many molecules there are, can exhibit the sharp changes of properties reported in the textbooks, when water changes phase in passing to steam. Those abrupt, mathematically discontinuous transitions are "emergent." That term, Jeremy tells us, just designates "novel and robust behaviour." I have preserved the English spelling of behaviour in deference to Jeremy's perfect Oxbridge-BBC English, melded with his irrepressible whimsy, all of which lends a special charm to every sentence. So what are we to make of this? Is the thermal physics of water and steam in Jeremy's teapot something genuinely novel? Or is it reducible to the physics of many, many molecules of water? Both, is Jeremy's answer. Just how he was going to sustain this answer was in an eighteen page set of closely printed notes that he clutched as he spoke. He'd sent us a copy in advance of the talk; and, realizing that this was too much for us to read and too much for him to cover in one talk, he'd asked Peter Gildenhuys here to copy pages 1 to 4 and pages 15 to 18 as a handout. He then remarked, to Peter's great consternation, "if he thought it necessary" add in pages 5 to 6. (Judging an error of omission the greater error, we copied them.) There were four examples in this document. Jeremy really only had time to talk about two. The first, I thought, was ingenious for its simplicity and clarity. Roulette wheels and coin tosses are reliable ways of producing a random choice between red and black or between head and tail in such a way that each outcome has exactly a chance of one half. Somehow the devices are able to eradicate any of the inevitable unevennesses in the hand of the croupier. Poincare and Reichenbach had long ago explained how this was possible through the "method of arbitrary functions." Let me illustrate with a simpler example. If one throws a dart at a dartboard with a red bull's eye, the chance of hitting the red bull's eye is almost certainly not one half. How could we redesign the board so that we could make the chance one half? The solution is to repaint the board with lots of tiny red bull's eyes that together cover exactly one half the board's area. By keeping this condition and re-painting with more and more, smaller and smaller bull's eyes, we can drive the chance of hitting red as close as we like to one half, no matter how certain or uncertain the hand that throws the dart. Here is emergence. We get the exact equality of chances only in the limiting case of N, the number of red spots, actually attaining infinity. That exact equality is novel and robust; it is emergent. Yet the full analysis is given reductively in terms of the behaviour of finitely many red spots, albeit a very large number of them. By now Jeremy has abandoned the digitized image of his handout. "Time for some drama," he said. Would the screen raise, he asked. Yes--just push the "up button." What Jeremy did not know was just that morning, pushing the button would have done nothing. Our digital facilities are being upgraded with a permanent digital projector and a new screen. We arrived in the morning to find the screen sitting in a gaping hole in the ceiling with unconnected wires dangling down. Jeremy was at the blackboard and began drawing pictures of roulette wheels spinning over 360 degrees and graphing the arbitrary functions that give probabilities for where they would stop their motions. The chalky lines quickly made clear, that no matter how arbitrarily skewed the functions were, there is always a fine enough division of the wheel into red and black that would even the functions out into a serviceable randomizer. As long as the number of divisions N is big enough, we can get our function as evened out as we like. Here Jeremy was illustrating the remark he'd made earlier. We don't need to go all the way to infinity to get the emergent phenomena. It will already be manifested "on the way to infinity."
As this speech unfolded, Jeremy was gazing back, wishing he wasn't hearing all this. How can I be conciliatory, he seemed to be thinking, when you say things like that? I pressed on. Mustn't the point be that systems with large N are very close in properties to infinite N systems? So the infinite systems are useful for analysis only because they give the same results near enough, but are much, much easier to compute? "Well that isn't very interesting," Sandy called out, quite correctly. John D. Norton
|