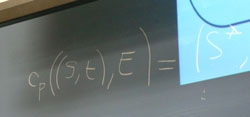Tuesday, 18 March 2008
Propensities

A new Fellow joined us in March just as we returned from our midterm break. Isabelle Drouet has just finished her doctorate in Paris at the Sorbonne and was eager to visit now, even if it meant she would come for only half a term. As it happened, we did have scarce office space for her, starting in March. So she came, swelling the ranks of the French speakers who pass through our halls. They now include Delphine Chapuis-Schmitz, a Visiting Fellow this year; a graduate student Rawad Skaff, also visiting the Dept. of HPS from Paris; and, of course, our colleague in HPS, Edouard Machery of the memorable socks. This is new. If I think back ten years, I cannot recall ever hearing French in our halls then.

Today Isabelle is speaking on her research. It concerns Popper's propensity interpretation of probability. Popper's idea was a contribution to the vexing problem of deciding just what probability statements mean. When we say that the probability of tossing a head with a coin is a half, do we really mean something about the relative frequency of heads in the outcomes of coin tosses just like this one? Don't we really mean that very probably the relative frequencies will come out somewhere around a half? For there is always the increasingly remote possibility that this fair coin will come up heads each time.

That qualification makes this definition of probability circular, for it mentions probability essentially in the definition itself. What then are we to think probabilities are? Must we become subjectivists and say that they are just our degrees of belief? Or can we find some meaning for probability in which it is an objective property of systems in the world, independent of our beliefs?

That problem was an unspoken background that Isabelle correctly presumed most people in the room knew. She began her talk by recounting the objectivist answer she favored. Popper had proposed that we forget about the troublesome sequences of tosses and just think of the one case. That one toss, or more precisely, the set of circumstances surrounding that toss, has a propensity of a half to produce a head. The propensity is an objective property of those circumstances. It confers all the expected probabilistic properties on outcomes. Through it, repeated tosses generate a sequence of heads and tails that are roughly half heads.

No solution is ever that easy. There are always problems. The leading one, she assured us, was "Humphrey's paradox." It is simple to set up. She took the example of a photon incident on a half-silvered mirror. There is a probability of a half that it is transmitted through the mirror. That is a conditional probability: the probability of transmission given (or conditioned on) the incidence of the photon.

Humphreys' paradox dealt with a quantity routinely formed in the probability calculus, the inverse probability. What is the probability of incidence given transmission? If probabilities are propensities, the answer is clear, Humphreys assures us. Transmission comes after incidence. So a later event of transmission cannot causally affect whether a photon is incident on the mirror earlier. That is not how causes work. Therefore, if probabilities are causal propensities, conditioning on transmission cannot change the probability of incidence at all. Incidence is independent of transmission.

Innocent as it sounds, that is already a fatal problem. There are different ways of seeing why. The one I like is quick and informal. It merely notes that independence in a probabilistic analysis is a symmetric relation. If incidence is independent of transmission, then transmission is independent of incidence. And that is exactly wrong for this case. Whether a photon is transmitted depends essentially on whether it is incident on the mirror. We have a contradiction. It is resolved by denying that Popper's propensity interpretation applies.

To hear all this was both exciting and familiar. It cast my thoughts back to an earlier era, to 1983, to be precise. For then, much as Isabelle did now, I had arrived as a young and hesitant Visiting Fellow to the Center for Philosophy of Science. I had walked the halls in awe at the nameplates I passed. The Director's office said "Nicholas Rescher" and I was reminded that a real person was attached to a name I had only ever known as words in a bibliography. And he might even be behind that door.

Paul Humphreys, as it turned out, was also a Visiting Fellow that year. He is now a distinguished presence, an Englishman with an impressive salt and pepper beard and the sort of accent that could get him a part as an emperor in any gladiator movie. In 1983, his beard was thicker and blacker and we were the young Turks, ready to make trouble for our seniors.

One day we assembled to hear one of our number speak. This meeting was the ancestor of our present, busy lunchtime talks. In 1983 the Center was in another building, Thackeray Hall, and our events were less well attended. The walk from the Cathedral of Learning to Thackeray Hall was just enough of a disincentive to make the difference.

I can still see Paul standing at the blackboard. He'd been thinking for a while about something not too interesting or important, he told us, and he might as well tell us about it. I settled back in my chair, still too green to recognize the detachment we philosophers of science may feign when we are worried that our proposal might just be too outrageous.

Paul then outlined his paradox.

The paradox had passed from that room to the journals and across the Atlantic and, now decades later, had made its way home to a lunchtime talk in the Center. I was pleased that I could be there to welcome it. It came in the guise of the slender Frenchwoman, who now stood before us speaking in the slow, heavily accented English that people in the US find completely charming.

She was explaining why she was not convinced that Paul's paradox was fatal after all. The resolution was mathematical and technical. I watched an elaborate translation unfold in her head: from precise mathematics to informal summaries in the language of her thought to the English of the room. Now and again, Isabelle was shocked to see a tiny typographical error in one of her formulae in Powerpoint images. She immediately assumed that her audience had seen it too. Ascribing superhuman computational powers to us, she presumed that we were already inferring massive contradictions from her claims. She carefully inscribed one corrected formula in chalk on our chalkboard.

I yearned for telepathic powers that would assure her: "Don't worry; we're not that good!"

Isabelle's resolution depended upon insisting that the inverse probability is a new probability function attached to a new system, so that the paradox producing independence is not assured. The trick was to specify a most similar system in which the inverse probability still made sense as a propensity.

I liked the formal notions, but had some trouble seeing how they worked in practice, in, for example, the original case of the photon. I pressed Isabelle in question time and again, after the talk, when we ended up in earnest conversation in the hallway, where a lot of the real business of the Center is transacted.

There is, I was now sure, a perfectly reasonable sense in which the inverse probability could make sense as a propensity without expressing the paradox generating independence. Consider a system in which some faint signal arrives and is then detected by a highly sensitive, but imperfect detector. The whole set up might be such that the detector can give spurious results, false positives that declare a signal arrives when in fact there is none.

In that case the inverse probability--of signal given detection--is now an interesting conditional probability. The same is true of its complement: the probability of no signal given that the detector announces a detection. That is just propensity of the system to yield false positives. It is quite reasonably construed as an objective property of the system of detector and its environment. There is the new system Isabelle sought; it is the original detector now considered in its environment. The paradox producing independence is gone. We would certainly not expect that the impingement or otherwise of the signal would be independent of the detector declaring a detection event.

Or at least all this seems clear to me now. The lingering worry was that somehow we were committing violence against a great causal principle that effects cannot precede causes, if we allow that the propensity of a system to produce false positives is one of its objective physical properties. Our plan tomorrow afternoon is to make Isabelle's manuscript the topic of our discussion in our Fellows reading group. I'm going to see if I can convince everyone there to treat this great causal principle with the scorn deserved by any attempt to do a priori science.

Finally I should report a moment in question time every bit worthy of the famous Monty Python "Argument skit."

Questioner [coming to a crescendo in complaints about single case probabilities]: "The difficulty with single event probabilities are that they are such a problem!"

Heckler: "That's not an objection. That's a tautology!"

Audience: Titters and groans.

Isabelle put up with this frivolity in good humor. She earned her umbrella.

John D. Norton

Isabelle Drouet
::: Propensities and Conditional Probabilities
Lunchtime talk