Hemodialysis Home Modeling Hemodialysis Therapy

Derivation of Rate Equations Example of Rate Equation Derivation

Properties of rate equations

Rate equations reveal much about how the dependent variable depends on the independent variable, usually time, without actually solving for the functional relationship between the two variables. The usual form of the derivative in a rate equation is

which is read as the rate of change of the dependent variable with respect to the independent variable.

When the independent variable is time, we can determine whether there is a steady-state region where the dependent variable does not change with time. For some types of first-order rate equations, we can use the time constant to determine how quickly the system will approach such a steady-state region. For some types of second-order rate equations, we can determine whether the approach to steady-state will be direct or will oscillate above and below the steady-state solution. Using the technique of nondimensionalization, we can determine the dimensionless groups which govern the system described by the rate equation.

Steady-State Solutions of Rate Equations

First-order rate equations describe the rate of change of the dependent variable with respect to time. The question arises whether there are regions or values for the dependent variable where it does not change with time. If such regions exist, what is the physical meaning associated with them?

Regions where the value of the dependent variable does not change with respect to time are referred to as steady-state solutions of the rate equation. As the name steady-state implies, the dependent variable value is "steady" and does not change. Occasionally, you will see a steady-state solution referred to as an equilibrium solution. When systems are at thermodynamic equilibrium, there is no net driving force (potential) and values do not change. However, steady-states can exist even where externally imposed potential differences create variations in thermodynamic variables such as temperature, pressure, or electric potential. Think about a manufacturing process that uses a conveyor belt moving through an oven. Such systems are in steady-state but not in equilibrium. Likewise, steady-state solutions are often referred to as the ultimate or limiting solution of the rate equation. This terminology results from the fact that frequently the steady-state solution occurs when time becomes infinitely great (which is indeed an ultimate or limiting value!). However, depending upon the rate equation, steady-state solutions can occur at values of time other than infinity. To avoid confusion, it is preferable to use the terminology of steady-state solution.

The steady-state solution for a rate equation can be found by employing the definition of the steady-state: a region where the value of the dependent variable does not change with time, i.e., a region where the dependent variable is constant. If the dependent variable is constant, then the derivative of the dependent variable must be zero! Thus, the steady state solution is found from

for any first-order rate equation.

First-Order Approach to the Steady-State

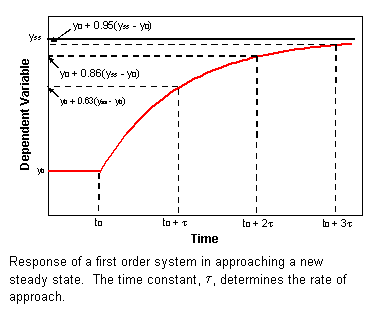Frequently, first-order rate equations can be rearranged by simple algebraic manipulations to the form

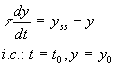
where t is referred to as the time constant and y_ss is the steady state solution. (What are the units associated with t?). This rate equation describes a system initially at steady-state y₀ that is suddenly subjected to a stimulus which causes the system to move to the new steady-state y_ss. The time response of such a system is depicted in the figure to the right. Although shown for a new steady-state at a higher value than the initial steady-state, the new steady-state could be at a lower value. The total change in the system, d, is given by the difference between the two steady-states as

The time constant determines how long the system takes to approach the new steady-state. After one time constant, the system is about 63% of the way to the new steady-state. After two time constants, the system is about 86% of the way to the new steady-state. After three time constants, the system is about 95% of the way to the new steady-state. And, after four time constants, the system is almost at the new steady-state. Thus, we can use the time constant to estimate approximately how much time will elapse before the new steady-state is achieved.

The relationship between the time constant and approach to steady-state for rate equations which can be put into the general form above comes from the analytical solution to the equation. The analytical solution is the exponential relation

(How might you show that is the analytical solution to the differential equation?) The change in y with respect to time is embodied in the exponential term

The table at the right shows the value of this term for values of time spaced one time constant apart. The last column in the table was obtained by rearranging the analytical solution to the form

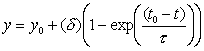
Hemodialysis Home Modeling Hemodialysis Therapy

Derivation of Rate Equations Example of Rate Equation Derivation

Copyright © 2001, John F Patzer II

All Rights Reserved