NCSA Nanotechnology InitiativeDetails of algorithmAs the number of atoms in a cluster increases, the number of local minima on the potential energy surface (PES) grows rapidly. Successful global optimization techniques must be able to escape from local basins of attraction. The GMIN algorithm1 falls into the `hypersurface deformation' category of techniques, which usually attempt to increase the rate of transition between minima by reducing the number of local minima on the PES by smoothing the surface, and therefore reducing the search space. In general, these methods rely on the assumption that the global minimum of the deformed PES will lead back to the global minimum of the original surface when the transformation is reversed. However, this is not necessarily the case, as shown by Doye and Wales.2 Wales' and Doye's GMIN algorithm avoids this problem. It transforms the PES into a collection
of interpenetrating terraces by associating the energy at any point in configuration space with
that of the local minimum found by a geometry optimization started from that
point.1
The transformed energy is given by:
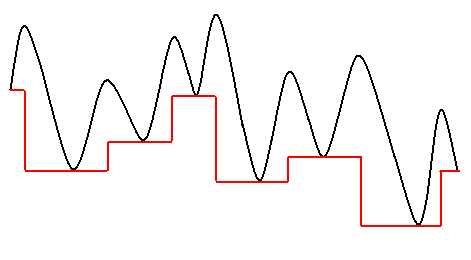
where X is the vector representing a point in nuclear configuration space and min indicates that an energy minimization, (usually either conjugate gradient or BFGS methods), has been completed starting from X. This transformation does not alter the global minimum nor the number of local minima. It simply removes transition state regions from the problem. Therefore, it is now easier to explore the transformed PES using a Monte Carlo (MC) simulation since areas separated by barriers on the original PES are now only separated by steps between the energy levels of the minima. The system can hop directly between basins of attraction at each MC step (`basin hopping'). This schematic illustrates the way GMIN might change a potential (black) into a modified "terrace" potential (red).
Previous applications of the GMIN basin-hopping algorithmThe GMIN algorithm has been successfully used to locate the global minima of Lennard-Jones (LJ) clusters with up to 110 atoms, including the face-centered-cubic truncated octahedron for LJ38,1 which has proven particularly difficult to locate using unbiased searches. In addition, the global minima of clusters containing up to 80 atoms modeled by both the Morse2 and Sutton-Chen families of potentials3 have been found. More recently, the global potential energy minima for (NaCl)nCl- have been identified using this global minimization approach.4 A recent analysis5 of why the basin-hopping or MC minimization method is so successful concluded that there were two key features:
|
Dept. of Chemistry, University of Pittsburgh,
219 Parkman Avenue, Pittsburgh, PA 15260
Phone: (412) 624-8690 FAX: (412) 624-8611 email: jordan at pitt.edu
This page last updated: