| HPS 2626 Phil 2626 |
Topics in Recent Philosophy of Physics | Fall 2013 |
Back to course documents.
Warm Up Exercises
1. An ideal gas of n molecules expands reversibly and isothermally from a volume V to a volume 2V. What is the work done by the expanding gas on the piston?
2. Recalling that the internal energy U of an ideal gas depends only on its temperature and not volume, what is the heat gained by the gas during the expansion?
3. In the process of 1. and 2., (a) What is the change thermodynamic entropy of the gas? (b) What is the change of thermodynamic entropy of the environment?
4. An ideal gas of n molecules at temperature T is held in a balloon of volume V. The balloon pops so that the gas expands to fill a chamber of size 2V. (a) What is the change thermodynamic entropy of the gas? (b) What is the change of thermodynamic entropy of the environment?
A canonically distributed thermal system at temperature has a phase space γ with canonical position and momentum coordinates x and p. That means that the propbability density for the system being found at x and p is proportional to exp(-H(x,p)/kT), where the system Hamiltonian is H(x,p) and K is Boltzmann's constant.
1. What is the system's partition function Z(γ)?
2. Let γsub be some subspace of the system's phase space γ. What is the probability that the system will be found in that subspace?
3. What is free energy F in terms of internal energy U, entropy S and temperature T? How is it related to the partition function Z(γ)?
(from Tom Pashby)
1. Verify that the standard (position) representation of the position and momentum operators,
(Q)(f(x))= (x)(f(x)), (P)(f(x))=(-id/dx)(f(x))
implies the canonical commutation relation [Q,P]= i. On what domain of functions does this relation hold?
2. Show that the Weyl CCR,
implies the covariance of Q with shifts in its spectrum,
i.e. .
Does this apply to P as well?
Hint: the spectral resolutions of Q and
are
or, in bra-ket notation:
and
3. (Bonus extra credit) Show that the Weyl CCR implies the Heisenberg CCR [Q,P] = i. Does the implication go the other way?
(Hint: Stone's Theorem says that every unitary group of the form has a unique self-adjoint generator A.)
(NB: We are using natural units where ℏ=1.) [Also, the signs may not be correct.]
Consider the differential equation d2r/dt2 =√r. For initial conditions, r(0) = dr(0)/dt =0:
1. Show that a solution is r(t) = 0, all t.
2. Show that a solution is
r(t) = 0 all t ≤ 0
r(t) =(1/144) t4 all t ≥ 0.
1. A point charge is the sole cause of the electric field that surrounds it. How does Curie's principle limit the disposition of the electric field in space?
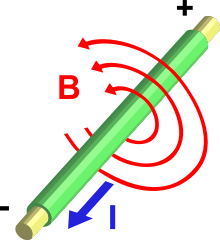
2. Oersted found that an electric current I creates a magnetic field B in the neighborhood of the conductor that obeys the right hand rule (current points in direction of thumb; field in direction of fingers of curled right hand). If the current is the cause of field, does this configuration conform with Curie's principle? Doesn't the principle require that the magnetic field lines run parallel to the conductor?
In preparation for this meeting, write down two questions that you will use to initiate discussion with him.
In addition to readings in the seminar, you may find his website or wikipedia article helpful.