| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
What use is spacetime? It turns out to make visualizing and understanding the relativity of simultaneity a great deal easier. The judgments of simultaneity of different inertial observers correspond to slicing the spacetime up into different stacks of spaces with each space formed from a set of simultaneous events.
To see how this works, here are three observers in relative motion in a spacetime.
| First we have an observer whose worldline runs vertically up the page. |
| The next observer moves to the right with respect to the first. |
| The third observer moves to the left
with respect to the first. |
Notice how differently they slice up the spacetime into spaces of simultaneous events. That difference simply is the relativity of simultaneity. It is expressed in the tilting of the hypersurfaces of simultaneity as we move the judgments of simultaneity of events from inertial observer to inertial observer.
In looking at the three slicings as they are drawn above, it is easy to fall into the trap of imagining that the first slicing is somehow the "right" one and the second and the third are distortions due to the observers' motion. That would be a mistake. The principle of relativity assures that all three observers are equally good. The judgments of simultaneity of any one is just as good a those of the other two and each of the figures is an equally good way of dividing the spacetime into sets of simultaneous events.
The fact that one observer's worldline is drawn as a vertical line and the others are oblique is just an accident of the way we chose to draw the diagram. Correspondingly, the fact that one observer's hypersurfaces are perfectly horizontal and the others are tilted is again an accident of the way we drew the figure. We could redraw the figures so that the third observer's worldline, say, is vertical. Then the third observer's hypersurfaces of simultaneity would be drawn as horizontal; the worldlines of the other two observers would be diagonals; and their hypersurfaces of simultaneity would be tilted.
The situation is the same in general principle as with maps of the world. We are used to maps that show North at the top of the map. The placement of North does not reflect any geographical necessity that North somehow is truly "on top." We could equally draw a map of the world with South at the top. The geographical facts conveyed by the two maps are same in both maps. When we read the map, we just ignore the fact that North is commonly at the top since it represents no geographical fact. It is just an artifact of how we chose to represent those facts on a paper map.
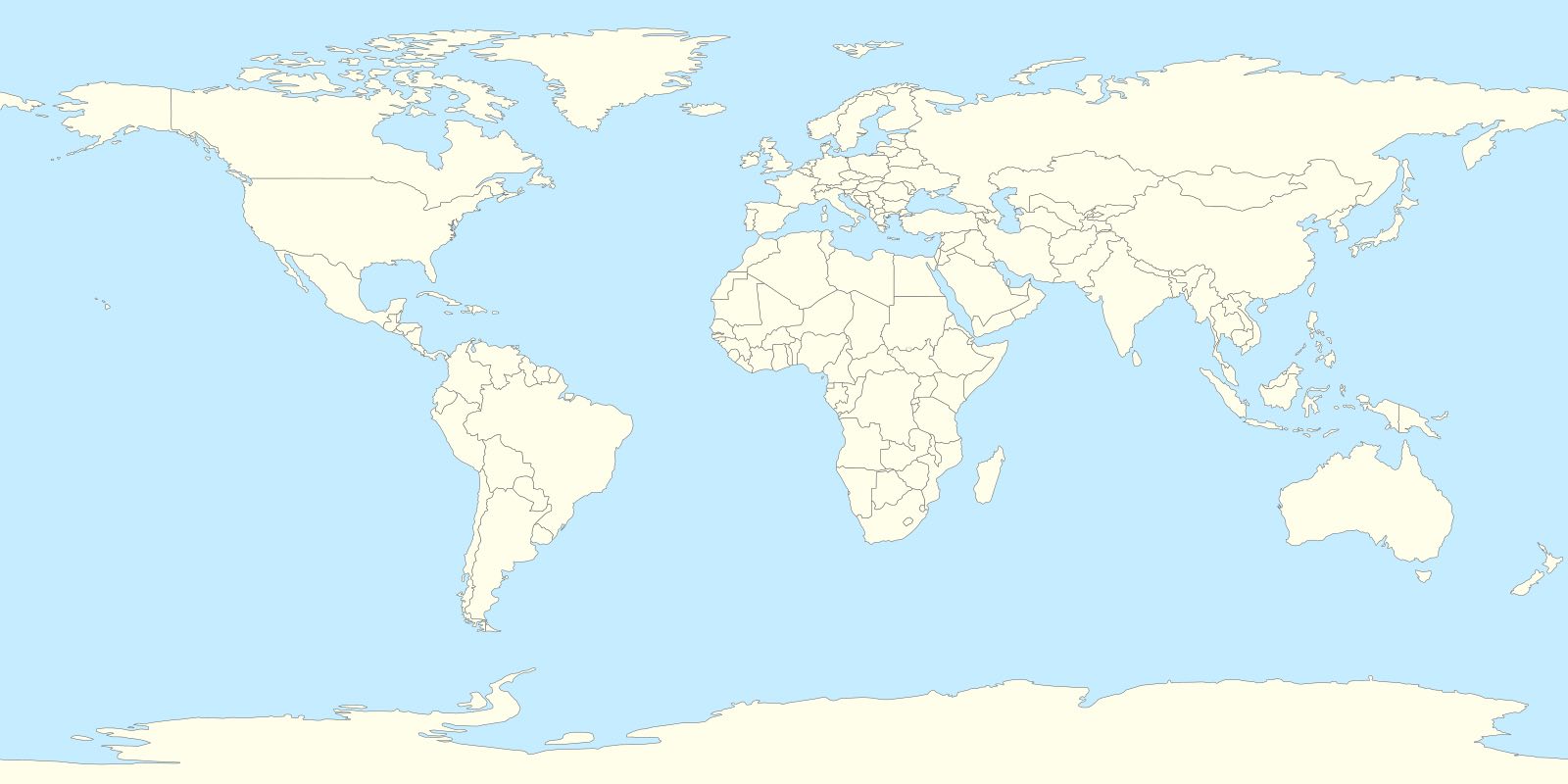
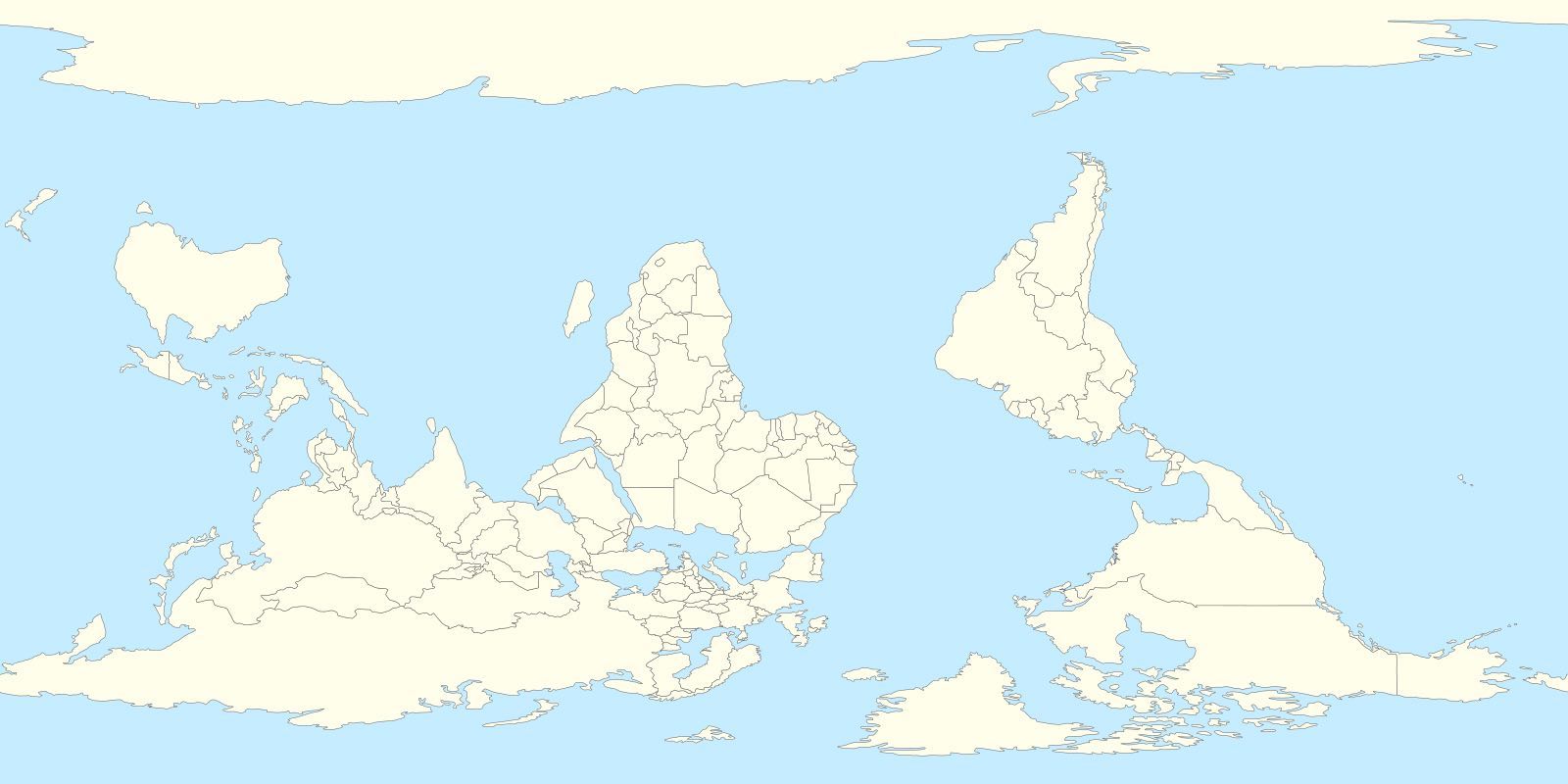
Public domain map.
https://commons.wikimedia.org/wiki/File:World_location_map.svg
| Two points to watch
when you are drawing this tilting of hypersurfaces.
First, setting an observer into motion to the right will tilt the observer's world line to the right; and the hypersurface of simultaneity will also tilt up on the right side to meet it. Second, if one follows the usual convention of drawing light lines at 45o, then the angle of the observer's worldline to the vertical will be the same as the angle of the hypersurface of simultaneity to the horizontal. |
The tilting of the hypersurfaces gives us a simple picture of how inertial observers in relative motion assign times to events.
| An inertial observer carries a clock that marks
the time of events along the observer's worldline as "1," "2," "3,"
... That settles the time of events only on the worldline for the
observer. What time should be assigned to events
not on the observer's worldline? The observer's
hypersurfaces of simultaneity answer. Consider the hypersurface that passes through the event of the clock showing "1." All these events are simultaneous in the judgement of the observer. Therefore all these events are assigned time "1. The same applies for the remaining hypersurfaces that pass through the events of the clock ticking "2" and "3." All the events on those hypersurfaces are assigned times "2" and "3," respectively. |
| The same analysis
obtains for a new inertial observer who moves relative to the
original observer. The new observer's clock assigns times to events
on the observer's world line. The observer's hypersurfaces of
simultaneity are then used to propagate the times throughout the
spacetimes. Clearly the original and new observer will differ on the times each assigns to the same event in almost every case. Is there a sense in which one is assigning times correctly and the other not? There cannot be. The principle of relativity requires each observer's frame to be equivalent. If the procedure is good in one inertial frame, then it is equally good in all. This reminds us once again that there is no frame independent notion of simultaneity in a Minkowski spacetime. |
Just why is it that hypersurfaces of simultaneity tilt when we change the state of motion of the observer or reference frame? A simple construction in spacetime geometry shows how it comes about.
The construction represents a physical procedure for identifying simultaneous events using light signals in a familiar way. An inertial observer stands at the midpoint of a large platform. the observer sends out two light signals, in opposite directions. They are reflected back to the observer by mirrors at each end of the platform. The light signals arrive back at the observer at the same moment.
Since the observer is at the midpoint of the platform and the signals arrive back at the same moment, the observer infers that the two reflection events occurred simultaneously. Call these events A and A'. By placing the mirrors at other positions on the platform, the observer can use the procedure to determine other pairs of simultaneous events, B and B'; and C and C'; and so on. These judgments of simultaneity enable the observer to map out a full set of simultaneous events that form a hypersurface of simultaneity.
| The figure opposite depicts this procedure in a spacetime
diagram. We represent the inertial trajectory of this
inertial observer by a timlelike worldline, drawn vertically in the
diagram. Light signals leave the observer at the same moment, are reflected at event A and A' and arrive back at the observer's worldline at the same moment. The observer can then infer that the reflection events A and A' are simultaneous and lie on the same hypersurface of simultaneity. This same reasoning applies to the remaining events shown in the figure: B', C', B and C. They are produced by reflections from mirrors suitably located at other positions on the platform. The observer judges B and B' to be simultaneous; and C and C' to be simultaneous. If the emission of the light signals for reflections B/B' and for C/C' are suitably delayed (as shown), then all six of these events will lie on the same hypersurface of simultaneity that passes through the event O on the observer's worldline. The are thus simultaneous with O. The totality of simultaneous events like these form a flat plane perpendicular to the observer's worldline. |
The light signals reflected at A' and A arrive back at the observer at the same time. That they must do this is obvious from the symmetry of the procedure. The light signals left the observer at the same moment. They are reflected back after they have traveled the same distance. Therefore they must arrive back at the same time. If they did not arrive back at the same moment, something would clearly have gone wrong in the procedure. This remark will become important in a moment!
Now consider a second case in which a new inertial observer moves relative to the original inertial observer. The new observer's worldline will be drawn below as a tilted line. Which events will that observer judge as simultaneous with an event O on that observer's worldline?
Although the worldline is now tilted, the same procedure just described can also be used to pick out the events simultaneous with O. Indeed the principle of relativity requires this, for otherwise we would have some intrinsic difference between the first inertial frame and the second; only in the first could this procedure be used.
| The construction proceeds as before and it is
drawn on the left. As long as we adhere to the light
postulate and draw the lightlike curves at 45 degrees to
the vertical, we will end up plotting out events A', B', C', A, B
and C that lie on a tilted hypersurface. This happens because the emission and return events for the light signals have been displaced to the left and right respectively. We now need to locate the bends in the lightlike curves--the reflection events--in such a way that, as before, the light signals from A and A' return at the same arrival event (and so also for B and B' and for C and C'). That can only happen if we displace the reflection events into the tilted hypersurface shown. |
It may be obvious to you that the hypersurface of
simultaneity has to tilt in the way shown for this procedure to
work. If not, the remedy is to draw the construction for yourself.
To help you, here are the steps. How do we arrive at this background? If special relativity is correct, it is a matter of measurement and observation. Using rods, clocks and light emitters, we would map out the trajectories taken by light signals and the proper time and distance separating pairs of events. When the investigations are complete, we would recover the figure shown. |
|
| Using the these background lines to guide the
placement of the lightlike curves, here is the procedure for the first
frame of reference. The worldline of the observer is drawn as a vertical line E to E'. Two light signals are emitted at the event E on the observer's worldline. They propagate to events A and A'. They are reflected back to the observer at each of these events. They arrive back at the observer at the same time, at event E'. As noted above, the critical element is the success of the procedure is that both light signals return to the observer at the same moment at event E'. Then the observer can infer that the event O is simultaneous with the two events A and A'. |
|
| Now let us consider the case of the moving
observer. Here the worldline of the moving observer
inclines to the right. If we try to carry through the construction representing the procedure without inclining the hypersurface of simultaneity, we run into trouble. Two light signals are emitted by the observer at event E as before. They propagate to the two events A and A' on the untilted hypersurface of simultaneity. They are reflected at these events back towards the observer. However it is clear from the figure that they cannot return to the observer at the same moment. The procedure fails to affirm the simultaneity of A and A' for this observer. |
|
| The observer must seek other events A and A'
for the procedure to succeed. A suitable choice is shown opposite.
It arises from tilting the hypersurface of simultaneous events
passing through A and A'. With this choice of events, the light signals reflected at A and A' return to the observer at the same moment, at event E', as required by the procedure. |
There is another related way to see why we must tilt the hypersurfaces of simultaneity. Consider the case of a light signal bouncing to and fro along an inertially moving rod. Observers moving with the rod must judge the forward and return travel time to be the same. An inertial observer, moving relative to rod along its length, will judge these times to be unequal. For this to happen, the hypersurfaces must be tilted. The details are in the next chapter here.
We can use spacetime diagrams to give us a much simpler, geometric picture of how it is possible that two moving observers can each judge the other's clocks to have slowed. The set-up employs just half of the construction that is used in the twin effect to be described below. So I call it the "half twin effect."
We imagine that twins A and B set off in inertial motion at the same speed but in opposite directions with respect to our vantage point on earth. Each twin carries a clock. As they move away from each other, each twin judges the rate of the other's clock. How this is done is a detail we need not fuss with. They might use light signals, for example, and correct for the time of flight of the signals to figure out what was the other twin's clock reading at each instant.
Since the arrangement is symmetric, we expect that each will make the same judgment about the rate of the other's clock. That sameness might just be that each judges the other's clock to run at the same rate as their own. This is the case we might expect if we let classical Newtonian physics guide us. Or each might judge the other's clock to have slowed; or that it has sped up. Whatever judgment A may make of B's clock, then B will make the same judgment of A's clock.
If we draw a spacetime diagram of the arrangement, we can just inspect it and read off the result according to the special theory of relativity. Each will judge the other's clock to have slowed; and the spacetime diagram shows that there is nothing paradoxical in this result. (The clock readings are the numbers next to each twin's worldline.)
Twin A wants to determine the rate of B's clock. Twin A will note that both twins' clocks had the same zero reading when they began their outward journeys. Then twin A asks: when A's clock reads 1, 2, 3, 4, ... what does B's clock read? Answering requires that A make judgments of distant simultaneity. To do this, A must use the hypersurfaces of simultaneity appropriate to A's motion. Because of the way those hypersurfaces tilt, A will judge B's clock to read earlier times. For example, when A's clock reads "4," twin A will judge that B's clock reads only "3." As a result, twin A will judge that B's clock runs slower. For 4 units of time have elapsed on A's clock, while only 3 have elapsed on B's clock.
Twin B will give the same analysis. However, since twin B is in motion relative to A, twin B's analysis will make different judgments concerning which events are simultaneous. These different judgments are represented by B's hypersurfaces of simultaneity. When B's clock reads "4," twin B will judge A's clock to read only "3." As a result, twin B will determine that A's clock runs slower.
Thus each infers that the other twin's clock is running slower. Of course, an observer on earth with our vantage point finds the twins to recede with equal speed in opposite directions and would judge that the rates of both twins' clocks to be the same.
We may wonder if things will work out the same way if the twins approach rather than recede. Will each judge the other's clock to have slowed? Or, since they are now approaching each other, will they judge the other's clock to have sped up?
Drawing the spacetime diagram (below) once again shows the result according to relativity theory. Each will still judge the other's clock to have slowed. In the diagram, it is convenient to count down the times read by A's and B's clocks as -4, -3, -2, -1, 0, so both clocks read zero when the twins meet at the same event.
Twin A use's A's hypersurface of simultaneity to determine
that, when A's clock reads "-4" ,B's clock reads "-2". When the twins
meet, both clocks read "0". Hence twin A infers that 4 units of time
passed on the A clock, while only 2 units
passed on the B clock. Hence twin A infers that the B clock runs slower
than the A clock. Twin B makes the corresponding inference about the A
clock.
Essentially the same analysis applies to relativistic length contraction. Each of the observers A and B carry a rod, where the rods have the same length when compared in one frame of reference. Each observer will judge the other's rod to have contracted. That is puzzling until we recognize that each of these judgments makes essential use of a judgment of simultaneity. Once again, when we take into account how the observers' judgments of simultaneity differ, we can see how each ends up judging the other's rod to have shrunk.
Setting things up is a little more complicated, because measuring length is more complicated than comparing the time read by clocks. We start with two rods, A and B, moving in opposite directions. We then ask how observers moving with each would judge the length of the other rod. The most direct way is for observer A to have a very long ruler that is at rest with respect to A and long enough to reach the other rod B. The B rod will be moving along A's ruler. Observer A arranges for a measurement of the B rod's length using the procedure described in an earlier chapter. Similarly, observer B will have a very long ruler that extends all the way to the A rod and will use it to measure the length of the A rod.
This arrangement is shown in the figure. The A rod and observer A's ruler are moving together to the left. The length of the A rod is unity, as measured on A's ruler. Similarly, the B rod and observer B's ruler are moving to the right. The length of the B rod is unity as measured on B's ruler.
What length will observer A judge for rod B? It is hard to tell from the ordinary space figure above. The B rod is somewhere around the 6 and 7 marks on A's ruler. But since the B rod is moving rapidly over observer A's ruler, we need to proceed carefully. To know exactly what length observer A would find, we would need to know how the two ends of B's rod align with the marks on A's ruler at the same moment. That crucial condition--"at the same moment"--is where A's judgments of simultaneity enter. Precisely the same considerations apply for observer B's assessment of the length of the A rod.
A spacetime diagram lets us see at leisure how these
crucial judgments of simultaneity enter. The diagram shows the worldlines
of the two ends of observer A's rod. The rod itself and the long ruler
carried by A are also shown. They are shown at one
instant, corresponding to a hypersurface of simultaneity of
observer A's frame of reference. Observer B's rod and ruler are shown in
corresponding fashion.
As before, the symmetry of the figure already
shows that whatever observer A finds for the B rod, observer B will find
for the A rod. So if observer A judges the B rod to have shrunk, observer
B must judge the A rod to have shrunk. But will observer A judge the B rod
to have shrunk?
Observer A judges the length of a rod by checking where the worldlines of the ends of the rod intersect with A's ruler. These intersections are events in spacetime. The essential condition is that these intersection events happen at the same time; that is, they are simultaneous. The ends of the A rod intersect with observer A's ruler in the two simultaneous events shown in the figure below as the two small red circles on the left. (Remember: they are simultaneous events since they lie on one of observer A's hypersurfaces of simultaneity.) These two events are at the 1 and 2 mark on the ruler, affirming that observer A will judge the A rod to be of unit length.The ends of the B rod intersect with observer A's ruler at the two events marked by red circles on the right. These two events lie between the 6 and 7 marks on observer A's ruler. Hence observer A will judge the B rod to be shorter than unity in length. That is, observer A will judge it to have shrunk.
Observer B will carry out an analogous
analysis and judge that the B-rod is of unit length, but that the A-rod is
shorter than unit length. Below is the figure showing the corresponding
intersection events for observer B's measurements of the lengths of the A
and the B rod.
Just what is so special about a Minkowski spacetime? One might think that it is the idea of representing space and time together in a four dimensional geometry, where the four dimensionality of the geometry outstrips our immediate powers of visualization. It is certainly the case that the four dimensionality is both interesting and hard to visualize. But there is nothing inherently relativistic about it. One can take all the physics of Newton and re-express it in four dimensional terms.
The big difference between Newtonian and relativistic spacetimes lies in how they are sliced up into three dimensional spaces. That slicing is done by picking out sets of simultaneous events to form three dimensional spaces.
In Newtonian spacetimes, there is only one way to do this, so a Newtonian spacetime unstacks into a unique set of spaces. In this sense, space and time remain distinct even if we represent the physics in a spacetime.
In a relativistic (i.e. Minkowski) spacetime, the relativity of simultaneity tells us that there are many ways to do this; there is no unique, preferred unstacking. In this sense, space and time get fused together and this fusion is the real novelty of the spacetime approach in relativity theory.
This novelty is surely what Hermann Minkowski had in mind when he wrote in the introduction to his famous lecture "Space and Time" of 1908:
 |
"The views of space and time which I wish to lay before you have sprung from the soil of experimental physics and therein lies their strength. They are radical. Henceforth space by itself and time by itself, are doomed to fade away into mere shadows, and only a kind of union of the two will preserve an independent reality." |

Copyright John D. Norton. January 2001, September 2002; July 2006; February 3, 2007; January 23, September 24, 2008; February 2, 2010; February 7, 2012. November 5, 2016. January 31, 2017. Typo corrections, September 14, 2020. February 3, 2022. February 1, 2024.