
http://en.wikipedia.org/wiki/File:Old_book_bindings.jpg
| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
The arrival of Einstein's general theory of relativity marked a rebirth of interest and work in cosmology, the study of the universe on the largest scale. Within Newtonian theory, cosmology had reduced essentially to one question: just how is matter distributed within an infinite, Euclidean space. Einstein's theory made the question much more interesting. For now cosmologists had to contend with many possible matter distributions, many possible geometries and many possible dynamics for both.
What connected all these together was Einstein's gravitational field equations. They specified just which matter distributions could go with just which geometries and how the whole system might evolve over time. One way to think of these equations is as a law that our universe must satisfy. Another is to imagine them as a selection rule. Among all conceivable universes, only some will satisfy Einstein's equations. These universes are the ones that we designate as possible universes, where "possible" now just means "licensed by Einstein's theory."

http://en.wikipedia.org/wiki/File:Old_book_bindings.jpg
| I like to think of these possible universes as each comprising a page of a great book. Metaphorically, Einstein's gravitational field equations are that book. We shall now turn to reading that book. Just what sorts of universes are possible according to Einstein's theory? As we flip from page to page we will see some quite interested universes. Among them we hope to find our own. |
Minkowski spacetime is the spacetime in which special relativity holds. This is the simplest all solutions of Einstein's equations. It is the case of no gravity. It arises in when the unsummed curvature of spacetime is zero. What that means is this: if we test for curvature in all possible directions of the spacetime sheets, we find no curvature in each of them. We assemble all these zero results and write them collectively as:
|
(UNsummed)
curvature
of spacetime |
= | 0 |
This is the unsummed curvature. The summed curvature that arises in Einstein's gravitational field equations comes from adding up these individual curvature terms in a way specified by the Einstein tensor. Since we are adding up many zero terms, we know that the result of the additions must still be zero. That is, if the unsummed curvature is zero, then the summed curvature must also be zero.
|
Summed curvature
of spacetime |
= | 0 |
Einstein's equations tell us that this summed curvature equals the matter density. Therefore they will be satisfied if the universe is free of matter. For this reason, Minkowski spacetime is an unrealistic candidate for our universe. We know our universe has matter in it!
A Minkowski spacetime is still physically relevant to our spacetime, however. The situation is similar to one we encounter on our earth's surface. We know that this surface is a sphere in the large and that a non-Euclidean geometry must be used to analyze it.
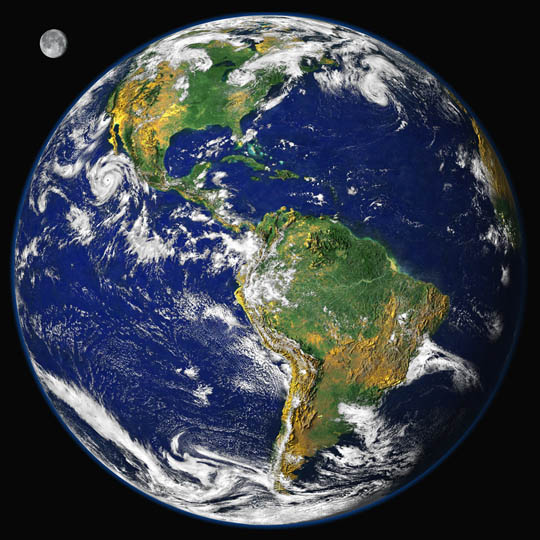
"Blue marble" image from NASA
http://eoimages.gsfc.nasa.gov/images/imagerecords/54000/54388/BlueMarble.jpg
Yet in any small patch--such as an area of land the size of a city--we can ignore the curvature and apply Euclidean geometry without appreciable error.

New York city street grid. (From Google
Maps.)
Correspondingly, for many applications, Minkowski spacetime is a sufficiently good approximation in the small.
It will fail, however, whenever, gravitation is strong; that is, when the curvature is large. In the vicinity of the sun, gravitation is not strong. So there we manage to extend the use of Minkowski spacetime by pretending that curvature effects of gravitation are really due to a new field, the gravitational field.
The more interesting spacetimes come from other pages of Einstein's book. We find them by "solving" Einstein's gravitational field equations. That just means that we find spacetimes whose summed curvature matches the matter density in the precise way that Einstein's field equations demand. The activity is called "solving" since it is the same as what is done in algebra. You write an equation for some unknown quantity "x" and solve the equation for x. The resulting value of x is called the "solution."For example:
2x
+ 1 = 5
2x + 1 -1 = 5 - 1
2x = 4
2x/2 = 4/2
x = 2
In solving the Einstein equations, however, we are writing equations for an unknown universe. When we solve them, the solution is an entire universe.
Sometimes, we write algebraic equations that have more than one solution. For example:
x3 - x = 0
is solved by
x = 1 and x=-1
and x=0.
We might deal with the multiplicity of solutions by saying the we are only interested in positive number solutions. Then we have a unique solution, x=1.
Having multiple solutions is commonly the situation with the Einstein equations. We narrow down the solutions to a few or one in each case by adding extra conditions. We may only be interested in spacetimes that are geometrically the same everywhere (i.e. they are "homogeneous"). Or we may only be interested in solutions that become Minkowskian very far from matter. These extra conditions are known loosely as "boundary conditions," since they are most commonly used to stipulate how the spacetime must be at some boundary such as spatial infinity.
Minkowski spacetime is the simplest solution. Finding others is a formidable mathematical challenge and only the simplest of solutions are easy to find. So when a new solution is found, the new solution is generally named after whoever found it. Finding a solution is really discovering a new, possible universe. So the discoverer's name is then attached to that universe: an Einstein universe, de Sitter spacetime, A Goedel universe, a Reissner-Nordstroem spacetime, and so on.
While the activity of solving Einstein's equations is very hard, the process in conceptual form is quite easy to describe. The Einstein equations specify how spacetime can be locally, that is, at any one point. They say this much curvature always goes with this much matter. To solve the Einstein equations is merely finding a way of distributing curvature and matter over spacetime so neighboring points mesh correctly.
| A rather good analogy is to the solving of a jigsaw puzzle. The Einstein equations give us an endless supply of small pieces. They are how spacetime can be in infinitesimally small patches. Each piece has the right combination of curvature and matter. |
|
Solving the Einstein equations corresponds to finding a
combination of pieces from the supply that can be fitted
together. |
| The simplest possible solutions are "homogeneous"--that means that they are everywhere the same. In the jigsaw puzzle analogy, that means that the spacetime has to be put together from repetitions of the same piece over and over and over. In the case of a Minkowski spacetime, that piece is just one that has no curvature and no matter. |
| This was one of the first interesting, exact
solutions given for Einstein's equations and was computed by the
German astronomer Karl Schwarzschild. It is of a universe which
looks like a Minkowski spacetime as you get close to infinity in
space. It has a central point in space
around which all the curvature is distributed symmetrically. It is
unchanging in time. The conditions then pick out the solution
uniquely. This spacetime is taken to be a good approximation for the spacetime around the sun (as long as we neglect that the sun rotates and has some electric charge). Even this simple case was difficult to solve. Einstein himself had not found the exact solution for the spacetime surrounding the sun in his work of November 1915. He had then computed the motion of Mercury from an approximation. Schwarzschild found the exact solution and communicated it to Einstein in a letter of December 22, 1915. The story is tragic. All this happened during the First World War. Schwarzschild was serving in the German army at the Russian front when he found the solution and wrote to Einstein. He died at the front on May 11, 1916. |
 |

http://photojournal.jpl.nasa.gov/jpeg/PIA01936.jpg
In the jigsaw puzzle analogy, the solution is put together from pieces that are flat like those of the Minkowski spacetime in regions that are far from the central point. The pieces get more curved as we approach the central point, but their curvature always respects the rotational symmetry of the space around the sun.
The Schwarzschild spacetime is a good approximation of the spacetime around our sun. But does it work for the whole universe? It would work if all the matter of the universe were located in just one island in an otherwise empty space. However, when Einstein started to contemplate these possibilities shortly after completing his general theory of relativity in 1916, he did not like this possibility for two reasons.

http://photojournal.jpl.nasa.gov/jpeg/PIA07905.jpg
First, the astronomical information available to Einstein at that time indicated that the universe was filled with a roughly uniform distribution of stars. So empirically, the model was wrong.
Second, there was a deeper theoretical worry. General relativity had shown how matter fixes the summed curvature of spacetime. Einstein liked that notion a lot. It reduced the arbitrariness of a spacetime. Why did the geometry curve this way here and that way there? It did so because the matter distribution went this way here and that way there. The theory reduced the number of arbitrary stipulations that needed to be made in building a picture of our spacetime.
Einstein liked this idea so much that he elevated the idea to a principle. He demanded that the whole geometry of spacetime must be fixed by the matter distribution. That is stronger than what he had up to then in his field equations. For the Einstein equations only required the matter distribution to fix the summed curvature at each event in spacetime. One value of a summed curvature can correspond to many values of the unsummed curvature.
That possibility left a freedom in the geometry that Einstein now wanted to eliminate. The matter distribution would have to override this freedom. The matter distribution, he insisted, must fix the geometry completely. In 1918, Einstein called this stronger requirement "Mach's principle," since it reminded him of epistemological analyses of space and time undertaken by the physicist-philosopher Ernst Mach.

This page of Ernst Mach's celebrated Science of Mechanics has Mach's classic commentary on Newton's bucket. It is the principal source for what became "Mach's principle."

In his masterpiece, Principia, Newton had considered a rotating bucket of water. Centrifugal forces drive the water in the bucket up the sides of the bucket, so that the water surface becomes concave. Newton argued that this effect is due to the rotation of the water in the bucket with respect to absolute space. A modern version of Newton's point can be made with a fair ground chain carousel. As the carousel spins, the riders are flung outward by centrifugal forces. In Newton's account, this effect is due to the riders' rotation with respect to absolute space.

https://pixabay.com/photos/folk-festival-chain-carousel-3422752/
Mach was gravely troubled by the idea of absolute space itself. It is not something accessible to observation. So he redescribed the situation in terms of what is observable. All we know, he told us, is that these centrifugal forces arise when there is a rotation with respect to the other masses of the universe. As the riders rotate, they are rotating with respect to the stars. We now have an account of the process that makes no mention of absolute space. It is all given in terms of what we can observe.

Einstein was greatly inspired by Mach's analysis. In his hands, the idea became that the centrifugal forces were caused by rotation with respect to the stars, that is, by all the other masses of the universe. Since centrifugal forces arise when a body deviates from inertial motion, Einstein took this to mean that these other masses of the universe determine which are the inertial motions here at the carousel. More generally, these masses determine the entire spacetime geometry here at the carousel. That idea is "Mach's Principle" mentioned above.
We have already seen the role this idea played in Einstein's earlier discovery of general relativity in form of the "relativity of inertia." Then he illustrated the idea with his thought experiment of two spheres.

| Einstein was committed to these ideas well before general relativity was completed. With its completion, they took on a new urgency, especially in the case of a Schwarzschild spacetime. The difficulty is that a Schwarzschild spacetime has a property that is not fixed by the matter distribution. That is its flatness at spatial infinity. There is no matter in realms remote from the center of the spacetime, so there is no matter to determine that flatness. It is something that we have to demand in addition. |
In the jigsaw puzzle analogy, the problem is this: near the center, we know that we need to lay down pieces of spacetime that respect the rotational symmetry of spacetime around the central mass. But when we get far away from that central island, what sorts of piece are we supposed to lay down? In a Schwarzschild spacetime, we lay down pieces that look more and more like those found in a Minkowski spacetime. But that is now a choice we are making. Nothing about the matter in the central island forced us to make it. That arbitrariness is what worried Einstein.
 |
If you have been reading attentively,
you will have noticed that I have been careful to say only that
this arbitrariness worried Einstein. It is not clear that
we should we worried about this arbitrariness.
Historically, Einstein's imagination was grasped by the idea of
the matter distribution fixing spacetime geometry completely. It
would be a pretty outcome and one that Einstein found very helpful
in guiding his construction of new theories. If those theories
survive empirical testing, we might even discover that his idea
happens to be true. Somewhere, somehow Einstein came to believe
not just that it might happen to be true. He came to believe that
it has to be true. This is a much
stronger claim. In retrospect, it hard to see how to justify it.
What if the matter of the universe were all collected in one big
central island. What is wrong with spacetime remote from the
island being flat? The universe has contingent features. Why can't
that be one of them?
Einstein eventually lost his enthusiasm for Mach's principle. Writing much later in 1946 for his Autobiographical Notes, he gave this farewell to the principle: "Mach conjectures that in a truly reasonable theory inertia would have to depend upon the interaction of the masses, precisely as was true for Newton's other forces, a conception that for a long time I considered in principle the correct one. It presupposes implicitly, however, that the basic theory should be of the general type of Newton's mechanics: masses and their interaction as the original concepts. Such an attempt at a resolution does not fit into a consistent field theory, as will be immediately recognized." |
How could one avoid the need to stipulate the properties of spacetime at infinity? In 1917, Einstein came up with an ingenious escape: obliterate spatial infinity!

By adding an extra term to his gravitational field equations, Einstein found a simple solution of his augmented field equations. ("Augmented"? What is that about? It refers to the famous λ. See below for an explanation.) It contains a uniform matter distribution that approximates a uniform distribution of stars. That matter is at rest and the geometry of a spatial slice is unchanging with time. Space, however, curves back onto itself so that it is spherical. That is, space has the geometry of 5NONE with positive curvature. In such a space, there is no infinity at which to stipulate the properties of space and time.
If one pictures just one dimension of space, then the universe looks like a cylinder. Spacetime resides just in the surface of the cylinder. The vertical lines are the world lines of the stars at rest. The one spatial dimension is wrapped back onto itself; the time dimension is not. Each spatial slice at a particular time appears as a circle; if we could represent all three dimensions of space, we would somehow have to replace the circle by a complete sphere of three dimensional space.
The Einstein universe is an especially simple universe. It is homogeneous. That means that, like Minkowski spacetime, it is geometrically the same at every event. It is also spatially isortropic, which means that it is the same in every spatial direction. In the jigsaw puzzle analogy, this homogeneity means that the spacetime is assembled from just one sort of piece, used repeatedly to build the entire spacetime.
Something important passed by rather quickly just now. The Einstein universe turns out not to solve Einstein's gravitational field equations of 1915. In order to accommodate the new cosmology, Einstein had to make what appeared to be a somewhat arbitrary adjustment to his gravitational field equations.
In their original form, they said
|
summed curvature
of spacetime |
= | matter density |
We saw in the chapter on general relativity what these equations require inside a uniform matter distribution. That was our first illustration--masses falling in an evacuated tube inside the matter distribution of the earth. There we saw that there is a positive curvature in the space-time sheets of space time that makes the masses accelerated towards each other.
| The situation is the almost exactly the same as with objects within the uniform matter distribution of the Einstein universe. Einstein's original gravitational field equations call for positive curvature in the space-time sheets. That means that his field equations are calling for the same sort of dynamics as we saw for masses falling freely in a tube drilled through the center of the earth. All the matter of the universe should be accelerating towards the other neighboring pieces of matter, just as the neighboring masses in the tube accelerate towards each other. That is, all the matter of this universe should be undergoing everywhere an inward gravitational collapse, perhaps delayed only by an initial outward velocity. | This difference between this case and the hole in the earth is that the matter of the earth is prevented by the mechanical incompressibility of rock from going into the free-fall motion of of the masses in the tube. The stars comprising cosmic matter are not kept apart by an incompressibility and thus should accelerate towards each other. |
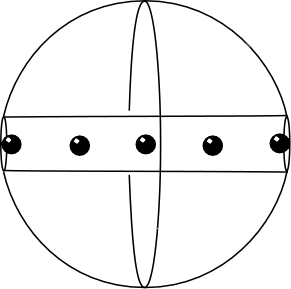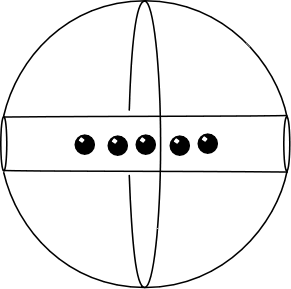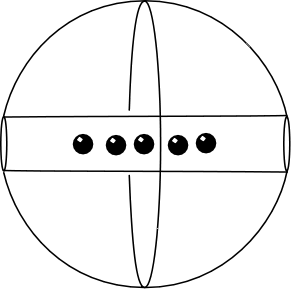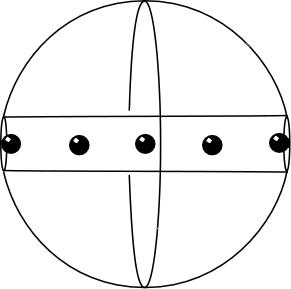
The trouble is that there is no curvature in those sheets in an Einstein universe; the spatial slices remain unchanged through time. There is no convergence or divergence of the points of the matter distribution.
Einstein's resolution was to modify his field equations in a way that would no longer call for this particular curvature. That is, he put another term into the equations that supplied the missing curvature. The real justification was essentially only that it gave him the result he wanted, the admissibility of his new universe. The term added was Einstein's celebrated "cosmological term" or just "lambda" λ. It is a constant term added to the equations, which means that it is the same at every event.
λ
His gravitational field equations now read:
|
summed curvature
of spacetime |
+ | λ | = | matter density |
As before, each of these
quantities is really a 4x4 table of numbers. The λ table is constant in
the sense that it is the same at every event in spacetime.
At the time, it seemed like a good idea. But Einstein very soon came to regret the addition, which he saw as harming the beauty and simplicity of the equations.
| Einstein also almost immediately became embroiled in a dispute with the Dutch astronomer, de Sitter. Einstein had hoped that augmenting his gravitational field equations with the cosmological term would preclude empty universes without matter. De Sitter showed that the augmented equations admitted a cosmology with no matter density, contrary to Einstein's expectations. It was an odd spacetime--now called "de Sitter spacetime"--that is everywhere expanding although there is no matter in it. That means that any two tiny test masses that somehow found their way into the universe would accelerate away from each other, whereever they were located. |  |
| De Sitter's spacetime may seem an elaborate
construction. It turns out, however, to be the simplest
spacetime after the flat Minkowski spacetime. It has
constant curvature--that is, it has the same curvature at every
event. To see how simple it is, recall our original recipe for generating curved spaces (not spacetimes). The simplest case was a flat Euclidean surface. We then generated a two dimensional spherical space by looking at the surface of a three dimensional sphere in a three dimensional space; and we generated a three dimensional spherical space by looking at the surface of a four dimensional sphere embedded in a four dimensional space. This procedure in the context of a Minkowski spacetime gives us a de Sitter spacetime. We take a five dimensional Minkowski spacetime (one time dimension, four spatial dimensions). In it, we construct the analog of a sphere. A sphere is the locus of all points that are some fixed distance from a central point. In a Minkowski spacetime, its analog is the locus of all points some fixed spacetime interval from a central point. That locus is the four dimensional hyperboloid shown in the figure. It is a surface of constant curvature, as is a sphere in Euclidean space. The four dimensional surface of that hyperboloid is the de Sitter spacetime. We can then see how the de Sitter spacetime solves Einstein's gravitational field equations augmented with the cosmological term λ. Since de Sitter spacetime has constant curvature, its summed curvature is everywhere the same. So we generate a solution of Einstein's augmented equation merely by picking that de Sitter spacetime whose summed curvature equals the negative of the contant λ term. Then the two terms on the left hand side of Einstein's equation cancel out to zero; the right hand side is also zero since we assume the spacetime is matter free. |
In retrospect, the extra term Einstein added to his equations had a simple interpretation. A uniform mass distribution, if left to itself, ought to collapse under gravitational self-attraction. That is the physical interpretation of the curvature of the space-time sheets that the equations of 1915 were calling for. In adding the cosmological term, Einstein was, in effect, adding a cosmic force of repulsion that would cancel out this natural gravitational self-attraction. That way the matter distribution could remain static.
When de Sitter forms a universe without matter, no gravitational self-attraction of matter opposes λ's powers of repulsion. We can still insert minute test masses into this otherwise empty universe to plumb its properties. With λ's repulsive powers only in effect, we find a universe in which test masses flee everywhere from each other.
| Einstein soon began to have
reservations over his introduction of the cosmological
term. In 1919, he was already calling it: "gravely detrimental to the beauty of the theory." |
This improves on the standard English translation
which says "gravely detrimental to the formal beauty of the theory."
For those who are interested, the original German is "Hierin liegt
ein besonders schwerwiegender Schönheitsfehler der Theorie." Albert Einstein, "Spielen Gravitationsfelder im Aufbau der materiellen Elementarteilchen eine wesentliche Rolle?" Sitzungsberichte der Preussischen Akademie der Wissenschaften, 1919, pp. 349-356. On p. 351. |
In the 1910s, when Einstein proposed his universe, the natural supposition was that the matter of the universe is static on the largest scale. In the 1920s and 1930s, it became clear that this was not so. In fact the matter of the universe is everywhere expanding rapidly and that expansion was adequate to counter temporarily the gravitational self-attraction called for by Einstein's theory. (A good analogy is a stone tossed into the air. Its initial, upward velocity overcomes the downward pull of gravity, but only temporarily.) When these dynamic cosmologies emerged, Einstein renounced the cosmological term, in a joint paper of 1932 with de Sitter.
 |
The relevant passage appears about half way down
the page: "Historically the term containing the "cosmological constant" was introduced in the field equations in order to enable us to account theoretically for the existence of a finite mean density in a static universe. It now appears that in the dynamical case this end can be reached without the introduction of λ." |
Einstein's renunciation of the cosmological term has not proven to be fatal to the idea, however. It gives cosmologists, eager to match their models to the latest astronomical data, an extra parameter to adjust, so that they can get a fit of their model to new, recalcitrant data.
In that context, there is a popular re-interpretation of the cosmological term. To see it, take Einstein's augmented gravitational field equations in the case in which there is no ordinary matter, so the term "matter density" is 0.
|
summed curvature
of spacetime |
+ | λ | = | 0 |
Now just take the λ term and move it to the other side of the equal sign:
|
summed curvature
of spacetime |
= | -λ |
So, where Einstein's original equations used to say "matter density," they now say "-λ." What that means is that Einstein's λ is behaving like an extra sort of matter distributed through space, according to the original equations.
Since we know that λ corresponds to a force of repulsion between matter, it behaves like an odd sort of matter that accelerates the expansion of matter in space. What is odd about it is that all ordinary matter generates attractive gravitational forces. That was the fundamental idea of Newton's original notion of "universal gravitation." As noted above, this now gives some understanding of why the matter-free de Sitter universe is expanding. It is being driven by the repulsions inherent in the cosmological term.
The cosmological constant λ has proven especially useful in recent work in cosmology. Over the last few decades, careful measurements of the motions of distant galaxes have shown motions that do not fit with Einstein's gravitational field equations. Their motion of recession is accelerating faster than Einstein's equations allow. It turns out that we can accommodate those accelerations by adding a cosmological λ term and adjusting its size so that it gives just the observed missing acceleration.

There is an awkwardness in the addition of the term. The great triumph of Einstein's theory had been that it did not need any adjustable parameters to achieve its results. Einstein recovered the anomalous motion of Mercury in 1915 without any tinkering with such a parameter. If the motion of the planet were not anomalous by exactly 43 seconds of arc per century, then his account would have failed.
To make the added term more palatable, the standard approach is to move the λ term to the "matter" side of the gravitational field equations and to declare that it represents a novel form of energy. Since the energy does not radiate light, it is not visible to us. It is called "dark energy."
| To get a sense of the evidential situation, recall the anomalous motion of Mercury. Its perihelion advances by 43 seconds of arc per century. The supposition of extra matter was made as a way of explaining the motion. Leverrier pointed out in 1859 that, if a new planet "Vulcan" were placed in just the right spot, its gravitational pull would explain the anomalous motion. Of course that supposition was not enough. Independent evidence was needed. We had to see the planet. Its position was computed but no telescopic observation ever managed to find it. The supposition of the extra planet Vulcan was abandoned. | This declaration has not solved the problem, yet. All we have is an extra term added to the Einstein gravitational field equations and we can put that term on either "curvature" or "matter" side of the equation. To establish that it really does belong on the matter side, we need some independent evidence that there is an exotic form of matter present. Unfortunatley, no such evidence has been forthcoming. There is, of course, no shortage of speculations and claims that this or that novel account solves the problem. But no consensus account has emerged. Until it does, we should treat the idea that the cosmological λ term represents an exotic form of matter with reservation. That is an awkward outcome since standard estimates suggest that around 70% of the matter in the universe is this "dark energy." |
λ lives on. Einstein would not be pleased.
Copyright John D. Norton. March 2001; January 2007; February 16, October 15, 27, 2008. March 6, 2013, March 4, 2015. October 7, 16, 2020. February 5, 2022.