Special relativity prevails in domains of very high speeds.
General relativity prevails in domains of very strong gravitation.
Relativistic cosmology prevails over enormous distances
| HPS 0410 | Einstein for Everyone |
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Background Reading: J. P. McEvoy, Introducing Quantum Theory. Totem. This book covers very similar ground to this chapter, but in greater detail. Read as much as you like!
Each of the theories we have dealt with so far show us how classical theories break down when we proceed to realms remote from common experience. Classical Newtonian physics fails when we have systems that travel very fast, or we journey into very strong gravity, or we consider cosmic expanses of space.
|
Special relativity prevails in domains of very high speeds. |
|
|
General relativity prevails in domains of very strong gravitation. |
|
|
Relativistic cosmology prevails over enormous distances |
Classical Newtonian physics also breaks down when we consider very small systems, such as individual atoms and the particles from which they are made. Quantum theory gives us our best account of nature in the very small. The standard quantum theory we shall consider here makes no changes to the ideas of space and time of relativity theory. Most standard quantum theories are formulated within spaces and times that conform to Einstein's special theory of relativity or even just to Newton's account. While some versions of quantum theory are set within in the spacetimes of general relativity, a complete adaptation of quantum theory and Einstein's general theory of relativity remains beyond our grasp.
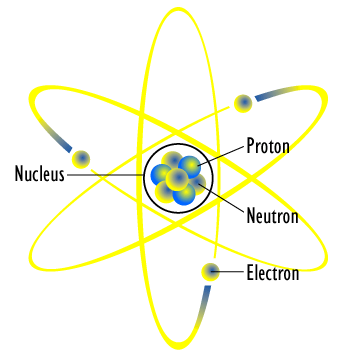

http://en.wikipedia.org/wiki/File:Atom_diagram.png
Quantum theory is a theory of matter; or more precisely it is a theory of the small components that comprise familiar matter. The ordinary matter of tables and chairs, omelettes and elephants is made up of particles, like electrons, protons and neutrons. Quantum theory provides us our best account of these particles. It also provides us with an account of matter in the form of radiation, such as light. It is commonly known that light somehow consists both of light waves and also particle-like photons. The notion of these photons comes from quantum theory (and from Einstein directly, who first introduced them in 1905 as "light quanta").
The central novelty of quantum theory lies in the description of the state of these particles. It turns out that this state does not coincide perfectly with any state we are familiar with from classical physics. In some ways, the particles of quantum theory are like little tiny points of matter, as the name "particle" suggests. In others, they are like little bundles of waves. A full account requires us to see that fundamental particles have properties of both at the same time. There is no easy way to visualize this necessary combination; indeed there may be no fully admissible image at all. The problem of arriving at it remains a challenge today. That problem, however, has proved to be no obstacle to the theory itself. Modern quantum theory has enjoyed enormous empirical success, accounting for a huge array of phenomena and making striking predictions.


Katsushika Hokusai's Great Wave off
Kanagawa: A classic artwork that has passed into the public domain.
| It is possible to describe the basic posits of quantum theory compactly. However these posits are very likely to appear arbitrary and even a little bewildering on first acquaintance. What is needed is some understanding of why those posits were chosen and what problems they are intended to solve. The best way to arrive at this understanding is to review the historical developments in the course of the first quarter of the twentieth century that led to quantum theory. For in that historical development one can see a naturally growing sequence of problems and solutions that eventually issues in the modern theory. | It is interesting to reflect on why
this historical approach is the one now chosen, but it was
not used for the exposition here of special and general relativity.
The reason is that the basic phenomena to which those theories apply
are already somewhat familiar; or it takes very little to introduce
those phenomena. We all can imagine things moving very fast, for
example, and it takes only a little more to imagine that somehow we
cannot accelerated even fast moving things through the speed of
light. Matters are different with quantum theory. The phenomena that control the theory are generally unfamiliar. Those outside physics rarely have a conception of Ehrenfest's "catastrophe in the ultraviolet" for heat radiation; or the odd dependency of the photoelectric effect on frequency; or why the discreteness of the lines of an emission spectrum is classically worrisome. The historical approach familiarizes us with these classically puzzling phenomena. Then, when the resolution emerges as quantum theory, its design and role are immediately apparent. |
Unlike relativity theory, the birth of quantum theory was slow and required many hands. It emerged in the course of the first quarter of the twentieth century with contributions from many physicists, including Einstein.
At the end of the nineteenth century, matter was understood to come in two forms.
| One was particles, localized lumps of stuff that flew about like little bullets. The best investigated of the fundamental particles was the electron. Thomson had found in 1896 that the cathode rays found in cathode ray tubes--the precursor of old fashioned glass TV tubes--were deflected by electric and magnetic fields just as if they were tiny little lumps of electrically charged matter. Atoms, a bound collection of various particles, were also particulate in character. |

http://en.wikipedia.org/wiki/File:Crookes-maltese-tube.jpg
The picture shows a shadow of a Maltese cross produced when cathode rays--apparently moving in straight lines like particles--pass over a Maltese cross shaped barrier in a cathode ray tube.
That light also was just the propagation of little corpuscles was the view bequeathed to physicists by the ultimate authority of the seventeenth and eighteenth century. His celebrated treatise on light of 1704, Opticks, developed an extended account of optical phenomena as resulting from the motion of little light corpuscles. His account coincides largely with what we might now call "ray optics." When allowed to move freely, these corpuscles travel in straight lines. Here, for example, is how Newton described the simple phenomenon of the reflection of images from mirrors.

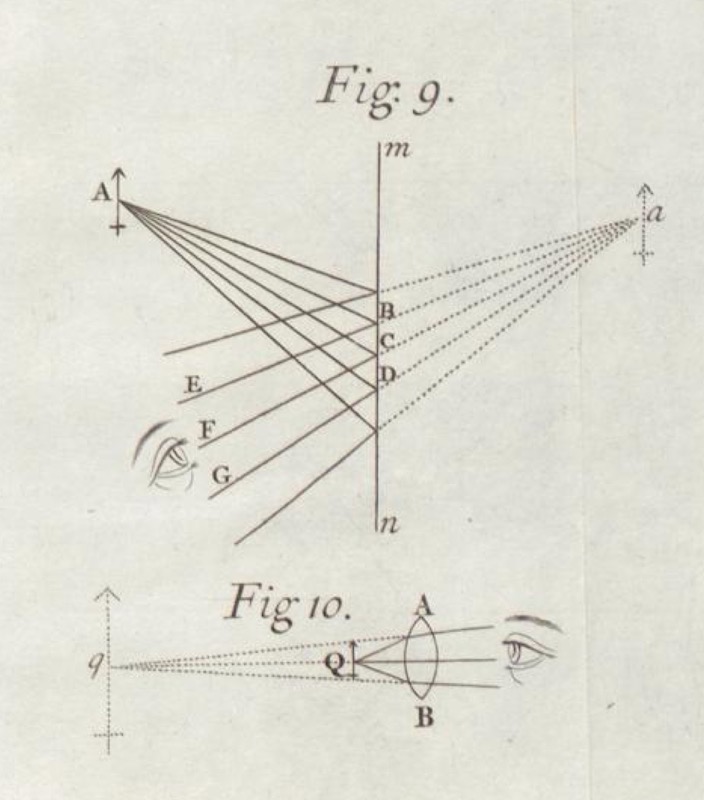

The other form of matter was wavelike matter. Newton's corpuscular picture was challenged in the early nineteenth century by Thomas Young. He argued for a view that had already been explored in Newton's time, that light is a propagating wave. His view eventually won. By the mid and later nineteenth century, that light consisted of propagating waves had become the dominant view. Its most successful expression was in Maxwell's theory. In it, light just consists of electromagnetic waves, that is, wavelike ripples propagating in electric and magnetic fields.
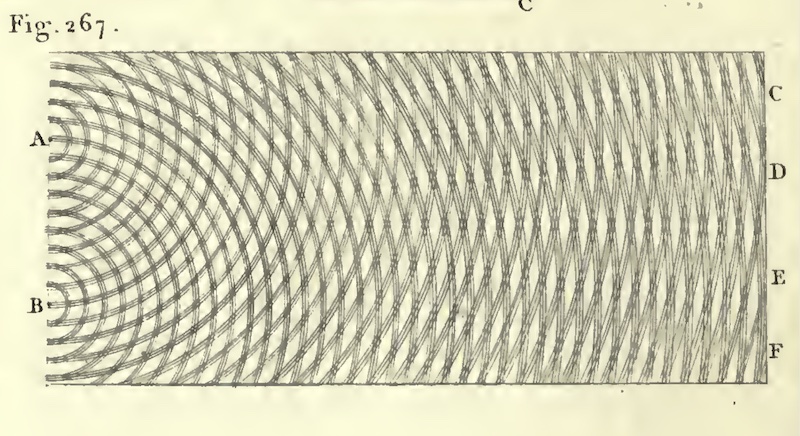
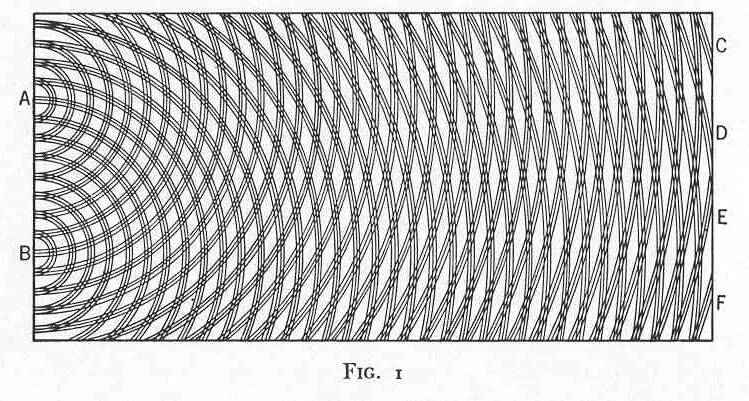
| The most celebrated interference effect arises in the two slit experiment. Waves of light (depicted as parallel wavefronts moving up the screen) strike a barrier with two holes in it. Secondary waves radiate out from the two slits and interfere with each other, forming the characteristic cross hatching pattern of interference. These are the same patterns seen on the surface of a calm pond in the ripples cast off by two pebbles dropped in the water. |
| The essential thing in these interference
experiments is the way the waves combine. The patterns arise because
the waves can add up two ways. In constructive interference, the phases of the waves are such that they add to form a combined wave of greater amplitude. The figure shows the greatest possible effect of constructive interference. All the parts of the two waves line up to interfere constructively everywhere. |
| In destructive interference,
the phases are such that the waves subtract to cancel out. The
figure shows the greatest possible effect of destructive
interference. All parts of the two waves line up in such a way as to
interfere destructively everywhere. In ordinary cases of interference, such as the two slit experiments, both destructive and constructive interference happen in different parts of the region where the waves intersect. That leads to the complicated interference patterns seen. |
Interference effects are readily understandable if one thinks of a wave as some sort of displacement in a medium. A water wave in the ocean, for example, consists of peaks and troughs where the sea water is displaced above and below the mean sealevel. If two waves meet and both peaks coincide, the result is a peak with their combined height. That is constructive interference. If a peak and trough coincide, then the two can cancel out. That is destructive interference.
In the nineteenth century, Maxwell found that that explanation of interference so compelling, that he thought it provided good evidence for an ether. Light, he urged, must be a displacement in something if it is to have peaks and troughs that can cancel out. That something, the carrier of the light wave, is the ether. If light were made up of corpuscles, it seemed impossible that one could combine two corpuscles and have them annihilate.

Manipulated form of http://en.wikipedia.org/wiki/File:Ripple_-_in_rail.jpg
Young reported the decisive interference effects early in the nineteenth century through his two slit experiment, described above. Here is how he portrayed it in his 1807, expansive text book that covered a huge range of topics in what we would now call physics.


With the demise of the ether theory in the early twentieth century, it became clear that something more interesting was at hand. The matter of light itself somehow came in a form that it could locally cancel other light waves. That sort of interaction was an early indication of the sorts of interactions that would become commonplace in quantum theory.
This neat division of matter into particle-like and wave-like would not persist. The story of the coming of quantum theory in the twentieth century is the story of the breakdown of this division. In the sections to come, we shall see how various clues in the observed physical properties of matter showed that this simple division must fail.
| Ordinary matter Gases, liquids, solids |
Radiative matter Light, radio waves, heat radiation |
|
| View at the end of the nineteenth century |
Particles | Waves |
| Clue that this was too simple | Discreteness of atomic spectra (and more) | Thermal properties of heat radiation (and more) |
| View with the completion of quantum theory |
Both wave and particle properties | Both wave and particle properties |

The first clue that radiation might also have particle-like properties came in 1900. It came in apparently innocuous work on heat radiation. This sort of radiation is familiar to everyone. It is the radiation that warms our hands in front of fire, that burns the toast and that provides the intense glare of a furnace. Physicists had been measuring how much energy is found in each of the different frequencies (i.e. colors) that comprise heat radiation. That distribution varies with the temperature of the radiation. As a body that emits radiation passes from red to orange to white heat, the frequencies with the greatest energy change correspondingly.


Public domain image from
http://www.public-domain-image.com/full-image/miscellaneous-public-domain-images-pictures/fire-flames-pictures/fire-close-up-texture.jpg-royalty-free-stock-image.html
| The information about how much energy came in the
various parts of the spectrum of colors could be plotted on a graph.
Here is one of the graphs plotted by Otto Lummer und Ernst
Pringsheim, the leading experimenters from the time. The big peak in
the curve corresponds to the location in the spectrum of most of the
energy of the radiation and thus determines its color. What Lummer and Pringsheim are showing here is that data they have found is not fitted well by the curves of the best current theories. |
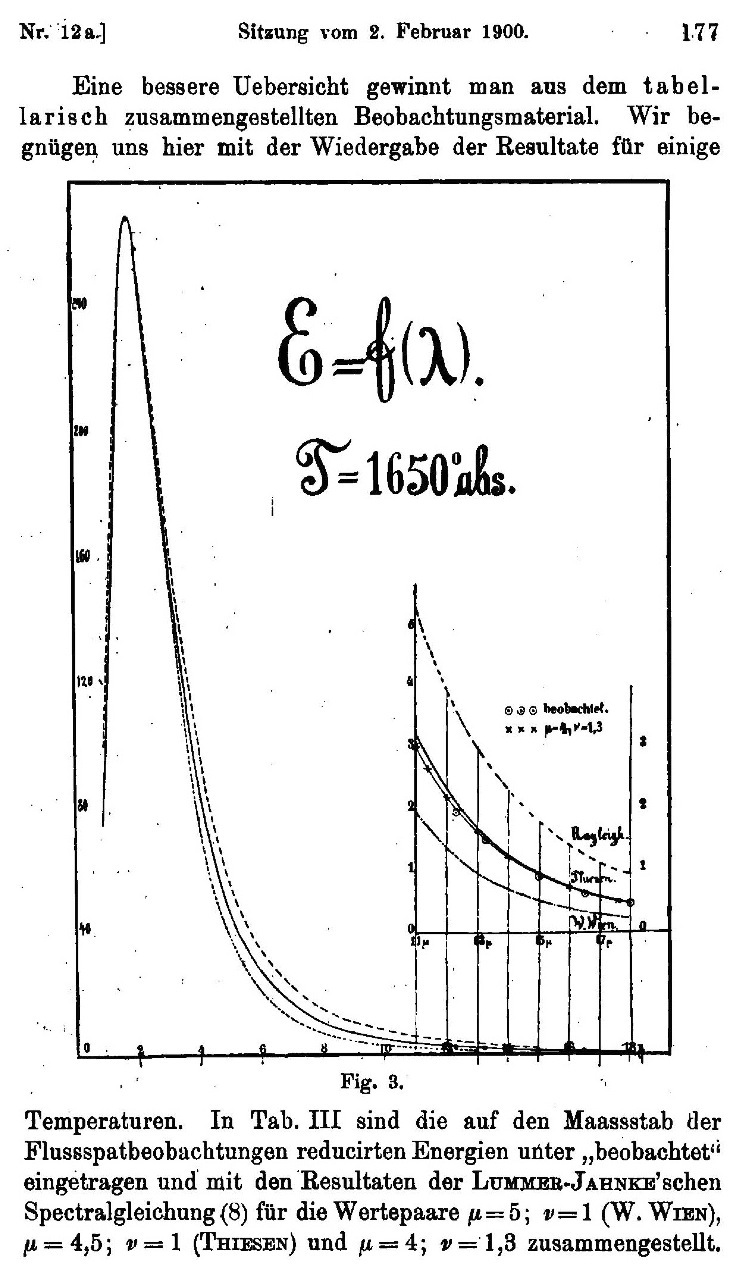 Figure from Otto Lummer und Ernst Pringsheim, "Über die Strahlung des schwarzen Körpers für lange Wellen," Verhandlungen der Deutschen Physikalischen Gesellschaft. 2, (1900) 163-180. |
In 1900, as the newest and latest of the data came in, Max Planck in Berlin was working on understanding the physical processes that led to these distributions of energy. He was well aware of the latest results of his Berlin colleagues, Lummer and Pringsheim, and that no present theory fitted with their latest experimental data. He devised a new account that fitted very well. In his account, heat radiation is a jumble of many frequencies of electromagnetic waves that have come to equilibrium in a cavity. The waves are absorbed and emitted by oscillating charges in the walls of the cavity. That way, the temperature of the walls can be conveyed to the radiation itself. The cavity really just is an oven and it is filling the space inside with heat radiation. This radiation inside the cavity was known as "cavity radiation."

If a tiny window was opened in the walls of the cavity, the radiation released would also have the temperature of the cavity. Some clever thermodynamic arguments showed that it had exactly the same composition as radiation re-emitted by a body at that same temperature if that body had the special property that it absorbed perfectly all radiation that fell on it, before re-radiating it. Such bodies are called "black"; so that form of radiation is known as "black body radiation."
|
Planck found a very simple formula that fitted the latest
experimental results very well. His problem was to tell a
theoretical story about how that formula came about. After some
hesitation, he found such a story. However the essential
computation in his story depended upon a very
odd assumption. (Debate continues today over whether
Planck actually realized how radical this assumption was and how
crucial it was to his account.) Planck modelled the heat radiation
as coming from energized electric resonators. ... |
Deciding what those units were proved to be important. The units of energy were tied to the resonant frequency of the resonator. They were given by Planck's formula:
Energy = h x frequency
That means that the allowed energies are (h x frequency), twice (h x frequency), thrice (h x frequency), and so on.
The letter h stands for a new constant of nature introduced by Planck and now called "Planck's constant." This new constant plays the same of role in quantum theory that the speed of light plays in relativity theory; it tells us when quantum effects will be important. The number is very small, suggesting that quantum effects are to be expected in the small; for example, for ordinary frequencies, units of energy given by Planck's formula will be very small, so we will not notice the granularity it requires when we look at the larger energies of systems ordinary experience. (h = 6.62 x 10-27 erg seconds.)
Planck's original formula applied to the energy of the resonators. He tried hard to confine the discontinuity it suggested to these resonators and even just to the interaction between radiation and the resonators. Over the next decade, other physicists began to see that the discontinuity could not be confined. Computations analogous to those of Planck from 1900 could be applied to heat radiation directly. They drove to the conclusion that Planck's formula applied directly to heat radiation as well. In each frequency, the energy of heat radiation must come in whole units of h x frequency. That conclusion is hard to reconcile with the idea that heat radiation is purely a wave phenomenon.

While Planck may not have recognized how radical his work of 1900 was, Einstein realized that something very odd was afoot with high frequency light and he did it apparently independently of Planck. In 1905 he argued that we needed to change our basic picture of the constitution of radiation.
High frequency light behaves in certain circumstances as
it if were made up of spatially localized bundles
of energy using (once the notation is adjusted) Planck's formula to give
the amount of energy in each bundle. This was a startling reversal. It
seems, at first glance, that we are cast back in time to Newton's old
theory that light consists of a rain of corpuscles.
The energy of each corpuscle, Einstein argued, is equal to h x (frequency
of light).
| The traditional picture inherited from the great achievements of nineteenth century physics was that light is a propagating wave. |
| What Einstein now urged was that high frequency light sometimes behaved as if it were made up of spatially localized bundles of energy. Planck's formula gave the amount of energy in each bundle. So once again light was said to consist of a shower of corpuscles, each corpuscle now with energy equal to h x (frequency of light). |
While this seems like a return to a Newtonian particle view, the return was not and could not be complete. For the wave-based notion of frequency was part of Einstein's hypothesis. And whatever else may come, the experiments on the interference of light remained.
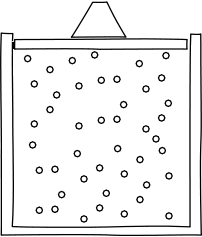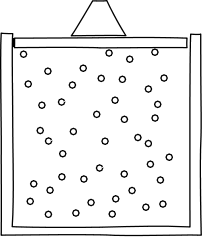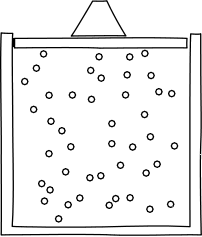 |
Einstein's core argument was ingenious. He looked at the observed properties of high frequency light and noticed they were governed in certain aspects by exactly the same laws that govern ordinary gases. By reverse engineering those gas laws, Einstein could show that they depended essentially on gases consisting of very many spatially localized little lumps of matter, their molecules. He supposed that it was no accident that light and gases obeyed the same laws; they did, he urged, because the light really was made of little localized units--called "quanta"--of energy. |
For a more detailed account of Einstein's core argument,
see the chapter "Atoms and the
Quantum," Section 7, "The
Light Quantum Paper: Einstein's Astonishing Idea."
For a short video of me explaining Einstein's ingenious argument, go to:
"Einstein's Astonishing Idea" on YouTube
or Vimeo

which is a part of the "Instant
HPS" series of short videos

The word "quantum" (plural "quanta") was then just used as a label for a unit of some quantity. In 1905 talk of a light quantum would be understood to be nothing more than talk of a "light unit."
| The best known part of Einstein's 1905 paper on
the light quantum was an observation made towards the end of the
paper. Einstein had been following experiments on the so-called "photoelectric
effect." In it, light is used to kick electrons out of an
electrically charged cathode. According to the wave theory of light,
the intensity of the light ought to determine if the light can
generate these "photoelectrons." For more intense light has more
energy and energy is what is needed to liberate the electrons held
in the cathode's surface. |
It is easy to diminish the intensity of light. We can, for example, just move the light source far away so that the light energy it emits is spread over a great area. The expectation from the wave theory is that this dimmed light will lose its ability to liberate photoelectrons.
Experiment had shown, however, that the intensity did not matter to the ability of light to produce photoelectrons. All that mattered was the frequency of the light. If light was of low frequency, it could not generate photoelectrons, even if the light were very intense. If the light had a high frequency it could produce photoelectrons, even if the light was of very low intensity.
This, Einstein observed triumphantly, is just what one would expect if light energy were localized in quanta with energy given by Planck's formula. All one had to assume was that a single quanta was all that was needed to generate each photoelectron.
| If the light was of low
frequency, its individual quanta would be of low energy, so
no one quanta would be energetic enough to knock electrons out of
the cathode. Increasing the intensity of the light did nothing more
than increasing the number of light quanta showering on the cathode,
all them too weak in energy to liberate a photoelectron. If the light was of high frequency, then each light quantum was individually energetic enough to liberate a single photoelectron. The intensity of the light did not matter. Low intensity meant that there were not many light quanta incident on the cathode. But since only one light quantum is needed to liberate just one photoelectron, the effect would be there for high frequency light, no matter how weak the intensity of the light. |
About fifteen years later in 1921, Einstein won the Nobel prize. His work on the photoelectric effect attracted special mention in the award. The citation read "for his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect."
Einstein's light quantum hypothesis was audacious. It was even beyond audacious.
His other works of 1905 served to complete the physics of
the nineteenth century. Taken together they comprise what is not routinely
called Einstein's
"Annus Mirabilis"
his "miraculous year."
Einstein's doctoral dissertation and his paper on Brownian motion helped establish the reality atoms. That advanced the research of Maxwell, Boltzmann and others from the nineteenth century in statistical physics. They had sought to show that the observable thermal properties of matter could be recovered from statistical analysis of the behavior of very many constituent molecules or other components.
Encoded within the electrodynamics of Maxwell and Lorentz was a new kinematics of space and time. Einstein's work on the special theory of relativity extracted and displayed it.
Einstein's proposal of the light quantum, however, mounted a direct challenge to the major achievement of the Maxwell-Lorentz tradition: the discovery that light was merely a wave propagating in the electromagnetic field.
 |
 |
 |
 |
Did Einstein recognize this distinctive audacity of his light quantum hypothesis?
These sorts of questions are rarely answered easily. However in this case, we have clear evidence that Einstein recognized the audacity of the proposal. In May 1905, Einstein wrote a memorable letter to his friend Conrad Habicht. It assessed the remarkable collection of papers he was writing in 1905.


Conrad Habicht
Einstein's description of the special relativity paper is reserved. He merely says that the kinematic part of the paper "will surely interest you." However the light quantum paper, he assures Habicht, is "very revolutionary." No other of the papers of 1905 mentioned in the letter is described this way.
The letter is so striking that it is worth seeing in full. Here is a facsimile of the first page.


https://commons.wikimedia.org/wiki/File:Die_Echte_Rotzunge_oder_Limande...IMG_2717ВЕ.jpg
The text reads in translation:
Bern,
Thursday [18 or 25 May 1905]
Dear Habicht,
Such a solemn air of silence has descended between us that I almost feel
as if I am committing a sacrilege when I break it now with some
inconsequential babble. But is this not always the fate of the exalted
ones of this world?
So, what are you up to, you frozen whale, you smoked, dried, canned
piece of soul, [German, Seele = soul, not
sole (fish)] or whatever else I would like to hurl at your
head, filled as I am with 70% anger and 30% pity! You have only the
latter 30% to thank for my not having sent you a can full of minced
onions and garlic after you so cravenly did not show up on Easter. But
why have you still not sent me your dissertation? Don't you know that I
am one of the 1 1/2 fellows who would read it with interest and
pleasure, you wretched man? I promise you four papers in return,
the first of which I might send you soon, since I will soon get the
complimentary reprints. The paper deals with radiation and the energy
properties of light and is very revolutionary, as you will see if you
send me your work first.
The second paper is a determination of the true sizes of atoms from the
diffusion and the viscosity of dilute solutions of neutral substances.
The third proves that, on the assumption of the molecular theory of
heat, bodies on the order of magnitude 1/1000 mm, suspended in liquids,
must already perform an observable random motion that is produced by
thermal motion; in fact, physiologists have observed (unexplained)
motions of suspended small, inanimate, bodies, which motions they
designate as "Brownian molecular motion."
The fourth paper is only a rough draft at this point, and is an
electrodynamics of moving bodies which employs a modification of the
theory of space and time; the purely kinematic part of this paper will
surely interest you.
Solo gives private lessons the same as before, and cannot bring himself
to sit for the exam; I feel very sorry for him, for he leads a sad
existence. He also looks quite exhausted. But I don't think it's
possible to steer him to more bearable living conditions-you know how he
is!
Greetings from your A.E.
My wife and the dickey bird, who is now 1 year old, send you their best
regards. Send me your paper soon!
Translation from Einstein Papers,
Vol. 5, Doc. 27.
If this corpuscular view of light is so successful, do we need the wave view at all? In 1909, Einstein showed that the properties of heat radiation could only be successfully explained if we used both the wave and particle view.
To arrive at this conclusion, he considered thermal fluctuations. They arise in any thermal system, where the thermal system consists of very many component systems that have come to some sort of equilibrium:
• If we think of an ordinary body surrounded by air, there are slight fluctuations in the pressure of the air when more and less molecules collide with the body at any moment.
• If we think of a body surrounded by a complicated system of waves, there is a similar effect. We might imagine a boat tossed on stormy seas. One wave after another crashes into the boat and tosses it about. The effect varies over time.


https://commons.wikimedia.org/wiki/File:VilhelmBille_boats_at_sea.jpeg
Einstein imagined a mirror within a bath of heat radiation. If the heat radiation consists of corpuscle-like quanta, then fluctuations would arise in the motion of the mirror from the impact of the light quanta, analogously to the fluctuations dues to gas molecule collisions. If the heat radiation consists of waves, then irregularities in the waves would also lead to fluctuations in the motion of the mirror, analogous to the tossing of a boat on stormy seas. Which would be the case for heat radiation?
Einstein was able to use general arguments in the statistical mechanics of thermal systems to determine the magnitude of the fluctuations in the motion of the mirror. He recovered a striking result: the full observed effect came from the sum of two terms, one a particle term, the other a wave term. Both wave and particle fluctuation processes were present.
| fluctuations in heat radiation | = | term dues to the wavelike character of heat radiation | + | term due to the particle like character of heat radiation |
The need for both is sometimes called "wave-particle duality." Something like this is needed, for, whatever else our accounts of light must do, they still must accommodate Thomas Young's observations from the early 19th century of interference phenomena in light.
Many of you will want to use the word "photon" interchangeably with Einstein's "light quantum." There is probably not much harm in doing that as long as you realize that the word "photon" comes from a later era in quantum theory. It was introduced by G. N. Lewis in 1926, 21 eventful years later.
When we use the word photon, the natural presumption is that we are referring to the entity that derives from the completed quantum theory of the 1920s and 1930s. When Einstein proposed his light quanta, not even an Einstein could anticipate quite how radically the emerging quantum theory would diverge from classical ideas. Einstein's proposal of 1905 was quite restricted; he posited that the energy of high frequency light was spatially localized into the little lumps he called light quanta. He could not then know how things would transpire for low frequency light. And his proposal of 1905 did not say anything about the momentum of the light quanta. That light quanta also carry momentum was inferred later.

The analysis of heat radiation and the power of light to generate photoelectrons provided the first clues that this wavelike form of matter was not merely wavelike, but also had particle-like aspects as well. What of the particles that make up matter? What of the electrons that Thomson had found in 1896? The clue that they also had wavelike aspects eventually derived from observations in atomic spectra.
If gases are energized by heating or passing an electric discharge through them, they emit light. The orange sodium vapor lamps or bright white mercury vapor lamps used in parking lots employ this mechanism in its simplest form. The reverse process also occurs. Gases will absorb light--that is how they can block transmission of light.

http://en.wikipedia.org/wiki/File:Gase-in-Entladungsroehren.jpg

http://en.wikipedia.org/wiki/File:Edelgase_in_Entladungsroehren.jpg
One might expect that such emissions (and absorptions) contain all frequencies (colors)--a perfect rainbow--even if the intensity of light across the spectrum might vary. They do not. Gases are very selective in the frequencies they emit and absorb. They will emit and absorb only a few very particular frequencies. The frequencies emitted form what is called the atomic emission spectrum of the element; and those absorbed form the absorption spectrum. The frequencies in them are distinctive: they can be used as a characteristic signature for identifying an otherwise unknown gas.
| Here is the emission spectrum of hydrogen gas. The light emitted by excited hydrogen has been spread out into its component frequencies by passing it through a prism or diffraction grating. The light then darkens a photographic emulsion in different places according to its frequency.The series of lines shown is the so-called "Balmer series" that appears in the visible and near visible frequencies of light. (Wavelengths are shown in units of Angstroms.) Image from Gerhard Herzberg, Atomic Spectra and Atomic Structure. Prentice-Hall, 1937. | 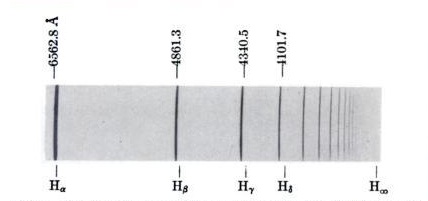 |
In 1913, Niels Bohr reported on his efforts to devise a model of the process of light emission from the atoms of elements that would explain the very particular frequencies emitted. The problem proved to be far harder than one would expect. Then, the best model of an atom was Rutherford's nuclear model. According to it, an atom is like a little solar system. It has a massive, but tiny, positively charged nucleus. That nucleus exerts an attractive force on lighter negatively charged electrons that orbit it, rather like the way the planets orbit the very massive sun.
| In the Rutherford model, exciting a gas by
passing high voltage electricity through it would energize the
electrons, which could then move farther away from the attractive
pull of the nucleus. When they fell back towards the nucleus, the
energy they gained would be lost as light energy; that emitted light
forms the emission spectrum. The first difficulty was that, as they fell back to the nucleus, they would pass through a continuous range of orbital frequencies and thus emit a continuous range of frequencies of light. There was no way to limit the emitted light to just a few special frequencies. The second difficulty was more serious. Nothing stops the emission of energy by the electrons through this process of light emission. They would continue to do it until they crashed into the nucleus. According to classical electrodynamics, this would happen very quickly. It was not clear that Rutherford's model allowed matter made of atoms to exist at all. |
| Bohr solved both
problems with a proposal of breath-taking audacity. Classical
electrodynamics was quite clear: an electron orbiting the nucleus is
accelerating and therefore must radiate energy. It would be like a
little radio transmitter, broadcasting electromagnetic waves. In the
process, it must lose energy, fall deeper into the attractive pull
of the nucleus and eventually crash into it nucleus. Bohr simply posited that this was not true. Rather, he asserted that there are stable orbits arrayed around the nucleus in which an electron could orbit indefinitely without losing any energy. |
| Next, Bohr supposed that electrons can jump up
and down between these allowed orbits. If an electron
is to jump up, away from the nucleus to a higher energy
orbit, it needs to gain energy. That enables it overcome the pull of
the atom's positively charged nucleus and climb away from it. The
electron gets that extra energy from light falling on the atom. The
energy of the light is transferred to the electron, which can then
jump up to a higher energy orbit. The incident light must deliver
exactly the right amount of energy to make up the difference between
the energy of the orbit left behind and the one to which the
electron jumps. In addition Bohr assumed that the amount of energy drawn from the exciting light conforms with Planck's formula: the energy is just h times its frequency. The outcome is that light only of a very specific frequency can excite the jumps between two specific orbits. For some specified jump, the frequency of the light has to be tuned precisely so that h times the frequency exactly matches the energy needed to complete the jump. |
| Bohr's theory also allows for the reverse
process. Once an electron has jumped up to a higher energy orbit, it
will not stay there. It will jump back down
to a lower energy orbit. In the process, it will re-emit the energy
it gained in jumping up in the form of light of a definite
frequency. Once again, the energy of the light emitted will conform
to Planck's formula and be equal to h times its frequency. As a result, when an electron jumps down between two orbits, it emits light of a definite frequency that is characteristic of exactly that jump. |
Eventually, these quantities of light energy that the atom
absorbs and emits came to be identified with
Einstein's light quanta. In 1913, however, Bohr was cautious. He
did not say that a light quantum is emitted. He simply spoke of
"the emission of a homogeneous radiation, for which the relation
between the frequency and the amount of energy emitted is the one given by
Planck's theory."
This avoidance of Einstein's quantum was no accident. Bohr was a fierce
opponent of Einstein's notion and only relented in his opposition
when new developments in the 1920s compelled the acceptance of Einstein's
notion.
Having made those assumptions, Bohr could read off the oddest result from the observed atomic spectra. Since only very few frequencies of light were present, it followed that only very few jumps were possible, so that only very few orbits were permitted for the electron. It was as though our sun allowed a planet to orbit where Venus is and where the Earth is; but it prohibited any planet in between.
All that remained was to figure out just which of the many possible orbits are found in this favored set of stable orbits. That was relatively easy to do. The observed spectra gave a complete catalog of the energy differences between these allowed, stable orbits. Each line in the observed spectra resulted from electrons jumping between two specific orbits. It is a numerical exercise to determine precisely which those few orbits are. The calculation was not so different from this exercise in geography. If we are given the distances between every pair of cities in a country, we can use those data to figure out where on the map each city is found. Atomic spectra gave Bohr the energetic distances between his allowed orbits. From those data he could determine the energies and thus locations of those allowed orbits.
| When Bohr did that, he found a very simple way to summarize just which of the orbits were allowed. They were those whose orbital angular momentum came in units h/2π. Just as Planck's relation told us that radiant energy comes in whole units of h x frequency, Bohr now found that orbiting electrons always must have whole units of angular momentum: one h/2π, two h/2π, three h/2π and nothing in between. | We have seen that the ordinary (linear) momentum of a body is just its mass times its velocity. Angular momentum is an analogous quantity that plays an important role in the dynamics of rotating or orbiting systems. For a small mass like a classical electron orbiting a nucleus, it is defined as the electron's mass x radius of orbit x angular speed of electron. |
Angular
momentum
= one h/2π, two h/2π, three h/2π, . . .
Bohr's theory was puzzling, even maddening. Just as with Einstein's hypothesis of the light quantum, it seemed to require that classical physical notions both hold and fail at the same time. That was not a comfortable situation. Those discomforts were eclipsed by a brighter fact. Bohr's theory worked, and it worked very well. Observational spectroscopy was providing theorists with an expansive catalog of spectra of many substances under many different conditions. Starting from Bohr's theory, physicists were able to develop an increasingly rich and successful account of them. While it was clear that something was not right, in the face of these successes, it was tempting to postpone asking too pointedly how this goose could keep laying golden eggs.
| The central result of Bohr's theory of 1913 was that the angular momentum of orbiting electrons came in full multiples -- quanta -- of h/2π. In the years immediately following, that simple condition was expanded into a broader condition that a quantity known as "action" came only in whole multiples for physical systems that returned periodically to the same initial condition. As a result the term "quantum of action" entered the physicists' vocabulary. | This sidebar should contain a brief sentence that gives you a useful idea of the physical quantity "action." Alas, I've been unable to figure out what that sentence might be. It probably doesn't help too much if I tell you that the trajectories of bodies obeying classical physical laws can be picked out as those that render extremal the action added up along the trajectories. Did that help? I didn't think it would. |

Bohr's theory of 1913 and its later elaboration gave a wonderfully rich repertoire of methods for accounting for atomic spectra. They depended on a contradictory mix of classical and non-classical notions. By the early 1920s, the limits of this system began to show and theorists also turned to the task of making some coherent sense of this body of theory that soon came to known as "the old quantum theory."
The major breakthroughs to the "new quantum theory" came in the middle of the 1920s. A number of different theorists found ways of developing coherent theories of the quantum domain; and they all eventually proved to be different versions of the same new theory. Heisenberg, Born and Jordan first developed matrix mechanics. Its basic quantities were infinite tables of numbers -- matrices -- drawn as directly as possible from observed quantities like atomic spectra.
Another approach proved equivalent and is easier to picture. It was based on a supposition by de Broglie of 1923 and developed by Schroedinger in 1926. Einstein had shown that a wave phenomenon, light, also had particle like properties. Might the reverse be true also? Might particle like electrons also have wave properties?
The hypothesis answered yes. It associated a wave of a
particular wavelength with a particle of some definite momentum.
Here is de Broglie's formula that tells us which wavelength goes with
which momentum:
momentum = h / wavelength
Notice how similar it is to Planck's formula which relates energy and frequency. Here is Planck's formula again:
energy = h x frequency
The two together form the foundation of the matter
wave approach. They tell us how to assign a wave of some definite
frequency and wavelength to a particle of some given energy and momentum.
Here's a way to see the two
equations in even more similar form. For a periodic process we can write
frequency = 1/period, where "period" is the time needed for the process to
recur. Then Planck's formula becomes
energy = h / period.
Now the equations relate momentum to a length (the wavelength) and energy
to a time (the period).
The beauty of the matter wave hypothesis is that it explained
naturally why only very particular energy states are admissible
for electrons bound in atoms. The reason that only few energy states are
admissible for these electrons derives directly from the fundamental
differences between particles and waves. We can see these differences by
considering a very simple case, a particle/wave trapped in a box.
To keep things as simple as possible, we will imagine that the particle
can only move in one spatial dimension; it
finds itself in a one-dimensional box.
| To begin, imagine an ordinary, classical particle confined to a box. It bounces back and forth between the walls. Classical physics allows it to move at any speed. As a result it can have a continuous range of different energies. |
| Now imagine instead that we are confining a wave
to the same box. The stable waves that can persist within the box
are so called "standing waves." Anyone who plays a stringed instrument is familiar with them. When a string is plucked or bowed, the base note results from a standing wave whose half-wavelength is the length of the string. There are overtones also formed that give the richness of the sound. These are smaller standing waves, whose wavelengths equal the length of the string, 2/3 that length, half that length, and so on. The essential condition is that a wave can form as long as it has nodes--the points of no displacement--at either end of the string. The matter waves that can form within the box have the same structure as these tones and overtones. They have wavelengths of once, 1/2, 1/3, ... , times the double width of the box. (We use the double width since standing waves have nodes at each half wavelength.) Each of these waves turns out to have a different energy that depends on the wavelength of the standing wave. Thus only very few definite energies are permitted for the waves trapped in the box; the many intermediate energies between them are not allowed. |

https://commons.wikimedia.org/wiki/File:Bowed_violin_string_in_slow_motion.gif
This file is licensed under the Creative Commons Attribution 3.0
Unported license.
What of de
Broglie's relation, momentum = h/wavelength? Are we to say that
the standing waves in the box have momenta proportional to h/2, h, (3/2)h,
2h, ... etc. corresponding to the above allowed wavelengths. Well--almost.
The standing wave with wavelength equal to the width of box could be
associated with a particle moving to the right with momentum = h/(width of
box) and one moving to the left with momentum h/(width of box). But a
standing wave is propagating neither to the right nor to the left.
To get the wave to stand still, we form the superposition of these two
waves. Superposition allows us to have a wave that is moving both to the
left and right at the same time, and thus goes nowhere. The animation
shows two waves propagating in opposite directions. They are
superposed--"added up"--to form a standing wave.
See the next chapter for more on superposition.
The situation for an electron in a hydrogen atom is essentially the same. The electric attraction of the positively charged nucleus forms a prison that traps the electron, just as the box above traps the wave. The wave in the box may persist only in a few energy states. Correspondingly an electron-wave trapped in a hydrogen atom may persist only in a few definite energy states. These turn out to the be the energies of the stable orbits of Bohr's theory.
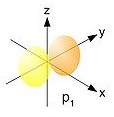


http://commons.wikimedia.org/wiki/File:Single_electron_orbitals_s.jpg
http://commons.wikimedia.org/wiki/File:Single_electron_orbitals_p1.jpg
http://commons.wikimedia.org/wiki/File:Single_electron_orbitals_d.jpg
http://commons.wikimedia.org/wiki/File:Single_electron_orbitals_f.jpg
While those energies survive, what does not survive from Bohr's theory is the idea of the electron as a spatially localized particle orbiting the nucleus in a classical circular or elliptical orbit, but nonetheless violating classical electrodynamics by not radiating. The space around the atom's nucleus is filled with a standing wave of the electron. Classical electrodynamic theory no longer directly applies; the earlier contradiction with that theory has evaporated.
In the later part of the 1920s, all these ideas coalesced
into what was called the "new quantum theory," to distinguish it
from the "old quantum theory" of the decades before. There were
• matrix based approaches proposed by Heisenberg, Born and Jordan; and
• the matter waves of de Broglie and Schoedinger; and
• Dirac's classical "c-numbers" and quantum "q-numbers."
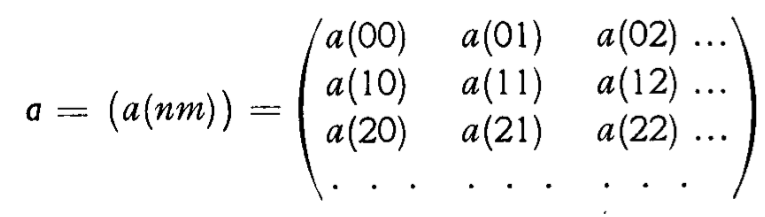
A matrix from Born and Jordan's paper on the
new quantum mechanics of 1925.
It soon became clear that all these approaches were really just the same theory dressed up in different mathematical clothing. The puzzling properties of light and matter that led to this theory were now essentially resolved. The solution lay in a new conception of the nature of matter. Matter fundamentally is not made of particle OR waves; it consists of a form of matter that, roughly speaking, is both particle AND wave; and this is true both for ordinary matter like protons and electrons, and for radiative matter like light.
This new synthesis, however, left a legacy of enduring problems.
| First, the new theory introduced an element of probability that was unknown in classical physics. There are many processes for whose outcomes the theory can only give probabilities. Will this radioactive atom decay now or later? The best the theory can offer are probabilities. This circumstance proved deeply troubling to many thinkers of the era, including Einstein. They found it repugnant to think that the fundamental laws of the universe might be probabilistic and described the difficulty as a breakdown of "causality." There were deeper problems. |
| Second, the new quantum theory worked very well for small particles. However it was far less clear how it should be applied to macroscopic bodies. Tables, chairs, houses and elephants do not obviously manifest a combination of wave and particle-like properties. Yet the theory said that they must. We will see in the next chapter how that problem continues to vex us today. |  |
Copyright John D. Norton. April 2001; March 16, August 22, November 23, 2008; April 7, 2010; April 6, 2013, April 6, 2015; April 10, 14, 2017. November 19, 2018. November 9, 2020. February 6, March 6, April 11, 2022. November 15, 2023. April 4, 2024