| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Linked document:
Euclid's Postulates
and Some Non-Euclidean Alternatives
So far, we have examined the geometry of homogeneous spaces. That is, we have been examining spaces that are everywhere the same, geometrically. This means that if a space is flat in one place, we have assumed it is flat everywhere. Or if it has positive curvature in one place, we have assumed it has the same positive curvature everywhere else.
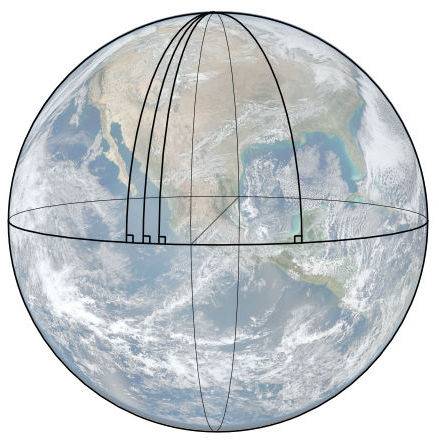
| A simple example is just the surface of a sphere. Its intrinsic geometry has positive curvature and that curvature is the same everywhere. This means that the geometry of each little patch of the sphere's surface is same as every other little patch. |  |
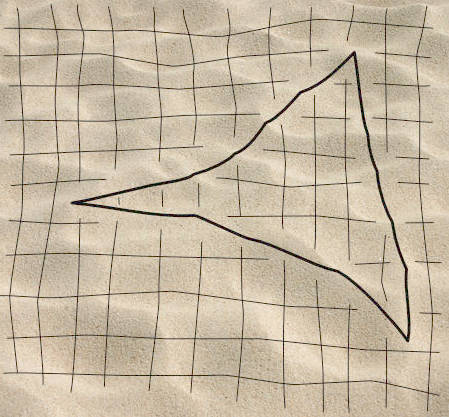 |
Nothing makes us to restrict ourselves to surfaces like the surface of a sphere. We can investigate surfaces that have curvatures that vary from place to place: no curvature here; positive curvature there; even more positive curvature somewhere else; and negative curvature in yet another place. A surface with that sort of geometry is not hard to visualize. It is just a dimpled surface shown here, with flat parts, dome-like parts with positive curvature and saddle-like parts with negative curvature. |
If we have a space of variable curvature, how do we determine the curvature at each place? Since the curvature varies from place to place, the methods that we learned in the last chapter will be of limited use. We could draw very big triangles to check how the sums of their angles differ from 180o. But if the curvature of the space varies a great deal over the region of space covered by the triangle, that sum will not tell us much of any use.
We will need a means that works locally, that is, it works in tiny little patches of the space. We will develop these means below, first for the familiar case of spaces of constant curvature.
If we are in a curved space, here is a convenient way to determine the curvature without having to resort to a higher dimensioned embedding space. We start with a straight (geodesic) line and erect straight (geodesic) perpendiculars on it. We then proceed along the perpendiculars, noticing whether they converge or diverge (or neither). That tells us immediately what sort of space we are in. There are three cases corresponding to the three geometries.
| In the Euclidean case, the perpendiculars neither converge nor diverge. |
| In the case of a spherical geometry of positive curvature, the perpendiculars converge. |
| In the case of a hyperbolic geometry of negative curvature, the perpendiculars diverge. |
| So far, we have just considered the simplest case of geodesic deviation. In that simplest case, we started out with a family of geodesic curves perpendicular to some base line and checked whether they converged or diverged. We can still use geodesic deviation if we start out with a family of geodesic curves that are not perpendicular to some baseline. All we check for is whether they converge or diverge faster or slower than a straight line projection would indicate. | Just how much convergence or divergence should we expect with a "straight line projection"? Under it, the distances by which the geodesics approach or recede are just directly proportional to the distance we move along the geodesics. If they are converging, when we go twice as far, for example, then the geodesics near each other converge exactly twice as much. |
| Here's how things work out for the case of positive curvature. We start out with a family of geodesic curves that are initially diverging. The dotted lines show how they would continue to diverge under straight line expectations. What they actually do is to diverge slower than these expectation. So we have a case of positive curvature. |
| Now here's the other case of positive
curvature. The family of geodesic curves are initially converging.
The dotted lines show how they would continue to converge under
straight line expectations. What they actually do is to converge
faster than these expectations. So we have a case of
positive curvature again. Note that in both cases of positive curvature, the deviation from linear expectations is inwards. |
All this is reversed for the case of negative curvature. Deviations from the linear trend are always outwards.
The notion of geodesic deviation enables us to distinguish two types of curvature in geometry.
The first is most familiar to us, extrinsic curvature. It arises whenever we have a surface that curves into a higher dimension. We have seen many examples. One of the simplest arises when a flat sheet of paper is bent or rolled up into a cylinder. A more interesting case arises when the surface is dome-like, such as a hemisphere.
In this last case of the hemisphere, the curvature of the surface into the higher dimension is associated with a failure of ordinary Euclidean geometry in the surface of the sphere. This failure of Euclidean geometry arises fully within the surface; it is a manifestation of intrinsic curvature. To summarize:
| A surface exhibits extrinsic curvature when that surface curves into a higher dimension in an embedding space. | A surface exhibits intrinsic curvature when the geometry within the surface differs from flat, Euclidean geometry. It is revealed by geodesic deviation. |
You might think that extrinsic curvature and intrinsic curvature must go hand in hand; whenever you have one, you have the other. That is not so. It is easy to have a surface that has extrinisic curvature, but no intrinsic curvature. The example is a familiar one.
| Take a flat Euclidean surface. The geometry on its surface will be Euclidean, obviously. That means, if we draw a triangle on the surface, its angles will sum to 180 degrees. |
| Now roll that surface up into a
cylinder. That means the surface has now acquired extrinsic
curvature. However its intrinsic curvature has not changed; it is
still intrinsically flat. To see this consider any figure that you
might have drawn on the surface. Within the surface, nothing
about the figure is disturbed. If the figure conformed to
Euclidean geometry before being rolled up, it will conform to
Euclidean geometry after being rolled up. For example, when the surface was rolled up, the sides of the triangle shown are bent into the higher dimension by the rolling up of the surface. But within the surface, they remain straight lines in the sense relevant to the intrinsic geometry. That is, they remain geodesics, the shortest distances in the surface between the corners of the triangle. Correspondingly, by measures taken within the surface, the angles of the triangle will still sum to 180 degrees. |
| One of the special benefits of geodesic deviation is that it works in surfaces whose curvature varies from place to place. It is the local measure of curvature we need. We may have a surface with positive curvature, but the amount of curvature varies from place to place. The rate of convergence will tell us how much curvature we have at each place. It will also tell us if the curvature varies to zero (flat) or becomes negative. Here is a surface whose curvature varies from place to place. Geodesic deviation allows us to track how the curvature changes. | When we looked at spaces of constant curvature, we defined geodesics as curves of shortest distance between two points. That definition remains when we move to spaces of variable curvature. Geodesics are still the curves of shortest length. In familiar terms, imagine that you are hiking over a rocky terrain whose surface has a curvature that varies from place to place. If you walk along the shortest route you can find, you have just traced out a geodesic of that surface. |
| To begin, on the left, there is no divergence or convergence of the perpendicular geodesics. The geometry within the surface at the leftmost part is flat. | How can that be? The surface is curved into a cylinder! That only means that the surface has extrinsic curvature. It is bent into a higher dimension. There is no intrinsic curvature; that is, there is none that manifests geometrically within the surface. |
In the central part, the surface adopts the negative curvature of a saddle shape. The perpendiculars there diverge outwards from the central part of the saddle.
On the right, the surface is positively curved. So there the perpendiculars converge as we move away from the central portion of the curved surface.
So far we have seen that the curvature of a surface can vary from place to place. It might be zero here, positive there and negative over there. However, at any one place in the surface, there has only been one curvature. That turns out to be a special case that arises in the simple example of a two dimensional surface.
When we consider spaces of three or more dimensions, the sort of curvature we have can vary according to the direction in which we are looking. More precisely, we can slice up a three or higher dimensional space into two dimensional sheets with different orientations. In making the sheets, we make them as straight as we can; that is, we make sure that they are built from straight lines running in two directions. As before, we use geodesic deviation to determine the curvature intrinsic to each sheet. In general, we will find that different two dimensional sheets going through the same point in the space will have different curvatures.
| Let us start with a simple example in which there is no difference in curvature according to the direction considered. Here's a three dimensional Euclidean space sliced into sheets that run front-back and left-right. (As required above, these sheets are built from straight lines that run front-back and east-west, so they are as flat as we can make them.) We use geodesic deviation to find the curvature in the sheet at some point P. There is none; the sheet is flat. |
| We might slice up the very same space into sheets that run front-back and up-down. We can use geodesic deviation again to find the curvature at the same point P, but in this new sheet. There is none; the sheet is flat. |
| A convenient way of generating a space like this is by extruding a shape from a lower dimension. In this case, we can extrude a square into a third dimension to create the shape. |
Things worked out simply in this last example. But it is entirely possible that they do not and that we end up with a different curvature from that found at point P in a sheet that runs in a different direction. You are probably wondering how this can come about. The next section constructs a three dimensional space that has different curvatures in different sheets.
The construction of this section is a little taxing until you are used to visualizing curved spaces of various dimensions. So work through it if you can. Or, if you prefer, just accept that in three and higher dimensions, the curvature of space can vary accoring to the direction of the sheet considered.
To begin, recall that we can always add an extra dimension to a space by "extruding" it, that is, stacking up repeated copies in a new direction. That adds to the space we started with. For example, start with an ordinary, flat two dimensional surface that runs front-back and left-right, such as the square shown above. Extrude it in the obvious way in the up-down direction and we have constructed an ordinary, flat, three dimensional space.
| We need not start with an ordinary
flat surface. We might start with a one dimensional circle that runs
left-right and extrude it up-down. That
is, we start with a line, the circumference of the circle. It is
just a one-dimensional space. It is extruded in a direction
perpendicular to the circle. What results is a two dimensional
surface. It is the surface of a cylinder. So far nothing unusual has happened as far as curvature is concerned. The intrinsic curvature of the surface of the cylinder is flat, that is, Euclidean. We already saw this above. Just imagine that the cylinder is slit vertically and unrolled. We end up with a flat sheet on which the geometry is Euclidean. In unrolling it, we haven't changed any of the geometry intrinsic to the surface. |
| Now let us do something a little
fancier. We start with a two dimensional space that is the surface
of a sphere. In that surface, we have two directions: east-west and
north-south. We form a three dimensional space by extruding
the sphere in a third up-down direction. The construction is the same as the construction of the cylinder above. All that has changed is that the one-dimensional line of the circumference of the circle has been replaced by the two dimensional surface of a sphere. The picture shows roughly what the resulting space would be like. It is only a rough picture since the extruded space has a geometry that makes it impossible to draw faithfully on a two dimensional Euclidean page. The figure is trying to show a three dimensional, non-Euclidean space that consists of the surfaces of many spheres all stacked up on top of each other in an additional dimension. |
| At any point in this space we can take different slices. For example, we can take an east-west north-south slice. The resulting sheet is just the original two dimensional sphere. Geodesic deviation will tell us that the sheet has positive curvature. |
| We could also slice the space in the east-west
up-down direction. That defines a sheet that might coincide
with the east-west equator of the sphere and what that equator
extrudes into in the up-down direction. That is just a cylinder. We
can use geodesic deviation to determine the curvature in this sheet.
Since the cylinder is just a flat surface rolled up, we will find
zero curvature. Summarizing: in this space, if we form a sheet by slicing in one direction, we end up with a sheet that has positive curvature. If we form a sheet by slicing in a different direction at the same point, we end up with a sheet that has zero curvature. |
These last two sections show just how complicated curvature can be in geometry. Curvature can vary from place to place in a space; and at one place it can vary according to the direction considered. That capacity for complexity is going to prove very useful. It turns out to be just what Einstein needed to represent gravity geometrically. But now we are getting ahead of ourselves; that will be our topic in the next chapter.
Copyright John D. Norton. February 14,
September 22, October 13, 2008; March 1, 2010. February 15, 2017.
Redrawn figure November 20, 2019. September 29, 2020. January 31, 2022.