| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
In the last chapter, we explored the geometry induced by the postulate 5NONE by means of the traditional construction techniques of geometry familiar to Euclid. We drew lines and found points only as allowed by the various postulates. The outcome was a laborious construction of circles and triangles with some quite peculiar properties. We constructed a circle with center O and circumference G, G', G'', G'''.
Its circumference is only 4 times is radius (and not the 2π times its radius dictated by Euclid's geometry). Its cirumference is both a circle and a straight line at the same time. Each of its quadrants are triangles with odd properties. The triangle OGG', for example, has three angles, each of one right angle. So the sum of its angles is three right angles (and not the two right angles dictated by Euclid's geometry).
You would be forgiven for thinking that the new geometry of 5NONE is a very peculiar and unfamiliar geometry and that there is no easy way to comprehend it as a whole. The surprising thing is that this is not so. The geometry of 5NONE and the geometry of the other postulate 5MORE turn out to be the geometries that arise naturally in surfaces of constant curvature. Recognizing that fact makes it easy to visualize these new geometries and one rapidly develops a sense of the sorts of results that will be demonstrable in them.
We will see in this chapter how this arises. It is a trick that makes visualizing the geometries of 5NONE and 5MORE easy. Indeed, it makes makes it too easy. We now risk a new danger: we may just overlook the fact that we are really dealing with new and different geometries.
The geometry of 5NONE proves to be very familiar; it is just the geometry that is natural to the surface of a sphere, such as is our own earth, to very good approximation. The surface of a sphere has constant curvature. That just means that the curvature is everywhere the same. To see how the connection to the geometry of 5NONE works, we need only identify the line AGG'G'' with the equator. The perpendiculars we erected to it in the last chapter then just become lines of longitude all of which intersect at the North Pole, that is, at O.
It isn't quite that simple. We do need to adjust our notion of what a straight line is. The essential idea remains the same. A straight line between two points A and B is still the shortest distance between two points. But now we are forced to remain on the surface of the sphere in finding the shortest distance. There is no burrowing into the earth to get a shorter distance between two points. The curve that implements the shortest distance in the surface is known as a "geodesic".
There is a simple way of creating geodesics on the surface of a sphere. They are the "great circles." That is, they are the circles produced by the intersection of the sphere with a plane that passes through the center of the sphere.
In short, the new geometry of 5NONE is just the geometry of of great circles on spheres.
In such a geometry, there are no parallel lines. All pairs of great circles intersect somewhere. That this is so is sometimes overlooked. People sometimes mistake a parallel of latitude for a great circle. In the figure below, points A and B of the same latitude are connected by a parallel of latitude. The parallel of latitude is a parallel to the equator. However it is not the analog of straight line in this geometry, a geodesic. For geodesics are produced by the intersection of the sphere with planes that pass through the center of the sphere. The great circle passing through points A and B is shown in the second figure. It connects A and B by a path that deviates to the North. Since it is the great circle, it is the curve of least distance in the surface of the sphere between A and B.
The great circles are the routes taken by ships and airlines over the surface of the earth, whenever possible, since they are the paths of least distance.
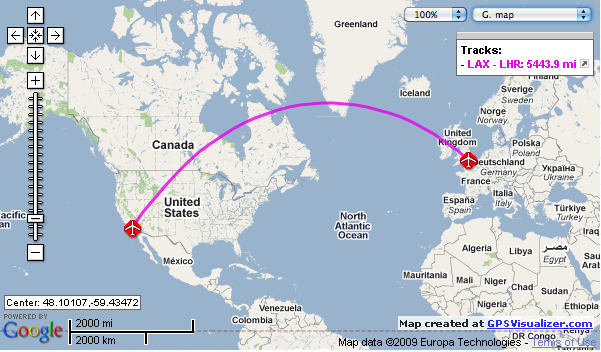
We can now return to the triangles and circles visited earlier. Their properties were radically different from Euclidean triangles and circles. The triangle's angles summed to three right angles and the circle's circumference was only four times the radius. It is now easy to see that these deviations from Euclidean expectations arise only for very large figures on the surface of the sphere. A very small patch of the surface of a sphere is very close to being a Euclidean plane. The calm surface of a small lake on the Earth is very nearly a flat plane; the surface of an ocean is markedly curved. In those very small patches, circles and triangles are very nearly Euclidean in their properties.
The figure below shows a very small equilateral triangle A''B''C''. The sum of its angles will meet Euclidean expectation near enough and be two right angles. As the triangle grows larger, passing through triangle A'B'C' to the huge ABC, the sum of its angles will grow until they are three right angles at ABC.
The situation is the same with circles. The circle around the North Pole below with very small radius OA will meet Euclidean expectations, near enough, and have its circumference 2π times its radius. As the circle grows with radius increasing through OB to OC, the formula will mutate. When the radius is OC, so the circle now coincides with the equator, the circumference will have dropped to being only four times the radius.
| Consider the geometry of 5NONE; that is the geometry that is deducible from the the fifth postulate 5NONE and the other four postulates, suitably adjusted. The expectation of the mathematicians of the eighteenth century and earlier had been that one would eventually be able to deduce a contradiction from them. That is, they expected them to be inconsistent. We started deducing consequences from the postulates but found only odd results, not contradictions. | By contradiction, I mean "A and not A," for A some sentence. So if one's theory allows contradictions to be deduced, the theorist has a very serious problem. It may mean that someone working in dynamics can infer that a system both conserves energy ("A") and does not conserve energy ("not-A"). Which ought the theorist to believe?! |
How do we know that a more imaginative, more thorough analysis might not eventually produce a contradiction? That is, how do we know that the new geometry is consistent?
The question could be answered by a proof of the consistency of the geometry. Alas, advances in twentieth century mathematics have shown that proving the consistency of a rich system in mathematics is typically impossible. However the geometers of the nineteenth century had already supplied us with something that, for practical purposes, is good enough.
In showing that the geometry of 5NONE is really the geometry of great circles on spheres, they provided a relative consistency proof. The idea is simple enough. In a three dimensional Euclidean space, we can recreate or simulate, the different geometry of 5NONE by constructing a sphere. Imagine that somehow we could generate a contradiction within the geometry of 5NONE. That would then mean that we could generate a contradiction within the geometry of great circles on spheres. And that would mean that there must be a contradiction recoverable within the geometry of three dimensional Euclidean spaces.
To get a more concrete sense of how this works, imagine that there is a way of deducing an inconsistency in the geometry of 5NONE. A geometer sits down and begins the steps of the construction that leads to a contradiction. Perhaps the geometer draws a straight line AB; and then a perpendicular to it; and so on. Now imagine a second geometer who works in Euclidean space. That geometer clones exactly everything the first geometer does, but now replaces the first geometer's straight line AB by a great circle through AB on some sphere. The two constructions will proceed analogously for the original geometer working the space of 5NONE and the clone geometer working in the Euclidean space.
 Geometer working with straight lines in geometry of 5NONE. |
 Geometer working with great circles on spheres in Euclidean geometry. |
| Select any two points A and B. | Select any two points A and B. |
| Connect them with a straight line. | Connect them with a great circle. |
| ... ... ... |
... ... ... |
| Contradiction! | Contradiction! |
If the first geometer finds the construction leads to a contradicition, then so must the clone geometer. But that clone geometer is working fully within Euclidean geometry. That is, if the first geometer finds a contradiction in the geometry of 5NONE, then the second must find a contradiction in Euclidean geometry.

So, if the geometry of 5NONE is inconsistent, then Euclidean geometry must be inconsistent. Or turning it around, if Euclidean geometry is consistent, then so must the geometry of 5NONE. Of course the big catch is that we cannot prove that Euclidean geometry is consistent. However we can take some comfort that millennia of investigations have failed to find an inconsistency in it. The relative consistency proof assures us that we are no worse off in the geometry of 5NONE.
What of the geometry of 5MORE? One might imagine that there are many distinct versions according to how many parallels can be drawn through a point not on the original straight line. One can quickly see, however, that there is only one possibility for this number. Imagine, for example, that the geometry allows two parallels AA' and BB' through the point but no more.
Then we can always bisect AA' and BB' with a third line CC'. Now AA' and BB' are parallel to the original line in the sense that they never intersect it, no matter how far they are projected. Since CC' is sandwiched between AA' and BB', the same must be true of it.
The basic idea generalizes. Any attempt to limit the maximum number of parallels allowed by 5MORE fails; we can always add one more. So the geometry of 5MORE is the geometry that arises when we may draw infinitely many parallels through the point not on the original line.
We could continue the exercise of discovering the geometry 5MORE through step by step inference. Since we've seen it done once for the geometry of 5NONE, let us just skip to the final result. It turns out that the geometry of 5MORE is the geometry of a negatively curved surface of constant curvature like a saddle or potato chip.
In this geometry, lines can have infinite length, just as in familiar Euclidean geometry.
However there are differences
that are analogous to those of the geometry of a spherical space:
In very small parts of the space, circles and triangles behave like
Euclidean circles and triangles, near enough.
As the circles and triangles get larger, deviations from Euclidean
behavior emerge. The circumference of circles becomes more than 2π
times the radius; and the sum of the angles of a triangle become less
than two right angles.
The perpendiculars to the equator on the surface of a sphere converge to a single point, the North Pole. On this surface of negative curvature, perpendiculars to a straight line diverge.
It is worth taking a moment to see how at least one of these results follows from the replacing of the postulate of 5ONE with 5MORE. We shall see how it follows that the sum of the angles of a triangle turns out to be less that 180 degrees.
To begin, we consider a straight line AB. At A we erect a perpendicular and mark any point O on the perpendicular. There will be an infinity of straight lines through O that never intersect AB. These lines fill the shaded double wedge shape at O. The wedge is bounded by two lines, the right parallel (OZ) and the left parallel. These are the two most extreme lines through O that never intersect AB. They are both straight lines, although the Euclidean surface on which this figure is drawn cannot properly represent that. Straight lines outside the wedge if produced far enough will eventually intersect with line AB.
Since the space is assumed to be the same in all directions, this double wedge must be symmetric in the left-right direction. It follows that the straight line OZ must meet AO at O at an angle less that 90 degrees. (If it were to meet at 90 degrees, the wedge would collapse to a line and we have returned to the geometry of 5ONE.) This angle AOZ is known as the "angle of parallelism" and is written here as the Greek letter alpha, α. That is:
Angle AOB = α < 90 degrees
For a given length AO, this angle is fixed in size. Its constancy opens the way to constructing a triangle whose angles sum to less than 180 degrees. We now know where to look for such a triangle. It will be found within the space bounded by AB, AO and OZ. We will arrive at it merely by fitting a large enough triangle into the space.
To arrive at a large enough triangle, we will construct an infinite sequence of triangles in the space. To construct them, we mark off equal distances along AB to identify arbitrarly many new points C, D, E, ... We connect O to each of them with straight lines OB, OC, OD, .... (As usual, the lines in these figures are straight lines.)
Now consider the sequence of triangles formed as:
Triangles AOB AOC, AOD, AOE, ...
Each has three angles:
The angle at A is 90 degrees.
The angle at O is always less than the angle of parallelism α.
The angles at B, C, D, ... are small and, as the figure suggests, they
come arbitrarily close to zero degrees.
That is, as we proceed along the sequence, we encounter triangles whose three angles are:
90 degrees, less than α, an angle that comes arbitrarily close to zero
As long as we proceed far enough along this sequence of triangles, this third angle will become close enough to zero for the sum of the three angles to be less than 180 degrees.
This last result is the one sought. To complete its recovery, we need to preclude one complication. The analysis above assumes, but does not show, that the straight lines OB, OC, OD, OE, ... intersect with the straight line AB at points B, C, D, E, ... with angles that decrease such that they come arbitrarily close to zero as we proceed along the sequence. We can show that these angles do grow arbitrarily small if we recall how angles are measured.
!! If you are satisfied that these angles do decrease to be arbitrarily close to zero, you could quite comfortably jump over what follows and proceed to the next section. !!
The angle at O in this figure is measured in radians as follows. We take the length of an arc of a circle subtended by the angle, such as EE', and form the ratio with the circle's radius, EO. That is, we form the ratio EE'/EO.
If we were working in Euclidean geometry, this ratio would be the measure of the angle at O in radians. In non-Euclidean geometries, however, we must consider the sequence of ratios as the radius becomes arbitrarily small:
EE'/EO, DD'/DO, CC'/CO, BB'/BO, AA'/AO, ...
The limiting value of this sequence is the measure of the angle in radians.
To apply this
definition to the triangles constructed, we erect
perpendiculars at B, C, D, E, ... to meet the lines OC, OD, OE, OF, ...
at B', C', D', E', ...
These perpendiculars are close approximations for the circular arcs of the definition of the measure of an angle, when the angles measured are small. This means that we can approximate the radian measure of the angles at C, D, E, F, ... as the ratios:
BB'/BC, CC'/CD, DD'/DE, EE'/EF, ...
The length of these vertical lines BB', CC', DD', EE', ... must decrease to zero, since they must all fit under the parallel OZ that comes arbitrarily close to the produced line AB. However the intervals AB, BC, CD, DE, ... are all equal by construction.
It follows that the ratios BB'/BC, CC'/CD, DD'/DE, EE'/EF, ... come arbitrarily close to zero as we proceed along the sequence. One might imagine that this shows that the measures of the angles at B, C, D, ... decrease to values arbitrarily close to zero. However to secure that result, we need one further step.
The definition of the measure of an angle
requires that we consider a sequence of decreasing
radial distances that come arbitrarily close to zero. To
realize this sequence in the above construction, we must repeat the
entire construction, again and again and again. Each time, we replace
the equal distances AB, BC, CD, ... by equal but shorter distances. The
repetitions are repeated such that these shorter distances come
arbitrarily close to zero. It then follows that the limiting behavior of
the ratios above shows that the angles at B, C, D, E, ... decrease in
radian measure to be arbitrarily close to zero, as required.
The general conception is that we can keep the first four postulates and generate one of the three geometries of 5NONE, 5ONE or 5MORE merely by adopting the appropriate form of the fifth postulate. This general conception is correct but it needs a small technical correction. It arises through the identification of the geometry of 5NONE as the geometry of great circles on spheres. For these great circles are the straight lines of the new geometry. They have properties that are unlike those of the straight lines of the Euclidean geometry of 5ONE and the alternative geometry of 5MORE.
• The first postulate allows us to draw a straight line between any two points. In the new geometry, there are two ways of connecting any two nearby points by a great circle. One goes the short way; the other goes the long way, all around the other side of the sphere.
• The second postulate allows us to produce a straight line indefinitely. That is not possible for great circles. They are already maximally extended. One part of the original notion of the second postulate was that a straight line never really comes to an end. Any point that looks like an end is only a temporary terminus and the line can be extended past it. That lack of a boundary point is all we need for the revised second postulate.
In precluding these properties of straight lines of the geometry of 5NONE, Euclid's postulates are including physical suppositions that ought to be localized to the fifth postulate, either in the version used in 5ONE or 5MORE. It is straightforward to weaken the first two postulates slightly so they still serve their intended purpose, but are now compatible with all three geometries.
The two modified forms of the first and second postulates that accommodate these two alterations are:
1'.
Two distinct points determine at least one straight line.
2'. A straight line is boundless (i.e. has
no end).
The modified postulates are illustrated by the geodesic drawn through two points A and B:
These two modifications may be all that is needed, depending on how we understand the third and fourth postulate.
The third postulate allows us to "... describe a circle with any center and distance." In the geometry of 5NONE, there is a greatest distance that can separate two points. The third postulate can remain as it is as long as we understand "any ... distance" to mean any distance available in the geometry. This is how the "any" is intended. For the same word "any" applies to "center" and has its scope limited to points within the space.
The fourth postulate ("That all right angles equal one another.") can also stand. It applies equally in all three geometries. You might wonder if the definition of a right angle might somehow be supposing Euclidean geometry. However that does not seem to be the case. Euclid's Definition 10 in Book 1 of Elements requires only that we have a notion of equality of angles:
Definition 10.
When a straight line standing on a straight line makes the adjacent angles
equal to one another, each of the equal angles is right, and the
straight line standing on the other is called a perpendicular to
that on which it stands.
We could replace this definition
with a more procedural definition. Let
straight line AB have a midpoint O. Let there be some procedure for
identifying a line CD that passes through O. If the procedure identifies
the same line when A and B are switched, then the line CD is a
perpendicular to AB and the four angles formed are all right angles.
An example of such a procedure is the following.
Draw a circle at O with a radius less than OA. Let it strike AB at A' and
B'. Draw a circle centered at A' of radius A'B' and a circle centered at
B' of radius B'A'. Let the two circles meet at C and D. Draw a straight
line CD connecting C and D and intersecting AB. The procedure gives the
same result if we switch the labels A and B on the two extremities of the
line. Hence the straight line CD is perpendicular to AB. By symmetry, it
must strike AB at O.
My thanks to Balazs Gyenis for prompting corrections in this section.
Copyright John D. Norton. December 28,
2006, February 28, 2007; February 2, 9, 14, September 22, 2008; February
3, March 1, 2010; January 1, 2013. November 18, 2019. January 31,
February 24, 2022.