| HPS 0410 | Einstein for Everyone |
Back to main course page
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
We have already seen that there is nothing terribly
mysterious about adding one dimension to space to form a spacetime.
Nonetheless it is hard to resist a lingering
uneasiness about the idea of a four dimensional spacetime. The
problem is not the time part of a four dimensional spacetime; it
is the four. One can readily imagine the three axes of a three
dimensional space: up-down, across and back to front. But where are we to
put the fourth axis to make a four dimensional space?
My present purpose is to show you that there is nothing at
all mysterious in the four dimensions of a spacetime. To do this, I will drop
the time part completely. I will just consider a four dimensional
space; that is, a space just like our three dimensional space, but with
one extra dimension. What would it be like?
With no effort whatever, I can visualize a three dimensional space--and you can too. What would it be like to live in a three dimensional cube? To be asked to visualize that is like being asked to breathe or blink. It is effortless. There we sit in the cube with its six square walls and eight corners. Our mind's eye lets us hover about inside.
| Can I visualize what it would be like to live in the four dimensional analog of a cube, a four dimensional cube or "tesseract"? I cannot visualize this with the same effortless immediacy. I doubt that you can as well. But that is just about the only thing we cannot do. Otherwise we can determine all the properties of a tesseract and just what it would be like to live in one. There are many techniques for doing this. I will show you one below. It involves progressing through the sequence of dimensions, extrapolating the natural inferences at each step up to the fourth dimension. Once you have seen how this is done for the special case of a tesseract, you will have no trouble applying it to other cases. | Don't be confused by what I am trying to show
here. I am NOT saying that our space is really four dimensional. It
is not. It has only three spatial dimensions. I AM merely trying to
show that we can understand what it would be like if space did
happen to have four dimensions. The exercise is not so different from showing that we can understand what the earth would be like if it had two moons instead of one. It actually has only one moon. But we can figure out in some detail how things would be different if it had two moons. |
The door to the fourth dimension is opening.
The one dimensional analog of a cube is an interval. It is
formed by taking a dimensionless point and dragging it through a distance.
That distance could be 2 inches or 3 feet or anything. Let us call the
distance "L".
The interval has length L. It is bounded by 2 points as its faces--the two points at either end of the interval.
The two dimensional analog of a cube is a square. It is
formed by dragging the one dimensional interval through a distance L in
the second dimension.
The square has area L2. It is bounded by faces
on 4 sides. The faces are intervals of length L. We know there are four of
them since its two dimensional axes must be capped on either end by faces.
So we have 2 dimensions x 2 faces each = 4 faces. The faces together form a perimeter of 4xL in length.
To form a cube, we take the square and drag it a distance L in the third dimension.
The cube has volume L3. It is bounded by faces
on 6 sides. The faces are squares of area L2. We know there are
6 of them since its three dimensional axes must be capped on either end by
faces.
So we have 3 dimensions x 2 faces each = 6 faces. The
faces together form a surface of 6xL2 in area. Drawing a
picture of a three dimensional cube on a two dimensional surface is
equally easy. We take two of its faces--two squares--and connect the
corners.
There are several ways of doing the drawing that corresponds to looking at the cube from different angles. The figure shows two ways of doing it. The first gives an oblique view; the second looks along one of the axes.
So far I hope you have found our constructions entirely
unchallenging. The next step into four dimensions can be done equally
mechanically. We just systematically repeat every step above. The only
difference is that this time we cannot readily form a mental picture of
what we are building. But we can know all its properties!
To form a tesseract, we take the cube and drag it a
distance L in the fourth dimension. We cannot visualize exactly
what that looks like, but it is something like this:
The tesseract has volume L4. It is bounded by
faces on 8 sides. The faces are cubes of volume L3. We know
there are 8 of them since its four dimensional axes must be capped on
either end by faces--two cubical faces per axis. Once again, we cannot
visualize all four of these capped dimenions. We can at best visualize
three directions perpendicular to each other. We then somehow add in the
fourth (in red):
So we have 4 dimensions x 2 faces each = 8 faces. The
faces together form a "surface" (really a three dimensional volume) of 8xL3
in volume. Drawing a picture of a four dimensional tesseract in a three
dimensional space is straightforward. We take two of its faces--two
cubes--and connect the corners.
There are several ways of doing the drawing that
corresponds to looking at the tesseract from different angles. The figure
shows two ways of doing it. The first gives an oblique view; the second
looks along one of the axes.
So now we seem to know everything there is to know about the tesseract! We know its volume in four dimensional space, how it is put together out of eight cubes as surfaces and even what the volume of its surface is (8xL3).
The "drawings" of the tesseract are hard to see clearly.
That is because they are really supposed to be three dimensional models in
a three dimensional space. So what we have above are two
dimensional
drawings of three dimensional models of a four dimensional
tesseract. No wonder it is getting messy!
The images below are stereo pairs. If you are familiar
with how to view them, you will see that they give you a nice stereo view
of the three dimensional model. If these are new to you, they take
practice to see. You need to relax your view until your left eye looks at
the left image and the right eye looks at the right image.
But how can you learn to do this? I find it easiest to
start if I sit far away from the screen and gaze out into the distance
over the top of the screen. I see the two somewhat blurred images on the
edge of my field of vision. As long as I don't focus on them, they start
to drift together. That is the motion you want. The more they drift
together the better. I try to reinforce the drift as best I can while
carefully moving my view toward the images. The goal is to get the two
images to merge.When they do, I keep staring at the merged images, the
focus improves and the full three dimensional stereo effect snaps in
sharply. The effect is striking and worth a little effort.
This pair is easier to fuse:
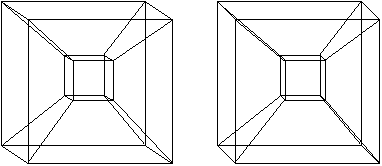
and this one is a little harder:

We can summarize the development of the properties of a
tesseract as follows:
| Dimension | Figure | Face | Volume | Number of faces |
Volume of surface/ perimeter |
|---|---|---|---|---|---|
| 1 | interval | point | L | 1x2=2 | two points |
| 2 | square | interval | L2 | 2x2=4 | 4L |
| 3 | cube | square | L3 | 3x2=6 | 6L2 |
| 4 | tesseract | cube | L4 | 4x2=8 | 8L3 |
If you were to live in a tesseract, you might choose to
live in its three dimensional surface, much as a two dimensional person
might choose live in the 6 square rooms that form the two dimensional
surface of a cube. So your house would be the eight cubes that form the surface
of the tesseract. Imagine that there are doors where ever two of
these cubes meet. If you are in one of these rooms, how many doors would
you see? What would the next room look like if you passed through one of
the doors? How many doors must you pass through to get to the farthest
room? How many paths lead to that farthest room? Could you have any
windows to outside the tesseract? What about windows to inside the
tesseract?
Some of these questions are not easy. To answer them, go back to the easy case of a three dimensional cube with faces consisting of squares. Ask the analogous questions there and just extrapolate the answers to the tesseract.
Access to a fourth dimension makes many things possible that would otherwise be quite impossible. To see how this works, we'll use the strategy of thinking out a process in a three dimensional space. Then we replicated it in a four dimensional space.
Consider a coin lying in a frame on a table top.
|
There is no way the coin can be removed from the frame within the confines of the two dimensional surface of the table. Now recall that we have access to a third dimension. The coin is easily removed merely by lifting it into the third dimension, the height above the table. We are then free to move the coin as we please in the higher layer and then lower back to the tabletop outside the frame. |
|
The thing to notice about the lifting is that the motion does not move the coin at all in the two horizontal directions of the two dimensional space. So the motion never brings it near the frame and there is no danger of collision with the frame.
| Now repeat this analysis for its analog in one higher dimension, a marble trapped within a three dimensional box. |
|
| Now finally consider two linked rings in some three dimensional space. Can we separate them using access to a fourth dimension? |
| It can be done by exactly the same process of lifting one of the rings into the fourth dimension. As before, note that the lifting does not move the ring in any of the three directions of the three dimensional space holding the initially linked rings. So the motion risks no collisions of moved ring with the other. The lifting simply elevates the moved ring to a new three dimensional layer of the four dimensional space in which no part of the other ring is found. The moved ring can then be freely relocated in that new layer and, if we pleased lowered back into the original three dimensional space in quite a different location. |
Now comes the knotty challenge. We are familiar in our three dimensional space with tying knots in a rope. Some knots are just apparent tangles that can come apart pretty easily. Others are real and can only be undone by threading the end of the rope through a loop. So take this to be a real knot: one that cannot be undone by any manipulation of the rope if we cannot get hold of the ends. (Imagine, if you like, that they are each anchored to a wall and cannot be removed.)
The challenge is to convince yourself that there are no real knots in ropes in a four dimensional space. The principal aid you will need is the manipulation above of the linked rings. To get yourself started, imagine how you would use a fourth dimension to untie some simple knot you can easily imagine.
Does the general idea of "lifting" an object into the fourth dimension still seem elusive? If so, here's a technique for visualizing it that may just help. The trick is to imagine that differences in position in the extra dimension of space can be represented by differences of colors.
|
Here's how it works when we start with a two dimensional space and lift into the third dimension. The objects in the original two dimensional space are black. As we lift through the third dimension, they successively take on the colors blue, green and red. |
| Now let's apply this colored layer trick to the earlier example of lifting a coin out of a frame. The coin starts in the same two dimensional space as the frame. We lift it up into the third dimension into a higher spatial layer that we have color-coded red. In this higher layer, the coin can move freely left/right and front/back without intersecting the frame. We moving it to the right until it passes over the frame. Then we lower it back down outside. |
| Now imagine that we cannot
perceive the third dimension directly. Here's how we'd
picture the coin's escape. It starts out inside the frame in the
space of the frame. It is then lifted out of the frame into the
third dimension. At that moment, it is indicated by a ghostly
red coin. Its spatial position in the left/right and
front/back direction has not changed. All that has changed is its
height. It is now in the red height layer. If we move the coin left
or right, or front and back, in this red layer, it no longer
intersects the frame and can move right over it. We won't see it
move over the frame, however. As far as we are concerned it will
just move through it.
The motion of the coin in this third dimensional escape passage is illustrated by the ghostly red coin. |
| This last analysis of the coin in the frame is the template for dealing with the real case of a marble trapped inside a three dimensional box. If the marble moves in any of the three familiar dimensions (up/down, left/right and front/back), its motion intersects the walls of the box and it cannot escape. So we lift the marble into the fourth dimension, without changing its position in the three familiar dimensions. In the figure, this is shown by the marble turning ghostly red. In the red space, the marble is free to move up/down, left/right and front/back, without intersecting the box's walls. The marble then moves so that is passes over one of the walls. It is then lowered out of the red space back to the original three dimensional space of the box, but now outside the walls. |
| The same analysis applies to the linked rings. One ring is lifted out of the three dimensional space of the original set up. In this red space, the ring can move freely without intersecting the other ring. We move it well away from the other ring and then drop it back into the original three dimensional space. It is now unlinked from the other ring. |
Copyright John D. Norton. February 2001;
July 2006, February 2, 2008; February 6, 2012; April 30, 2014. January
30, 2022.