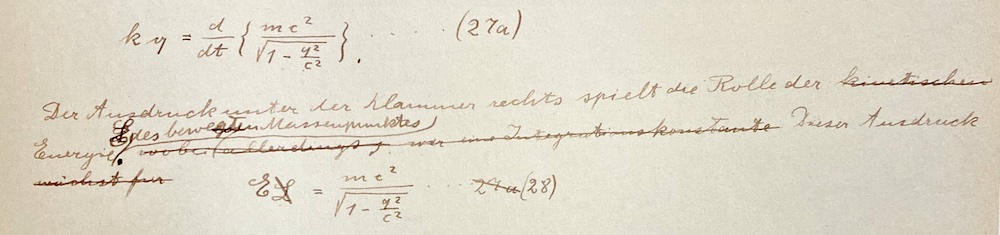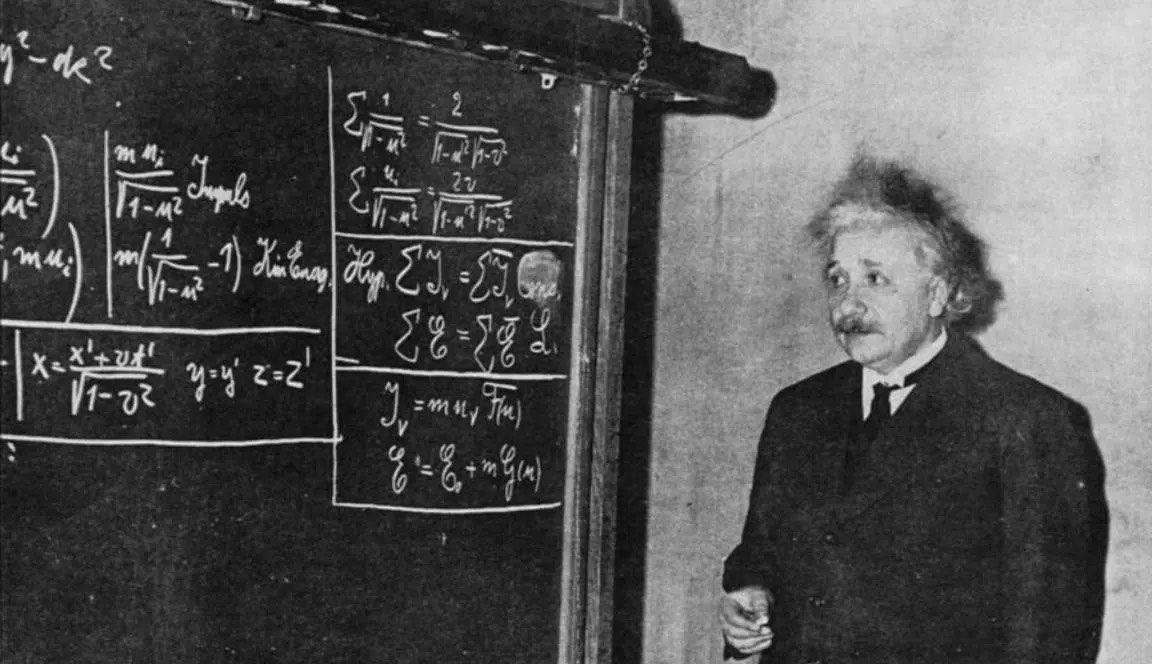| HPS 0410 |
Einstein for Everyone |
|
Back
to main course page
E=mc2
John
D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Einstein's famous equation has grown into one of the great
symbols of the 20th century. It is the one equation in science that people
recognize, if any is. It has a kind of iconic status
and dual connotations: the brilliance and insight of Einstein and the
darkness of atomic bombs. Images.
The Idea
The basic idea behind the formula E=mc2 is easy to state. Mass and energy are really just the same thing. At first that seems impossible.
•
Mass is a measure of the quantity of stuff and manifests as a resistance to acceleration. A body with little mass, like a pebble, is easy to set in motion.

A more massive body like a big stone is harder to set in motion, precisely because it has more mass.

• Energy seems to be something entirely different. We are familiar with it in many forms. There is the heat energy of a fire:

https://commons.wikimedia.org/wiki/File:Fire02.jpg
Or the electrical energy of a lightning bolt:

https://commons.wikimedia.org/wiki/File:Lighting_barrage.jpg
Or the energy of motion of rapidly moving locomotive:

https://commons.wikimedia.org/wiki/File:Ferrocarril_Mexicano_Locomotive_No._2872_(29886964471).jpg
The relation tells us that, contrary to superficial appearances, mass and energy are just the same thing.
Whenever there is mass present, there is energy. A pebble is just energy in a very concentrated form. Each unit of mass is also c2 units of energy. And that is a huge amount of energy since c2 is so huge.
Whenever there is energy present, there is also mass. When a body is heated by the energy of fire, it also gains mass. Each unit of energy corresponds to a gain of 1/c2 units of mass. And that is a very tiny amout of mass since 1/c2 is so small.
Put most briefly, Einstein's equation says that energy
and mass are really just two different names for the same thing.
They rise and fall together because they are at heart the same thing. We
like to call that thing mass when it is in hard, lumpy forms like bricks.
We prefer to call it energy when it is in the form of radiation. But the
one is just a form of the other.
The sameness is not so different from a more familiar sameness. Ice, liquid water and steam all seem superficially to be different things. Ice is hard. Water is fluid. Steam is vaporous. But they are all water, just in different forms.
Einstein's Afterthought
The relation E=mc2 is a central part of Einstein's special theory of relativity, In 1905, however, it appeared as an afterthought. Einstein's "On the Electrodynamics of Moving Bodies" was submitted to Annalen der Physik on June 30, 1905. Einstein's "Inertia of Energy" paper that proposed E=mc2 was submitted almost three months later on September 27, 1905. It was not entitled "E=mc2" but rather asked the question "Is the energy content of a body dependent on its inertial?" Of course, the answer was "yes." It is a short paper of just three pages and here is the entire text:



A quick scan of the text shows that the equation E=mc2 is not there. The main idea is there, however, but in another form. The colored text on the third page gives the formulation Einstein used:
"If a body loses energy L in the form of radiation, then its mass decreases by L/V2."
where Einstein is using "V" for the speed of light.
More generally, Einstein's result was expressed in a slightly more restricted form than we now might use:
Changes in the energy in a body correspond to changes in the body's inertial mass, in the ratio of one unit of energy to 1/V2 units of mass. This leaves open the possibility that bodies might have a portion of their mass that is independent of their energy. That possibility was soon discarded.
| A few years later, in a manuscript of 1912 describing his developing ideas on relativity, Einstein wrote the relation in a more familiar guise. Here is the formula in Einstein's handwriting ("autograph" as the manuscript experts say). It is the first time the formula appears in manuscript pages we now have. |
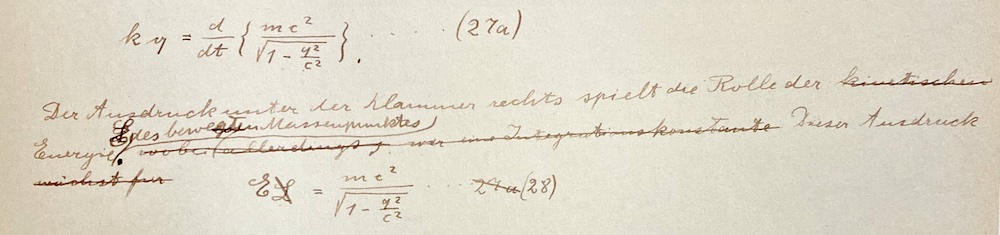

We can see that Einstein has crossed out the "L" used for energy in his 1905 paper and replaced it with the now standard "E." However he is still writing "q" for speed that we would now write as "v."
The text surrounding the formula says:
"The expression in the
brackets at right [in formula (27a)] plays the role of the energy E of the moving point mass. This expression [(28')]
[formula (28')]
, [page break]
grows to infinity, if [the speed] q approaches the value c; therefore it would require an infinite expenditure of energy to impart the speed c to the body...."
Here's another example of Einstein's writing of E=mc2 in a letter to Ludwik Silberstein in 1946. The letter sold at auction in 2021 for $1.2million. The content is summarized on a website as "Einstein calculates the mass difference between a system of two equal masses (represented by M) that are an infinite distance from another. Einstein continues the equation, calculating the same two masses a specific distance (R) apart and orbiting a centre of mass."

The Electrodynamic Background
It may now seem strange that such a momentous result was presented so tersely as an afterthought. However, in 1905, things looked different. The idea that energy and mass were connected somehow was already a familiar idea in electrodynamic theory. For example, consider a beam of light. In the theory of Einstein's time, that light beam would be conveying energy to anything it fell upon. So far the result is not so surprising. We are all used to sunlight warming us on a sunny day. However the novel result was that the light beam was also applying a pressure to the objects upon which is falls. More colloquially, it "pushed them." The pressure--the push it gives--is, of course, extremely small and nothing we can notice. But the electrodynamic theory of Einstein's time needed it in order to preserve familiar conservation laws. If light could exert a pressure, then it must also be conveying momentum (to be discussed below) and was, perhaps, not so different from a rain of particles of some type.

What was missing in the theory of the time was the idea that the connection is universal so that is applies to all forms of mass and energy. The point of Einstein's paper was simply to assert the generality of the result. It likely seemed a lesser result to him them than it does to us now.
Why E=mc2? Kinematics and Dynamics
Why do we have this relation between energy and mass in special relativity? The short answer is that it is an unavoidable consequence of the two principles Einstein used as the foundation of special relativity. So far we have seen how these two principles require us to modify our notions of space, time and motion. We have not yet considered how the two principles affect our ideas about forces and causes of motion. If we ask how they are to be modified, E=mc2 follows.
So far we have looked at kinematics,
the study of motions in space and time, We now need to pay attention to dynamics, the causes of motion.
| In kinematics, all our analyses are given solely
in terms of the quantities measuring positions in space and time and
the other quantities that can derived from them. If we know when some body is where and how long it takes to move from place to place, then we also can determine its speed, its velocity (=speed in a particular
direction) and its accelearation.
A familiar problem is to describe when (at what time) a moving planet
is where (in space). We learned from Kepler that the
motion of planets is along elliptical orbits. What was subsequently called his "second law" tells us that a planet moves faster when it is closer to the sun. The law is that a radial line drawn from the sun to the planet sweeps out equal areas in equal times,
|

Berry History of Astronomy 1898 p. 186
|

From F. Halliday, An Easy Introduction to Fortifications and Gunnery. London, 1774. |
We learned from
Galileo that bodies in free motion above the
earth's surface move along parabolas. One of the major discoveries of kinematics is that, for the same
initial speed, the longest horizontal distance covered results when the motion is
initially elevated at 45 degrees to the horizontal. This is a foundational result in gunnery and also applies to more mundane applications like tennis.
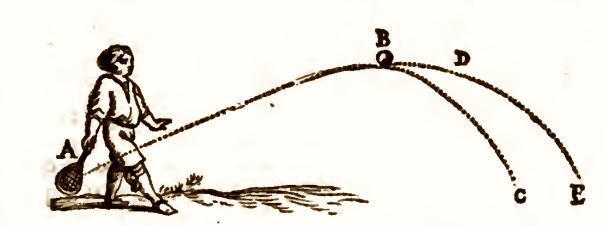
From Descartes, Epistolae, 1682 p. 359 |
Now consider dynamics,
the study of the causes that bring about motion, where those causes
are forces. E=mc2 arises as part of the modification to
dynamics brought about by Einstein's theory.
In dynamics we expand our analyses
to include new quantities associated with the causes of motion. The
most important is force and two
quantities derived from it, energy and
momentum.
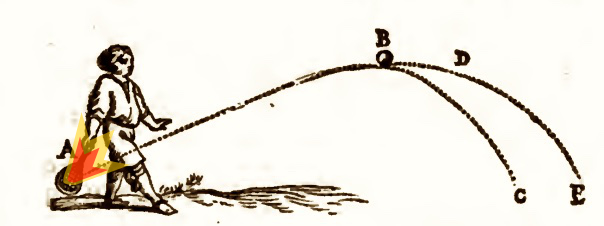
We no longer just note that a tennis balls moves in a parabolic
trajectory over the net. We also ask how hard we have to hit it--how
much force we must apply--to send it along the desired trajectory.
For the case of a cannonball, we now also ask how much gunpowder we
need to load into the cannon so that the force of its explosion will
send it on the desired trajectory. We want to know the energy and
momentum imparted to the cannonball. It is the delivery of that
energy and momentum to the target that wreaks its destructive
effect.

 |
 |
In kinematics, special relativity changes our normal
expectations. We find that the timing of events and distances and times
elapsed are judged differently by observers in relative motion. Most
relevant for the present topic, we find that we cannot accelerate anything
through the speed of light. We have to adjust our ideas about space and
time to accommodate this result. Since all these motions have causes
treated in dynamics, we must make corresponding changes in our theories of
these causes, to preclude the possibility of accelerating bodies through the speed of light. When we make these changes in dynamics, E=mc2
results. We shall now see how that comes about.
Classical physics and special
relativity agree in the following framework of basic concepts.
That is, they both employ the concepts of energy, momentum and force and
they both respect the two relations stated below that obtain between them.
Energy: I know of no useful definition for energy.
It is understood by example. When systems
interact, they exchange energy. For example, a moving car has a certain
energy of motion that is converted to heat energy in the brakes when the
car is slowed. That energy originally came from chemical energy stored in
the gasoline fuel, which in turn was supplied as light energy to the
plants that became petroleum.
 |
Momentum: The momentum of a moving body is
a measure of the quantity of motion. It is defined by
momentum = mass x
velocity
for a mass moving at the nominated velocity. The formula contains
both mass and velocity since the quantity of the motion increases
with both. (Which is the greater motion: an ounce of lead moving at
100mph or a pound of lead moving at 100 mph?) Unlike energy, it is associated with a direction in space, since velocity is speed in some definite direction. A quantity of momentum is not fully specified until that direction is given. |
Force: When two bodies interact, the force measures
the rate of transfer of momentum and energy between them. That is, it measures the
intensity of an interaction. It is roughly equivalent to the
pre-scientific notion of muscular effort. A push can set a heavy cart in
motion because it applies a force to it. Its size is given by the rate of
transfer of energy and momentum
If
a constant force acts on a body, force, energy and momentum are
related by the simple relations:
Momentum gained by body
= Force x Time during which force acts
Energy gained by
body = Force x Distance through which force acts
These relations obtain in both classical and relativistic physics. We
shall see, however, that in the relativist context they turn into E=mc2.
Conservation of Energy and Momentum
The most important laws in dynamics are those that state
the conservation of energy and of momentum. These two laws can be applied
whenever we have a closed system; that is, a
system that does not interact with its surroundings. They assert that for
such systems and any process they may undergo:
Total
Energy
at start |
= |
Total
Energy
at end |
|
Total
Momentum
at start |
= |
Total
Momentum
at end |
An isolated spaceship in deep space
is a good example to consider. Imagine some interaction that takes place
within that system. These laws tell us that the total of energy before the
interaction equals the total of energy afterwards; and the total of
momentum before the interaction equals the total of momentum afterwards.
 |
Let's look at an example of such a process. A spacewalker stands
on the spaceship and both are at rest.
They have no velocity, so their total momentum is zero.
Momentum
=mass x velocity
=mass x 0 = 0 |
Now imagine that the spacewalker
vigorously pushes off from the spaceship and floats off into
space. The spacewalker has gained some momentum. If the spacewalker has
mass of 200 pounds and moves off at 10 feet per second, he has gained
2,000 units of momentum. The law of conservation of momentum demands that
the total momentum of the two systems stays constant. That is the total
momentum of the spaceship plus spacewalker system must remain zero.

That can only happen if the spaceship gains a negative
momentum exactly opposite to the momentum gained by the
spacewalker. That is a momentum of -2,000 units. Then the sum of the two
will be zero.
-2,000 + 2,000 = 0
That will only happen if the spaceship gains
a velocity in the direction exactly opposite to that of the
spacewalker's motion; that is, if the spaceship recoils. So
conservation of momentum demands a
recoil.
|
Analogous considerations apply to the combined
energy of the spaceship and spacewalker. After the interaction both
spaceship and spacewalker have some energy of motion. That energy
originated as chemical energy stored in the muscles of the spacewalker,
before the spacewalker used muscle power to push off the spaceship. The
energy of motion gained by the system must match the chemical energy lost
from the spacewalker's muscles so that the total
energy stays constant.
Achieving Unlimited Velocities in
Classical Physics
Unlike relativity theory, classical physics allows us to
accelerate bodies to arbitrarily high speeds. There is a simple mechanism
for achieving these unlimited speeds in classical physics. If we keep
applying a constant force to a body, the body
will keep gaining energy and momentum and its velocity will rise
accordingly.


This cathode ray tube is a traditional "Crookes tube." Electrons are drawn from a cathode at the left by an electric field of several thousand volts between it and the anode in the tube at the side. Some electrons move so fast that their inertia carries them past the anode to strike the rightmost end of the tube, where they produce light by fluoresence.
https://commons.wikimedia.org/wiki/File:Crookes_tube_two_views.jpg |
How can we go about applying a constant force to
a body over a long enough time period to achieve very high
velocities? If the body is very small, it turns out to be much
easier than you might imagine. If the body is a very small
particle--an electron say--then the forces of an electric field can quite quickly accelerate
the particles to close to the speed of light.
Over a hundred years ago, this happened in the first cathode ray
tubes, that is, in devices like old fashioned TV tubes. If a high
voltage is applied between two metal plates in a near evacuated
vessel, the electric field resulting from the voltage is quite
capable of pulling electrons off one electrode at very high speeds.
This same technique is still used today in particle
accelerators in which various particles are accelerated to
close to the speed of light by combinations of electric and magnetic
fields. |
What about accelerating ordinary objects up to very high
speeds by ordinary means? What about the most familiar method of all,
swatting a ball with a bat or a club? You might suspect that this
procedure is self-defeating. If I want to swat a ball to get it to move
quickly, wouldn't I need a faster moving bat to swat
it with? And once it is moving fast, wouldn't I need a yet faster moving
bat to get it to move still faster? So can the method only yield high
speeds if I already have something moving at even higher speeds?
These worries turn out to be misplaced. It is easy to see
that a small ball at rest, hit by a much heavier bat, will be accelerated
to twice the speed of the bat. This, for example, is
pretty much what happens when a golf club hits a golf ball. The greatest
speed the ball can achieve is twice that of the club's head. The argument
that shows it is much easier than you would expect and uses the principle
of relativity to make it simple. Look here
for details.
Here's what we find happens when a small mass is struck by
a very heavy mass moving at 100,000 miles per
second. If the collision is elastic, the mass is boosted to 200,000 miles
per second.

It also turns out that it is quite easy to imagine systems
that use repeated collisions to accelerate bodies, according to
classical physics, to arbitrarily high speeds. Here's one simple set up.
We have two very massive blocks rolling towards one another on rails. A
small elastic body is trapped in between them. Perhaps it is suspended by a rope from
a high support. It is set in motion by a collision with one of the blocks.
The body then bounces back and forth between the two approach blocks.

With each bounce, according
to classical physics, the body gains the same increment of speed and same
increment in the magnitude of its momentum.

By choosing the sizes and distances carefully, we can set
things up so that there are as many collisions as we like. While the mass
bounces back and forth between the approaching blocks, the collisions
happen more and more rapidly and the mass
goes faster and faster. According to classical physics, this arrangement
is quite able to accelerate the mass past the speed of light, as long as
the blocks are massive enough and the materials strong enough not to break
in the violent collisions.
These schemes illustrate how it is possible, according to
classical physics, to impart unlimited momentum
to a body and, as a result, to boost it to unlimited velocities, including
those greater than that of light.
We have seen that relativity theory prohibits boosting bodies past the
speed of light. Therefore we must pay attention to how
it arises in classical physics. Then we can decide how we must
modify classical dynamics, so that it does not allow us to accelerate
objects through the speed of light.
| Momentum |
= |
mass |
x |
velocity |
increases
without limit |
|
fixed |
|
increases
without limit |
Recall that momentum is mass x velocity. Since the mass is
a fixed number, characteristic of the body, if the
body's momentum increases, so must its velocity. If its momentum
grows without limit, then its velocity also increases without limit. As a
result, classical physics tells us that we can accelerate masses through
the speed of light.
The Unlimited Momentum Loophole
Closed
In relativistic physics, we
can also supply unlimited momentum to a body. Indeed we can use the same
mechanism as in classical physics--just set up a small object to collide
with a larger one. And with successive collisions, we can supply more and
more momentum to the small object. More generally, just applying a constant force to a body for long enough will increase its momentum without limit in virtue of the relation above.
Momentum gained by body = Force x Time during which force acts
However, as we saw in the case of just
one collision, these processes will never accelerate the small object past
the speed of light.
Somehow we have to make sense of this prohibition on
accelerating objects through the speed of light. We still have the
relation, momentum = mass x velocity. We can increase the momentum without
limit. So why doesn't the velocity also increase
without limit?
In the classical context, getting to the conclusion of
unlimited velocity depended on an assumption: the mass of the object is
constant. That is the only assumption we have left to adjust. That is how
relativity theory requires dynamics to be modified. The mass of the
object increases with its velocity. Schematically:
increases
without limit |
|
|
|
increases
only as
far as c |
| Momentum |
= |
mass |
x |
velocity |
|
|
SO...
mass must
increase
when velocities
get
close
to c |
|
|
As we put more and more momentum into the body, the
velocity ceases to rise without limit; the mass
starts
to rise instead. Eventually, once the velocity has come close
to that of light, all the increase is associated with the mass. This
effect on a mass, as we repeatedly double its momentum, is shown in the
table:
| Momentum |
Mass |
Velocity
(in units of 1,000
miles/sec) |
| 0 |
1 |
0 |
| 118.6 |
1.186 |
100 |
237.2
=118.6x2 |
1.621 |
146.4 |
474.4
=237.2x2 |
2.740 |
173.2 |
948.8
=474.4x2 |
5.198 |
182.5 |
1897.6
=948.8x2 |
10.251 |
185.1 |
3795
=1897.6x2 |
20.43 |
185.8 |
7590
=3795x2 |
40.82 |
185.9 |
| ... |
... |
... |
| ∞ |
∞ |
c=186 |
The
formula used to determine the mass m is here.
In sum, according to relativity theory, a
force--no matter how big or long acting--cannot accelerate a body through
the speed of light. The closer the body gets to the speed of light, the
greater its mass becomes and the harder it gets to accelerate. The mass
grows without limit.
In 1905, this was not
such a shocking way to view things. There was already a well-established tradition in both theory and experiment in which accelerations through the speed of light were found impossible.
The theory arose from treatments of charged bodies in electrodynamics. Electrons--then referring to both postively and negatively charged particles--were modelled as spheres of electric charge. When these electrons acquired high speeds, what was then described as an electrodynamic effect impeded their motion. The impeding effect grew without limit as the speed of light was approached so that the electrons could not be accelerated through the speed of light. It was as if the electrons were becoming more massive. The electrons were said to have acquired an "electromagnetic mass." It was then thought not to be a real mass, but just an effect that looked like an added mass.
Exactly how this electromagnetic mass grew with speed depended on details assumed for the structure of electrons. They were commonly assumed to be spheres of electric charge. Two of the most prominent theories were those of Max Abraham and H. A. Lorentz. In Abraham's theory, electrons preserved their spherical shape as they approached the speed light (shown at left). In H. A. Lorentz's theory, electrons contracted in the direction of motion (shown at right), using the same contraction as was required to account for the null result of the Michelson-Morely experiment.

That rapidly moving electrons acquire an electromagnetic mass was also then affirmed through careful experiments. The best known of these were carried out by Walter Kaufmann. He experimented with cathode rays--that is beams of negatively charged electrons--and also with the beta "β" rays produced by the radioactive decay of radium. These β rays were also beams of negatively charged electrons and could exceed 90% the speed of light.

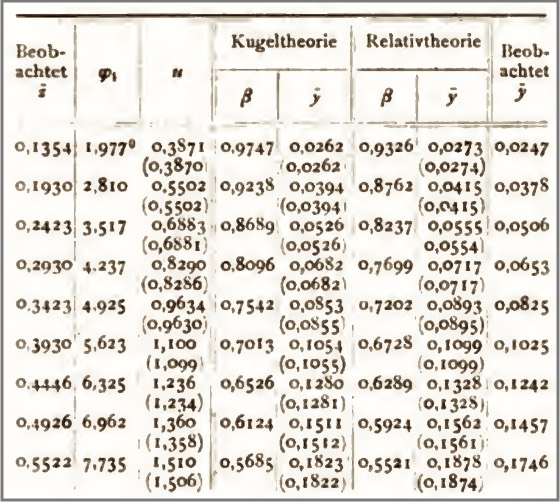 |
Here is a 1906 summary of Kaufmann's experimental results prepared by Max Planck in 1906. (Physikalische Zeitschrift, 7(1906), pp. 753-62.) The results are for electrons moving at over 50% the speed of light up to the high 90's%. In the table, β is the fraction of the speed of light. It varies 0.5521 to 0.9747.
The table does not report masses directly. Rather, it reports the magnitude of the deflections of the rays by magnetic fields "z" and by electric field "y." Those experimentally measured deflections determine how much mass an electron has gained. A more massive electron is deflected less.
The table reports observed deflections ("beobachtet") and predictions made by the two theories. The "sphere theory" ("Kugeltheorie") is Abraham's theory. "Relative theory" ("Relativtheorie") is H. A. Lorentz's theory. By 1906, it was recognized that Einstein's 1905 theory of relativity gave the same predictions in these experiments as Lorentz's theory. So Planck used Relativtheorie as a convenient label for both.
The outcome, awkward for Einstein and Lorentz, was that the experiments favored Abraham's theory over Einstein and Lorentz's. Later reseach, however, vindicated the Einstein-Lorentz predictions. |
For more on how the kinematics of relativity blocks a scheme for using
collisions to boost things through the speed of light, see this account of
the Resolution of Collisions in Classical
and Relativistic Physics.
E=mc2 for Kinetic Energy
When we apply sufficient force to a body for sufficient time, we accelerate it to a speed that is arbitrarily close to the speed of light; and we communicate arbitrarily large quantities of momentum to it. The same process communicates arbitrarily large quantities of energy to the body. The governing relation was given above for the application of a constant force:
Energy gained by body = Force x Distance through which force acts
During this process, the mass of the body also becomes arbitrarily large. There is a simple relationship between the amount of kinetic energy the body gains and the mass the body gains. Because of its importance, we can pause to break it into pieces:
Add 1 unit of energy → Add 1/c2
units of mass
Add 2 units of energy → Add 2/c2 units of mass
etc.
More generally:
Add E units of energy → Add E/c2
units of mass
Turning this around, we can say:
Add 1 unit of mass → Add c2 units of energy
Add 2 unit of mass → Add 2c2 units of energy
etc.
More generally:
Add m units of mass → Add mc2 units of
energy
This is Einstein's celebrated
equation: E = mc2 for the important case of one particular sort of energy, the kinetic energy of motion. We shall see shortly that it can be generalized to all forms of motion. It turns
out that the relation for kinetic energy can be derived in this case with very little more
fuss merely by combining the two relations we saw above for energy,
momentum and force.
See The World's Quickest Derivation of E = mc2
Einstein's Hesitation
 |
The relation presented above between kinetic energy and mass was already present in Einstein's 1905 "On the Electrodynamics of Moving Bodies." However Einstein did not identify it as such and perhaps did not realize just what his relation said. It arises in the concluding Section 10 "Dynamics of the Slowly Accelerated Electron." Einstein calculated the kinetic energy "W" gained by an electron that is accelerated to a speed "v." The formula Einstein recovered is shown at left.
While the formula has a suggestive "mc2" in it, it must be read with caution. The m is the mass of the electron when it is at rest. This m must be multiplied by the remaining expression in the curly brackets to convert it to the mass gained.
Einstein then concluded, as expected, that "velocities greater than of light ... have no possibility of existence." For an impossible infinity of energy would be needed merely to accelerate the electron to the speed of light. |
| The above pages are from the standard, English translation of Einstein's 1905 "On the Electrodynamics..." The notation in the original German, shown at right, was different. Einstein used the Greek mu, μ, for the rest mass and an upper case V for the speed of light, instead of c. |
 |
 |
Why did Einstein not identify this relation as our modern E=mc2? We can only conjecture, but there is a very obvious conjecture. In the 1905 "On the Electrodynamics...", Einstein used a different definition of mass from the one we now use (and the one he soon adopted). The relation E=mc2 does not hold for this alternative definition of mass. Einstein was explicit in defining mass through the relation
force = mass x acceleration
If this definition is adopted, then the mass of a rapidly moving body differs according to whether the force is applied parallel to the direction of the body's motion or transverse to it. What results are two different magnitudes, "longitudinal" and "transverse" mass. In 1905, this definition conformed with the then current analyses of the rapidly moving electrons. |
The later practice is to define the mass of an electron through the relation
force = rate of change with time of (mass x velocity)
One then recovers a single number for the mass, independently of the direction of the force applied. It is this conception of mass that enters into the relation
E=mc2. Einstein's later "On the Inertia of Energy" paper derives what we now call E=mc2 for the mass of an electron at rest. In this special case, longitudinal and transverse masses reduce to the same number.
E=mc2 for all forms of energy
So far, we have seen that when a body gains or loses kinetic energy E is also gains or loses a mass, m = E/c2. The general result is that this holds for all forms of energy. Whenever energy is transfered in any form from one body to another, mass is also transferred in an amount conforming with E=mc2.
For example heat energy from a red hot poker might be transfered to heat water that boils to make steam; and the steam turns a turbine that powers a generator that makes electrical energy that charges a battery.

• When the red hot poker loses heat energy, it also loses a corresponding amount of mass.
• When the water gains the heat energy from the poker, the water gains a corresponding amount of mass.
• When energy is carried by the steam in its temperature and pressure, the steam gains a mass corresponding to the magnitude of the energy.
• When the steam powered generator produces electrical energy from the energy of the steam, there is a corresponding increase in the mass of generator.
• When the generator charges the battery so that it holds a charge in the form of chemical energy, the battery increases in mass in a corresponding amout.
This is the general result. How can we show it to be correct? A simple way is to amplify the reach of the one case we already know. That is, we know that E=mc2 holds for kinetic energy. Can we show that if kinetic energy is transformed into a different sort of energy, then E=mc2 still holds. That is, if we have a system harboring some other form of energy, when it gains or loses energy E, must is also gain or lose mass m = E/c2?
To begin, let us take a small particle whose mass at rest ("rest mass") we will set to unity and accelerate it to a speed very, very, very close to the speed of light.

The closer it comes the speed of light, the greater portion of its mass is due to kinetic energy:
Speed = 90% light rest mass = 1 mass from kinetic energy = 1.3
Speed = 99% light rest mass = 1 mass from kinetic energy = 6.1
Speed = 99.9% light rest mass = 1 mass from kinetic energy = 21.3
Speed = 99.99% light rest mass = 1 mass from kinetic energy = 69.1
Speed = 99.999% light rest mass = 1 mass from kinetic energy = 222.6
In the following, we will neglect the contribution of the particle's rest mass to the total mass since moving the particle arbitrarily close to the speed of light enables us to make that contribution arbitrarily small, in proportion to the total mass
If we write the energy of the particle as "energy," its mass acording to E=mc2 is:
mass of particle = energy / c2
We can now calculate the momentum of the particle in the direction of its motion as:
momentum = mass x velocity =
(energy / c2) x c = energy / c
Now assume that we have a device that can absorb this particle and convert its kinetic energy into some other form of energy. It might be heat energy, or electrical energy, of chemical energy, or the energy of a rotating body. Or it might be some combination of all these types of energy and others still. The device, at rest in our frame of reference, absorbs this rapidly moving particle.

After the absorbtion, the device has gained all the kinetic energy of the particle and converted it to some other form of energy:

We would like to determine whether the energy gained by the device has increased its mass. The simple way to make the determination is to examine how the momentum of the device has changed. What complicates the determination is that the device will recoil slightly from the momentum imparted by the particle and will gain some motion in the same direction as the motion of the particle. That means that the momentum gained will manifest in two ways: as the addition of mass and also in the motion of the recoil. We would have to untangle these to determine the mass gain.
The determination will be much easier if we can somehow suppress that recoil motion. There is an easy way to do this. It was used by Einstein in his 1905 E=mc2 paper "Is the energy content of a body dependent on its inertial?". Divide the kinetic energy equally over two particles that approach the device from opposite sides at equal speeds:

While each particle will impart momentum to the device when it is absorbed, the momenta will be in opposing directions and thus cancel. There is no recoil and the device remains at rest, while the device has gained the energy of the two particles:

To complete Einstein's clever approach, we now resdecribe the same process of absorbtion in a new inertial frame of reference in which the totality of the system moves at a speed "v." In the figure, the motion is vertical.

In the first frame of reference, the device does not recoil after the absorbtion of the particles. It remains at rest. Hence, after the absorbtion, the device persists unchanged in it vertical motion at v in the new frame of reference.

While the device does not alter its motion, it has still gained momentum from the incoming particles. To determine the momentum gained, we recall that the energy delivered to the device has been divided over the two particles. Each carries energy of
(1/2) x energy
Corresondingly, each carries a momentum of
(1/2) x energy/c.
These two quantities of momentum are at least partially oriented in opposite directions. So, when they are absorted by the device, they partially cancel each other out. The parts cancelled are those aligned in the horizontal direction in the figure. The parts that do not cancel are those aligned in the vertical direction.
For each particle, a fraction v/c of its momentum, energy/c, is directed vertically.

That means that each particle delivers a vertically directed momentum to the device of
(1/2) (energy /c) x (v/c) = (1/2) (energy /c2) x v
That is, the absorbtion of "energy" leads the device to gain momentum in the vertical direction of
(1/2) (energy /c2) x v + (1/2) (energy /c2) x v = (energy /c2) x v
The momentum of the device in the vertical direction is just
momentum = mass x velocity
Since the velocity of the device has not altered in the absorbtion, it follows that all the gain in momentum is manifested as mass. Comparing the last two formulae, we have
mass gained by device = (energy gained) / c2
This is the general result sought. The device has gained a quantity of energy from the kinetic energy of the particles and has converted it into another form of energy. The device has been specified sufficiently expansively so that these other forms of energy can be of any type. No matter what that type is, the device has gained a mass equal to energy/c2, in accord with E=mc2.
This last analysis tells us that gains in energy conform with E=mc2. What if a system loses energy? We can quickly see that there will be a loss of mass corresponding to E=mc2. We need only assume that the device can be modified so that it emits two particles that move at speeds very close to that of light. The analysis above is then essentially unchanged, except that the transfers of energy and momentum are in the opposite direction.

We then recover:
mass lost by device = (energy lost) / c2
Einstein's 1905 Derivation
This last derivation of E=mc2 is very close to the one used by Einstein in 1905. The first difference is that Einstein did not use very rapidly moving, massive particles to impart energy to or remove energy from the device. Instead, he imagined a body that loses energy by emitting two systems of plane electromagnetic waves, in opposite directions. A standard result in electrodynamic theory of the time is that the momentum carried by a system of plane electomagnetic waves is just
momentum of electromagetic waves = energy / c
This is the same relation as we used above for a massive particle moving very, very close to the speed of light. Hence we could duplicate the analysis just given, but using light as the vehicle for the imparting or removing of energy.

While Einstein could have done this, he did not. His analysis of 1905 was substantially more complicated. We have already seen mu conjecture over the reason for this in the discussion above of Einstein's Hesitation. Einstein was still using the older notions of longitudinal and transverse mass.
In this first decade of the new century, Einstein gave several more demonstrations of the inertia of energy. They were distinctive in all using some relations about the energy and momentum of electromagnetic radiation. This opened the possibility of a misreading of his result of the inertia of energy. One might mistakenly think that it is somehow inseparably connected with electrodynamics. This misreading did eventually worry Einstein enough that he later offered a demonstration of E=mc2 that was independent of electrodynamics. It is the demonstration discussed below that is associated with his talk in Pittsburgh of December 1934.
Here is the introductory paragraph in which he explains his reasons for this new derivation.

E = mc2 and Atomic Energy
http://en.wikipedia.org/wiki/File:Nuclear_fission.svg |
E=mc2 governs processes that convert energy into mass and mass into energy. What is most important for practical purposes is
that the conversion factor c2 is a
huge number. That means that a small amount of mass under
conversion yields a huge amount of energy. This is the principle
behind atomic energy, nuclear weapons and nuclear power. generation
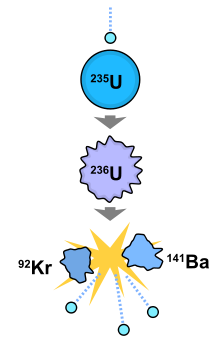
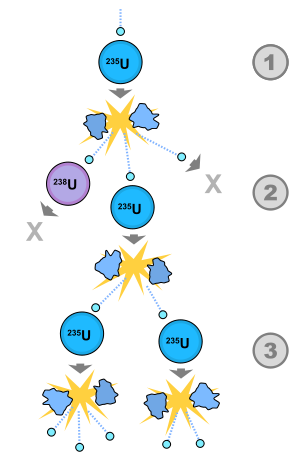
In a nuclear fission reaction, a Uranium-235 atom nucleus
"fissions"--that is splits--into atomic nuclei of smaller size and
other particles such as neutrons. It turns out that the total mass
of these decay products is just slightly less than the mass of the
Uranium nucleus we started with. This mass
defect is around a tenth of one percent of the mass. This
missing mass has been converted into energy. Because c2
is so large, the result of converting even a small part of the mass
into another form is the release of a huge amount of energy. But
because each Uranium nucleus is so very small, the energy released
when one nucleus splits is still small. |

http://en.wikipedia.org/wiki/File:Nagasakibomb.jpg |
Now things get interesting. What triggers a
Uranium-235 atom nucleus to fission is an impact by a neutron. When the
nucleus splits, it releases more neutrons, such as the two or three
in the reactions shown. If there are enough Uranium-235 nuclei in the vicinty, these neutrons can then initiate the fission
of further Uranium-235 nuclei; and the resulting neutrons initiate the
fission of still further Uranium -235 nuclei. This will be the case if we have suitably enriched Uranium, that is, Uranium in which the portion of the isotope Uranium-235 has been sufficiently increased. In this case, if nothing restricts this
process, we have an uncontrolled chain
reaction that releases a huge amount of energy. That is an
atom bomb.
|
http://en.wikipedia.org/wiki/File:Nuclear_fission.svg |

http://commons.wikimedia.org/wiki/File:Fat_man.jpg
If, however, we introduce moderators that absorb the
neutrons, we can slow down the chain reaction so that we have a controlled
release of heat. That heat can be used to do useful things like boil water
to make steam to drive electric generators. Then we have a nuclear
power plant.

http://commons.wikimedia.org/wiki/File:Cooling_towers_of_Dukovany_Nuclear_Power_Station.jpg
One gram of matter, about 20
drops of water, if it were fully converted into electrical energy, would
be 25,000,000 kilowatt hours of electrical energy. That is enough energy
to power a 100 watt light bulb for 250,000,000 hours or 28,500 years.
Recorded history extends only about 12,000 years.

At 5 cents a kilowatt hour, it would cost $1,250,000 if
purchased from a utility company. The energy of that same gram, if
released in an explosion, would be equivalent to 21,000 tons of TNT.











Image:
http://en.wikipedia.org/wiki/File:Gluehlampe_01_KMJ.png
Einstein's Skepticism over Atomic Power
In 1905, Einstein did not expect this sort of application of his result,
which then seemed to be purely of theoretical interest. That skepticism persisted as late as 1934. During a December visit to Pittsburgh, Einstein was interviewed about the possibility of atomic energy providing useful power. Read the Pittsburgh Post_Gazette article of December 29, 1934, for the full report. His denial of the possibility is reported early in the article. Later in the article he is reported as saying:
Like Shooting in the Dark
"It's like shooting birds in the dark in a country where there are only a few birds," he said, illustrating his belief that molecule transfers which would necessary to atomic power systems are too improbable for practical mechanical use.
"We have no means to force the transfers which do not consume more energy than the transfers give out," he said.
Einstein's skepticism did not last. With the impending outbreak of World War II, Leo Szilard, Edward Teller and Eugene Wigner were alarmed at the prospect of the axis powers gaining atomic weapons. They induced Einstein to sign the famous collaborative letter of August 2 1939 that urged President Roosevelt to provide US government support for atomic weapons research.

Hear Einstein Explain It
Click here.
Here are some rare photos of Einstein actually giving a lecture in which he derives E=mc2. It was on December 28, 1934 in Pittsburgh at what was then the Carnegie Institute of Technology, but is now Carnegie Mellon University. It was the Eleventh Josiah Willard Gibbs Lecture, at a joint meeting of the American Mathematical Society, the American Physical Society and Section A of the Americal Association for the Advancement of Science. He spoke in what is now the Kresge Theater, but was then the Little Theaters. See this. The derivation was published as Albert Einstein, "Elementary derivation of the equivalence of mass and energy," Bull. Amer. Math. Soc. 41(4): 223-230 (April 1935).


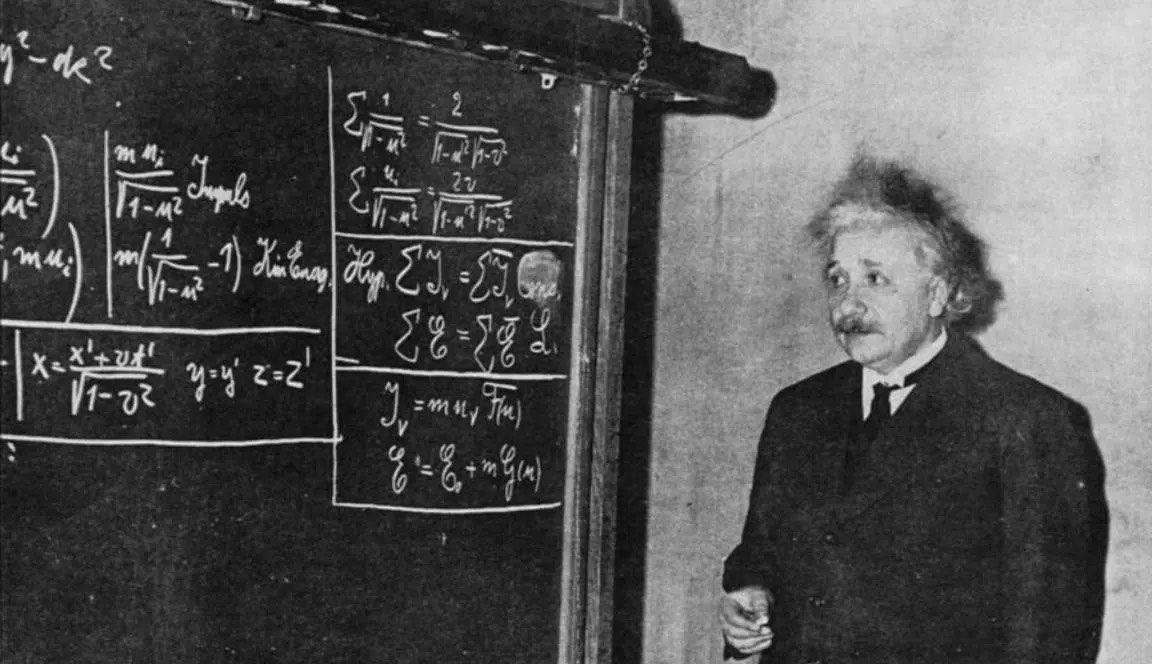

larger version
What You Need to Know
- The notions of energy, momentum and force and how they are related.
- The conservation of energy and momentum and how to apply them.
- How greater than c speed is achieved in classical physics and why
these methods fail in relativity theory.
- What happens to the mass of a body as c is approached.
- What E=mc2 says and how it is applied.
Copyright John D. Norton. January
2001, September 2002. July 2006, January 11, September 23, 2008, January
12, 2012; January 22, May 8, 2015. January 21, 2022. Substantial revisions, February 3, 2024.