| HPS 0410 | Einstein for Everyone | Spring 2010 |
Back to main course page
For submission
Consider the candidate morals in the the chapter, The Philosophical Significance of the Special Theory of Relativity.
1. Which, if any, do you find most convincing? If you answer "none of the above," propose an alternative.
2. In your own words, give a clear a statement of the moral.
3. State clearly the argument in favor of the moral.
For discussion in the recitation
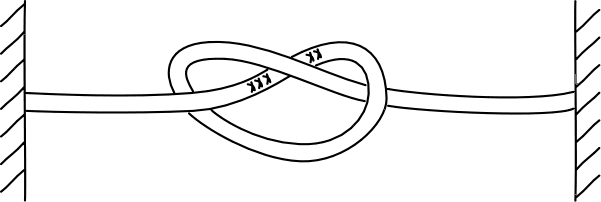
A. Consider the two challenges in "What is a four dimensional spacetime like?" The second is to show that there are no knots in a four dimensional space. Use the techniques described to show that if the knot shown were in a four dimensional space, the knot could be untied without detaching the ends of the rope from the walls.

Hint: consider the section of the rope marked "XXXXX." What if it were lifted into the fourth dimension?
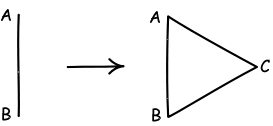
B. An equilateral triangle is a plane figure bounded by three lines of equal length. It is drawn by taking a line AB and a point C not on AB. The points A and B are connected to C with straight lines. C is selected so that all three lines AB, AC and BC are equal in length.
A regular tetrahedron is is a three dimensional solid bounded by four equilateral triangles. It is drawn by taking an equilateral triangle ABC and a fourth point D. The points A, B and C are connected to D by straight lines. D is selected so that each of the triangles ABC, ABD, BCD and ACD are equilateral.
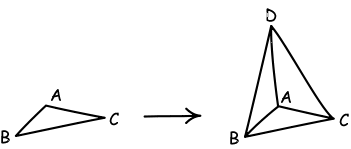
Continuing in this pattern, what does a four dimensional tetrahedron look like? How is it constructed? Draw one.
(For the brave to tackle outside the recitation: Compute the area and volume of an equilateral triangle and a regular tetrahedron. Continue to compute the four dimensional volume of the figure drawn in B. Warning: This is a hard problem. I have not found a simple way of doing it!)