| HPS 0410 | Einstein for Everyone | Spring 2008 |
Back to main course page
For submission Monday March 3/ Tuesday March 4.
1. What is the difference between extrinsic and intrinsic curvature?
2. Imagine that you are a two dimensional being trapped in a flat two dimensional surface.
(a) How would you use geodesic deviation to confirm the flatness of your surface?
(b) Imagine that a three dimensional being picks up your surface and bends it into cylinder, without in any way stretching your surface. (This is just what happens when someone takes a piece of paper and rolls it into a cylinder.) You are still trapped in the surface. If you now use geodesic deviation to determine the curvature of your surface, would you get the same result as in (a)? Explain why.
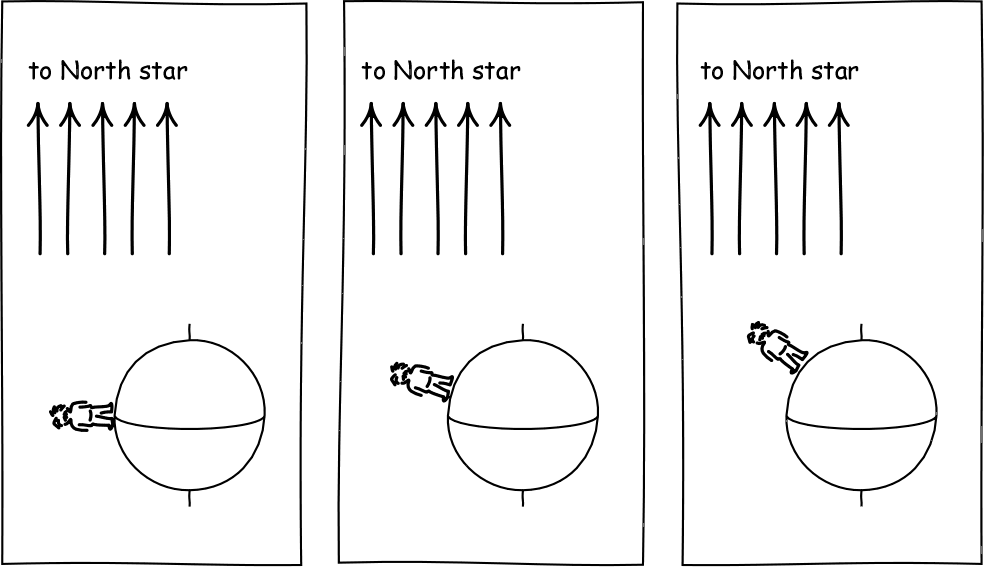
3. In antiquity, it was observed that the position of the northern pole star changed as the observer's position changed in the north-south direction. Specifically, for each 69 miles = 111km that the observer moved northward, the pole star raised in elevation by one degree.
(a) Explain how this observation enabled ancient astronomers to argue that the surface of the earth is curved.
(b) Use it to estimate the circumference of the earth.
(c) Explain why this observation enables the establishing of extrinsic curvature.
(d) Explain why this observation, by itself, does not enable us to infer the intrinsic curvature of the earth's surface. (Hint: Is there a shape with extrinsic curvature, but no intrinsic curvature that exhibits the effect?)

4. In a space with three or more dimensions, the curvature need not be the same in every two dimensional sheet that passes though some point in the space. Of course sometimes things are simple and the curvature does work out the same. Here's an example. Imagine that you are in an ordinary, three dimensional Euclidean space. You slice the space up into the flattest two dimensional sheets you can find, all built out of intersecting straight lines. The first set of sheets run left-right and up-down. The second set of sheets run left-right and front-back. The third set of sheets run up-down and front-back. You use geodesic deviation to determine the curvature of the sheets in each set. What is the curvature of:
(a) The left-right and up-down sheets?
(b) The left-right and front-back sheets?
(c) The up-down and front-back?
(d) Things need not work out so simply. In what space discussed in the chapter would the results be different?
For discussion in the recitation.
A. Here's an exercise that shows how geodesic deviation can be used to determine how much curvature a surface has, not just whether it is zero, positive or negative. Geodesic deviation can be used by observers on the surface of a planet to determined whether they are on an earth sized planet or on one twice its size with correspondingly different curvature.
(a) Two observers stand on the earth's equator 100 miles apart. They begin to move northward. After traveling 100 miles they find that they are closer by 169 feet. How is this effect is related to the curvature of the earth's surface.
(b) If they had started 200 miles apart and moved 100 miles due north, by how much would they have approached each other? Convince youself that your answer is correct by drawing a figure.
(c) Imagine that, before the observers start their motions, the earth is inflated to twice its size so that its radius of curvature has doubled. The observers of (a) are carried along with the inflation, like two ants sitting on a balloon. They now start 200 miles apart. After they have moved 200 miles due north, by how much would they have converged? (Hint: get the answer just by scaling up everything in (a)!)
(d) Use your answer to (b) to convince yourself that the result of (c) could not happen on an earth of the original size, so that the amount of convergence can be used to determine if the surface is the earth's or a planet of twice its size.
Technical note: What makes these computations
messy is that the amount of convergence increases with the square of
the distance the observers travel north. The formula is
Convergence = (1/2)x(east-west distance at equator) x (distance moved
north)2 / (radius of earth)2
where the formula holds only as long as the two distances are very small
compared to the radius of the earth. This formula can be inverted to
determine the radius of the earth from local measurements of the other
distances in the formula.
B. Here's an example that illustrates how curvature can vary in different directions. Consider the extruded spherical space discussed here at the close of the chapter on non-Euclidean geometry. Imagine that somehow you have been transported into this space. You want to figure out which are the east-west, left-right and up-down directions in this space. To do so, you label three perpendicular directions "X," "Y" and "Z." You slice the space into three different types of two dimensional sheets. The XY sheets contains the directions X and Y; and so on for XZ and YZ. You now have three sorts of sheets in which you can carry out geodesic deviations measurements. Let us say you end up with the following results:
XY sheet: geodesics converge
XZ sheet: geodesics neither converge nor diverge
YZ sheet: geodesics neither converge nor diverge
(a) What sort of curvature does each of the three sheets have?
(b) Which of X, Y and Z directions can correspond to east-west, north-south and up-down? Explain how you arrived at this identification.