| HPS 0410 | Einstein for Everyone | Fall 2008 |
Back to main course page
For submission Tues Oct. 14 , Wed. Oct. 15
1. Consider a geometry in which Euclid's 5th postulate is replaced by:
Through any point NO straight line can be drawn parallel to a given line.
Show that there is at least one triangle in this geometry whose angles sum
to more than two right angles.
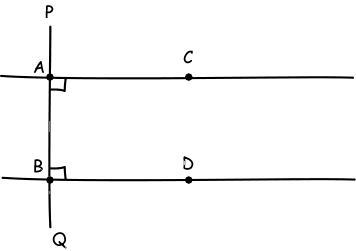
Hint: On a line PQ, select two points A and B. Construct lines AC and BD
perpendicular to PQ. What happens if AC and BD are extended in both
directions?

2.In a Euclidean space, what is
(a) the sum of the angles of any triangle;
(b) the circumference of a circle with radius 10,000 km;
(c) the area of a right angled triangle if the length of the sides enclosing
the right angle are both 10,000 km?
3. The geometry of 1. above,
suitably treated, is the geometry of the surface of a sphere. The Earth is,
to good approximation, a sphere of circumference 40,000 km.
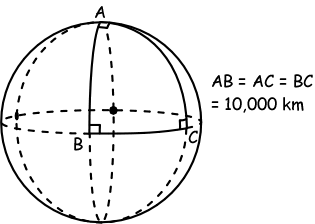
(a) On this sphere, what is the sum of the angles of a triangle all of whose
sides are 10,000 km? (An example of such a triangle is shown as triangle ABC.
It has one vertex at the North Pole and extends down to the equator.)
(b) What is the circumference of a circle of radius 10,000 km in this
surface?
(c) The triangle ABC is a right angled triangle all of whose sides are 10,000
km long. What is its area? (Reminder: The area of the Earth is 509,300,000
sq.km.) Compare your answers in question 2 and 3.
4. If you had before you a two
dimensional surface of constant curvature, how could your determine whether
the curvature was positive, negative or zero by measuring
(a) the sum of angles of a triangle;
(b) the circumference of a circle of known radius?
5. How could you check whether our
three dimensional space has a positive, negative or zero curvature by
measuring
(a) the sum of angles of a triangle;
(b) the surface area of a sphere of known radius?
For discussion in the recitation.
A. Does it make sense to say that a space has a curved geometry if there is no higher dimensioned space into which the space can curve?
B. In the context of Question 5, how might we go about measuring the sum of the angles of a triangle in our actual space? Remember, ordinary measurements of things in our actual space conform closely to Euclidean geometry. Architects routinely build skyscrapers using Euclidean geometry. Therefore, if our actual space turns out not to be Euclidean, the amount of curvature would have to be very, very small. We would need a very, very accurate way of measuring the angles of a triangle for this test. Only then would we be able to tell if the sum is really 179.9999 degrees or 180.00001 degrees. What might such a very, very accurate means be?
Hint, if our space has some curvature, the deviation from 180 degrees in the sum of the angles of a triangle becomes greater the larger the triangle. That makes the detection of deviations from Euclidean geometry easier.
C. The discovery of non-Euclidean geometries eventually precipitated a crisis in our understanding of what has to be and what just might be the case. At one extreme are necessities, such the truths of logic; they have to be true. At the other extreme are mundane factual matters--contingent statements that may or may not be true. Somewhere in between is a transition. Locating that transition has traditionally been of great importance in philosophy and philosophy of science. For if something is necessarily true, we need harbor no doubt over it. If something is contingent, the mainstream empiricist philosophy says we can only learn it from experience. Sometimes the contingent proposition is very broad. For example, consider the proposition that there never has been and never will be a magnet with only one pole. We may come to believe this proposition with ever greater confidence. But we can never be absolutely certain of it. We never know whether tomorrow will bring the counterexample.
Just where should the transition between necessity and contingency come?
Here is a list of propositions that begins with logical truths and bleeds off into ordinary contingent propositions. Sort them into necessary truths and contingent propositions. How are you deciding which is which?
If A and B are both true, then A is true.
If one of A or B is true and A is false, then B is true.
For any proposition A, either A is true or A is not true.
1 + 1 = 2
7 + 5 = 12
There are an infinity of prime numbers.
Every circle has one center.
The sum of the angles of a triangle is two right angles.
Only the fittest survive.
Every effect has a cause.
Every occurrence has a cause.
No effect comes before its cause.
Improbable events are rare.
Energy is always conserved.
Force equals mass times acceleration.
The earth has one moon.