| HPS 0410 | Einstein for Everyone | Fall 2008 |
Back to main course page
For submission Mon. Sep 15, Tues. Sep. 16, Wed. Sep. 17
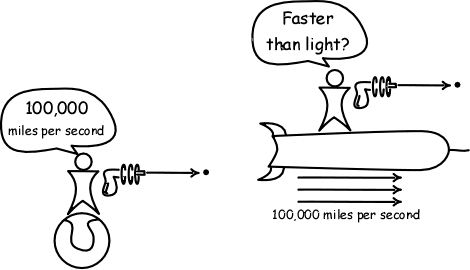
1. Two spaceships pass a planet, moving in opposite directions. A planet observer judges each to be moving at 100,000 miles per second. An observer on one of the spaceships measures the speed of the other spaceship.

(a) According to classical physics, what speed will that spaceship observer measure for the other spaceship? Is this speed faster than light?
(b) According to relativity theory, what speed will that spaceship observer measure for the other spaceship? Is this speed faster than light?
2. (a) What is the momentum of a body with a given mass and velocity?
(b) What happens in classical physics to a body when its momentum is increased?
(c) What happens in relativistic physics to a slowly moving body when its momentum in increased?
(d) What happens in relativistic physics to a very rapidly moving body when its momentum is increased?
3. How does your answer to 2. relate to the impossibility of accelerating bodies through the speed of light in relativity theory?
4. How does your answer to 2. relate to the
famous equation Energy = mass x c2?
For discussion in the recitation.
A. The planet observer of question 1. above watches the first spaceship observer measure the speed of the second spaceship by means of a procedure that uses rods and clocks. Would the planet observer judge that measuring procedure to be a fair one that gives the correct result?
B. Imagine that you have a gun that can fire a particle at 100,000 miles per second. You are in a spaceship moving at 100,000 miles per second with respect to the earth. You point the gun in the direction of your motion and fire. Would an earthbound observer judge the particle to travel at 200,000=100,000+100,000 miles per second? Show that the earthbound observer could not since that would violate the principle of relativity, when that principle is combined with the light postulate. How rapidly would you (the spaceship observer) judge the particle to be moving?
C. When a golfclub strikes a golfball, the ball is accelerated to a higher velocity than that of the club head. Classically, with a heavy club head and a perfectly elastic golfball, the ball can be impelled to twice the speed of the club head. Might a sufficiently robustly constructed club and ball, wielded with sufficient speed, be able to accelerate the ball past the speed of light?
What kinematical effects in special relativity block this means of accelerating something past the speed of light?
What dynamical effects in special relativity block it?
D. What does the law of conservation of mass say? What does the law of conservation of energy say? In classical physics, these are two separate laws. What becomes of them in relativity physics?
E. When an electric battery is charged, what
happens to its mass?
When a hot body cools, what happens to its mass?
When a spring is compressed what happens to its mass?
Inside a completely isolated spacestation, an electric battery is used to
warm the hands of an astronaut and to run a motor that winds a spring. What
happens to the total energy of the spaceship? What happens to the total mass
of the spaceship?
F. When an atom of Uranium-235 undergoes fission and breaks into parts, the total mass of the parts is less than the mass of the original atom. What happens to the missing mass? Why is this missing mass important in modern life?
G. The arguments we have investigated show that relativity theory prohibits us accelerating an object past the speed of light. Do any of them rule out objects that have always been traveling faster than light (or, possibly, were created initially already moving faster than light)?