| HPS 0410 | Einstein for Everyone | Fall 2008 |
Back to main course page
For submission Mon. Sep. 8, Tues. Sep. 9, Wed. Sep. 10.
For Einstein, the big breakthrough in his work on special relativity came when he found a way to reconcile the principle of relativity and the light postulate. He recognized that these principles only seemed irreconcilable because of an unwarranted assumption that we routinely make about space and time. We assume that all observers should agree on which events are simultaneous. Instead, Einstein noticed, we may allow for the possibility that observers in relative motion may disagree about which spatially separated events are simultaneous. This assumption of the relativity of simultaneity allowed him to retain both the principle of relativity and the light postulate. This assignment will help you to see how.
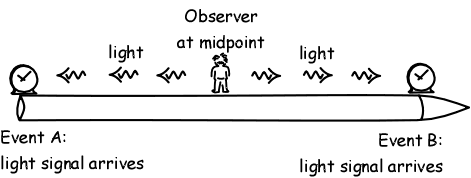
1. An observer is at the midpoint of a long spaceship. At the same instant he sends light signals to both front and rear of the spaceship. Event A is the arrival of the signal at the rear; event B is the arrival of the signal at the front.
(a) Are the two events A and B simultaneous according to the spaceship observer?
(b) Imagine that there are two good clocks located at the front and the rear of the spaceship and the arrival of the signals is used to reset each clock to the same time. Are the clocks now properly synchronized according to the spaceship observer?

(c) The spaceship is moving rapidly in the direction of its length past a planet. An observer on the planet watches the signaling procedure described above. Does the planet observer judge events A and B to be simultaneous? If not, which happens first?
(d) Does the planet observer judge the two clocks to be set in proper synchrony? If not, which is set ahead of the other?
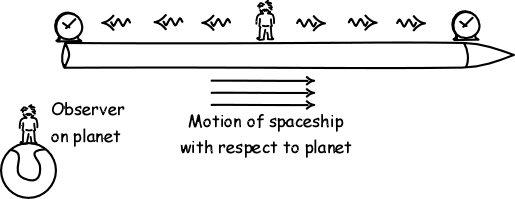
2. A light signal flashes back and forth between the two ends of the same spaceship. If the light postulate is to hold for the spaceship observer, then the spaceship observer must judge that the light travels at the same speed in all directions. That is, according to the spaceship observer, the signal must take the same time to travel from front to back as from back to front. Assume this transit time is one minute. Then the arrival times of the light signal must be registered as 12:00, 12:02, 12:04, ...etc. at the rear of the ship and 12:01, 12:03, 12:05, ... etc. at the front.
(a) Assume the light postulate also holds for the planet observer. Will the planet observer judge the transit time for the forward trip of the light signal to be the same as the transit time for the backward trip? If not, which is longer?
(b) How can the planet observer reconcile the answer to 2.(a) with the readings on the clocks of the moving spaceship that record the transit times for the light signal?

For discussion in the recitation.
A. Two observers I and II both stand on a large platform. There are two lightning strikes, A and B.
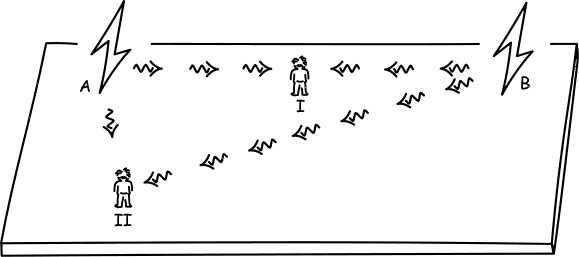
The observer I is located at the midpoint of the spatial locations of the strikes A and B. Light signals coming from the strikes A and B arrive at this observer I at the same time.
The observer II is located much closer to the strike A. As a result, the light signal from strike A arrives at observer II much earlier than the light signal from strike B.
Observer I sees the signals at the same time; observer II sees them at different times.
Is this difference the relativity of simultaneity of relativity theory? If not, why not?
B. Two identical spaceships pass one another, moving rapidly in opposite directions at the same speed according to an observer on a nearby planet. The planet observer judges that both spaceships have shrunk the same amount due to relativistic length contraction. So they are the same length and, in conformity with this expectation, the planet observer notes that the two spaceships line up perfectly as they pass.
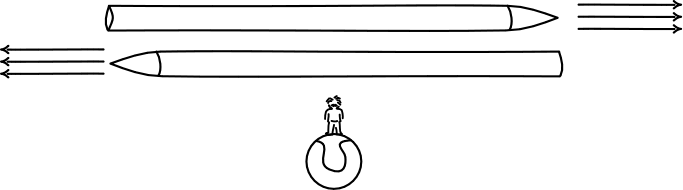
An observer on one of the spaceships, however, finds the other spaceship to be moving rapidly. So that spaceship observer judges the other spaceship to have shrunk relative to the first spaceship. And an observer on the second spaceship comes to the reverse judgment, that the first spaceship has shrunk.
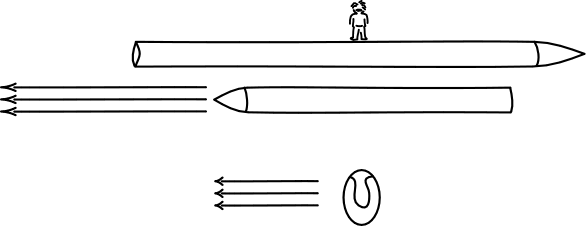
How is it possible for all of of them to come to such different judgements?
C. Judgments of simultaneity are involved in any procedure that measures the length of moving bodies or the times elapsed for processes on them. Consider some procedures for measuring such lengths and times and show how judgments of simultaneity are hidden in them. What if, for example we measure the length of a moving body by timing how long it takes to pass a single observation point, where we use just one clock to time its passage. Its length is just its speed multiplied by the time measured.