| HPS 0410 | Einstein for Everyone | Spring 2007 |
Back to main course page
For submission Tuesday March 27, Wednesday March 28.
1. (a) How does Einstein's cosmological constant λ modify his original gravitational field equations of 1915?
(b) Show how the term can be re-interpreted as representing a form of matter in space.
(c) Why is the form of matter odd?(Hint: use the fact that Einstein' universe and a de Sitter universe both use the term essentially to introduce a form of matter is governed by a gravitational repulsion.)
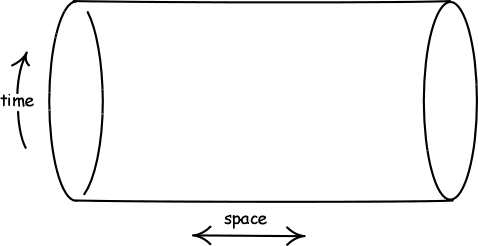
2. Imagine a time-travel, cylinder universe which is empty except for one mass.
(a) Draw in the worldline of the mass when it remains at rest in the space and reconnects with itself.

(b) Draw the worldline of the mass when the mass moves to the right.

(c) The mass can collide with its future self. The collision is such that the mass gets deflected by just the right amount to come back as the later self of the collision. Draw the worldline that shows this, recalling that aside from collisions the mass moves inertial--i.e. in a straight line in the space.

For discussion in the recitation.
A. If we were in a universe that admits time travel, that possibility might be manifested as an odd global constraint. How might such a constraint appear? How might we use it to convince ourselves we are in a time travel universe?
| B. Imagine a Minkowski spacetime wrapped up in one spatial direction. A space traveler synchronizes his clock with one on earth and then leaves earth. The traveler moves inertially eventually coming back to earth without ever changing direction. When the traveler's clock and the earth clock are compared, the traveler's clock will be found to have been slowed by the motion and will read less than the earth clock. Is this a violation of the principle of relativity? Shouldn't the traveler expect the earth clock to have run slower? (Hint: this space has a preferred state of motion!) | 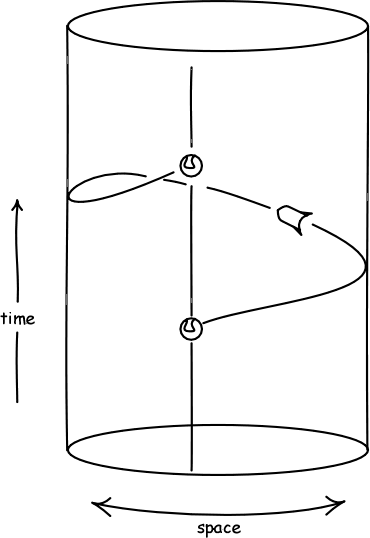 |