| HPS 0410 | Einstein for Everyone | Spring 2007 |
Back to main course page
For submission Tuesday March 13/ Wednesday March 14.
1. The extrinsic curvature of a surface is its curving within a higher dimensioned space. The intrinsic curvature of a surface is a deviation from a flat geometry fully within the surface.
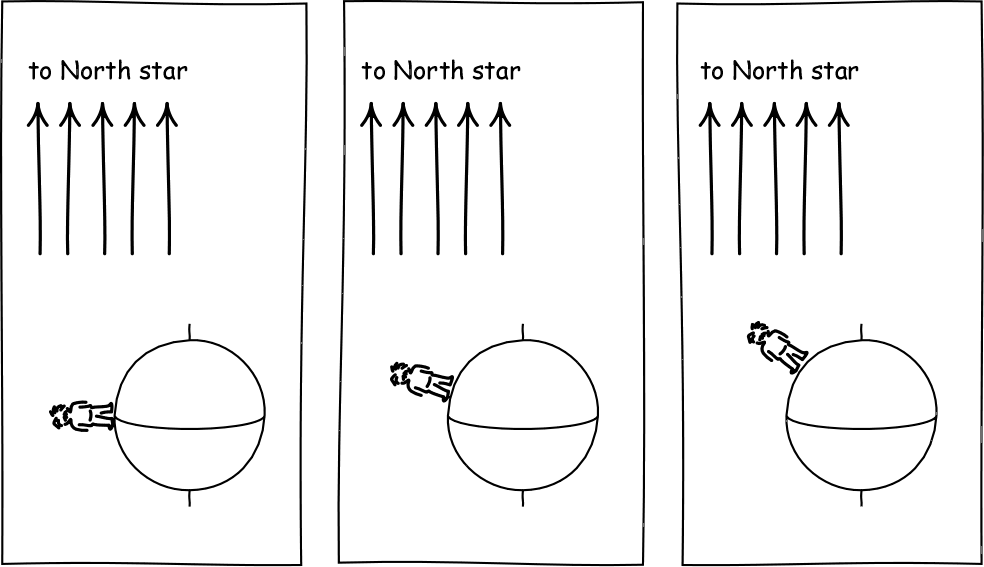
In antiquity, it was observed that the position of the northern pole star changed as the observer's position changed in the north-south direction. Specifically, for each 69 miles = 111km that the observer moved northward, the pole star raised in elevation by one degree.
(a) Explain how this observation enabled ancient astronomers to argue that the surface of the earth is curved.
(b) Use it to estimate the circumference of the earth.
(c) Explain why this observation enables the establishing of extrinsic curvature.
(d) Explain why this observation, by itself, does not enable us to infer the intrinsic curvature of the earth's surface. (Hint: Is there a shape with extrinsic curvature, but no intrinsic curvature that exhibits the effect?)

2. (a) Two observers stand on the earth's equator 100 miles apart. They begin to move northward. After traveling 100 miles they find that they are closer by 169 feet. Explain how this effect is related to the curvature of the earth.
(b) If they had started 200 miles apart and moved 100 miles due north, by how much would they have approached each other? Convince youself that your answer is correct by drawing a figure.
(c) This effect of "geodesic deviation" can be used to determine the intrinsic curvature of the surface on which the observers are located. Imagine that the earth were inflated to twice its size so that its radius of curvature has doubled. The observers of (a) now start 200 miles apart. After they have moved 200 miles due north, by how much would they have converged? (Hint: just scale everything up!)
(d) Use your answer to (b) to convince yourself that the result of (c) could not happen on an earth of the original size.
Technical note: What makes these computations
messy is that the amount of convergence increases with the square of
the distance the observers travel north. The formula is
Convergence = (1/2)x(east-west distance at equator) x (distance moved
north)2 / (radius of earth)2
where the formula holds only as long as the two distances are very small
compared to the radius of the earth. This formula can be inverted to
determine the radius of the earth from local measurements of the other
distances in the formula.
3.This same effect of geodesic deviation can be used to detect curvature in the worldines of bodies in spacetime.
(a) The simplest case is the gravitation free Minkowski spacetime. Consider four objects arranged at equal distances apart in a straight line in Minkowski spacetime and initially at rest. Draw a spacetime diagram of their ensuing worldlines. Use the notion of geodesic deviation to conclude that the portion of the spacetime that they are exploring is not curved.
(b) Now imagine that the same four bodies were momentarily at rest above
the surface of a planet and that they all begin to fall towards it, with the
closer bodies falling faster. Use the notion of geodesic deviation to
conclude that the portion of spacetime they are exploring is curved.
For discussion in the recitation.
A. Einstein took a radically new approach to gravity by declaring it to coincide with a curvature of spacetime. However, as we have seen in the lecture, the same thing can be done with Newtonian gravitation theory, so that all its gravitational effects can be associated with a curvature in some parts of spacetime. So what's new with Einstein's proposal?
B. You can take sheet of paper and wrap it into a cylinder, so that its rightmost edge coincides with its leftmost edge. One can do the same thing in imagination with a cubical chunk of Minkowski spacetime to create a very odd, new spacetime. Take the chunk's rightmost edge and declare that it coincides with its leftmost edge. That means that anyone traveling past the surface marking rightmost edge of this space would simply pop back at the surface marking the leftmost edge. Use geodesic deviation to convince yourself that the wrapping up of this spacetime has not changed the flatness of the spacetime.