Assignment 8: Non-Euclidean Geometry

For submission Tuesday February 27/ Wednesday February 28

1. Consider a geometry in which Euclid's 5th postulate is replaced by:

Through any point NO line can be drawn parallel to a given line.

Show that there is at least one triangle in this geometry whose angles sum to more than two right angles.
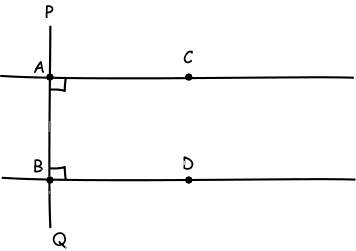
Hint: On a line PQ select two points A and B. Construct lines AC and BD perpendicular to PQ. What happens if AC and BD are extended in both directions?

2.In a Euclidean space, what is
(a) the sum of the angles of any triangle;
(b) the circumference of a circle with radius 10,000 km;
(c) the area of a right angled triangle if the length of the sides enclosing the right angle are both 10,000 km?

3. The geometry of 1. above, suitably treated, is the geometry of the surface of a sphere. The Earth is, to good approximation, a sphere of circumference 40,000 km.
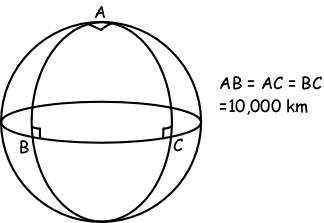
(a) On this sphere, what is the sum of the angles of a triangle all of whose sides are 10,000 km? (An example of such a triangle is shown as triangle ABC. It has one vertex at the North Pole and extends down to the equator.)
(b) What is the circumference of a circle of radius 10,000 km in this surface?
(c) The triangle ABC is a right angled triangle all of whose sides are 10,000 km long. What is its area? (Reminder: The area of the Earth is 509,300,000 sq.km.) Compare your answers in question 2 and 3.

4. If you had before you a two dimensional surface of constant curvature, how could your determine whether the curvature was positive, negative or zero by measuring
(a) the sum of angles of a triangle;
(b) the circumference of a circle of known radius?

5. How could you check whether our three dimensional space has a positive, negative or zero curvature by measuring
(a) the sum of angles of a triangle;
(b) the surface area of a sphere of known radius?

For discussion in the recitation.

A. The discovery of non-Euclidean geometries eventually precipitated a crisis in our understanding of what has to be and what just might be the case. At one extreme are truths of logic, which simply must be true by force of reason alone. At the other mundane factual matters, which may or may not be true. Somewhere in between is a transition. Just where should it come?

Here is a series of propositions that begin with logical truths and bleed off into ordinary empirical propositions. Where should we place the division? How are you deciding this?

If A and B are both true, then A is true.
If one of A or B is true and A is false, then B is true.
For any proposition A, either A is true or A is not true.
1 + 1 = 2
7 + 5 = 12
There are an infinity of prime numbers.
Every circle has one center.
The sum of the angles of a triangle is two right angles.
Every effect has a cause.
Energy is always conserved.
Force equals mass times acceleration.
The earth has one moon.