| HPS 0410 | Einstein for Everyone | Spring 2007 |
Back to main course page
Assignment 3: The Problem of Reciprocity
For submission Tuesday January, 23, Wednesday January 24.
Two inertial observers are in relative motion and each judges the other's rods to have shrunk. While this may seem paradoxical at first, we saw in the Problem of Reciprocity that the aura of paradox is dispelled once we attend to the relativity of simultaneity and the way that judgments of simultaneity figure in the determinations of lengths.
Now consider the clocks carried by each observer. Each observer will judge the other's clock to have slowed. Drawing on the discussion in the Section Relativity of Simultaneity and the Measurement of the Rates of Clocks , we will now review how this can come about without contradiction.
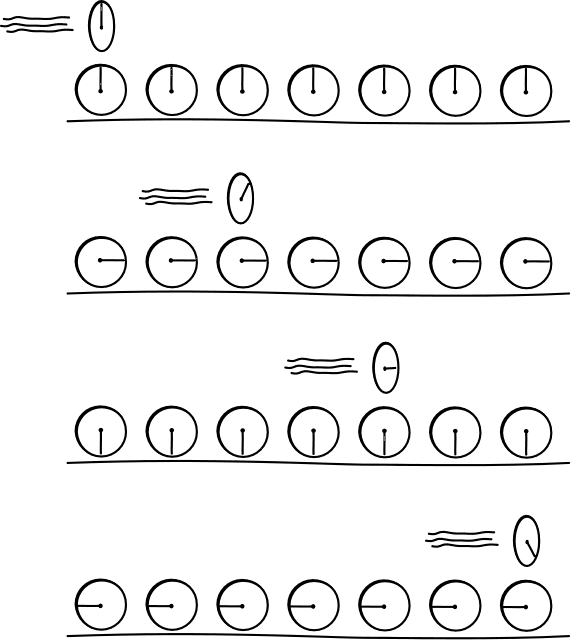
1. If I am standing on a road with a clock and a car carrying another clock speeds past, what procedure can I use to determine the rate of that moving clock?
2. How do judgments of simultaneity figure in the procedure?
3. Assuming you used the procedure associated with the figure below from the lecture, would an observer traveling with the moving clock judge your roadside clocks to be improperly synchronized? If so, which would that observer judge to be set ahead and which behind?
(Hint: This set up is pretty much exactly the one we already looked at in Assignment 2.)
4. What effect would the moving observer judge these mis-settings to have on your judgments? Are they compatible with the moving observer judging your clocks to be running slower?

For discussion in the recitation.
A. Two identical spaceships pass one another in opposite directions at the same speed. The planet observer thinks that they have both shrunk the same amount due to relativistic length contraction. But the observer on Spaceship 1 thinks that Spaceship 2 is shorter than Spaceship 1. And the observer on Spaceship 2 thinks that Spaceship 1 is shorter than Spaceship 2. How is it possible for all of of them to come to such different judgements?
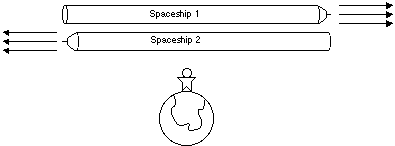
Hint: Relativity of simultaneity...as if you needed it!
B. Do moving rods really contract and moving clocks really slow? Or is all just an illusion brought about by the funny way relativity gets us to synchronize our clocks?
C. When a golfclub strikes a golfball, the ball is accelerated to a higher velocity than that of the club head. Classically, with a heavy club head and a perfectly elastic golfball, the ball can be impelled to twice the speed of the club head. Might a sufficiently robustly constructed club and ball, wielded with sufficient speed, be able to accelerate the ball past the speed of light?
What kinematical effects in special relativity block this means of accelerating something past the speed of light?
What dynamical effects in special relativity block it?