|
John D. Norton
Formal Approaches
to Inductive Inference
|
|
home >> research
>> induction and confirmation: formal approaches |
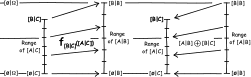 |
The probability calculus is not the universal logic of induction;
there is no such thing. An axiom system disassembles the probability
calculus into distinct notions about induction, which it is urged,
may be invoked independently to tailor a logic of induction to the
problem at hand. The probability calculus fails as the inductive
logic of certain indeterministic systems. |
"Probability Disassembled," British Journal for
the Philosophy of Science, 58 (2007), pp. 141-171. Download.
|
 |
Forming the dual is a familiar operation in logic and mathematics.
Truth is the dual of falsity; and (A or B) is the dual of (A and B).
Here I develop the corresponding notion for additive measures, such
as probability measures. The resulting dual additive measures are
degrees of disbelief and turn out to obey their own peculiar
calculus. An ignorance state is conveniently characterized as one
that is self-dual. |
"Disbelief as the Dual of Belief," International
Studies in the Philosophy of Science, 21(2007), pp. 231-252. Download. |
 |
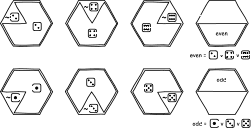
What if, like me, you don't think that the probability calculus is
the One, True Logic of Induction? Then you want to know what other
logics are possible. Here I map out a large class of inductive
logics that originate in the idea that the inductive support B
affords A, that is "[A|B]," is defined in terms of the deductive
relations among propositions. I demonstrate some very general
properties for these logics. In large algebras of propositions, for
example, inductive independence is generic in all of them. A no-go
result forces all the logics to supplement the deductive relations
among propositions with intrinsically inductive structures. |
"Deductively Definable Logics of Induction,"
Journal of Philosophical Logic. 39 (2010),
pp. 617-654. Download.
For a less formal development, see "What
Logics of Induction are There?" in Goodies. |
 |
Non-trivial calculi of inductive inference are shown to be
incomplete. That is, it is impossible for a calculus of inductive
inference to capture all inductive truths in some domain, no matter
how large, without resorting to inductive content drawn from outside
that domain. Hence inductive inference cannot be characterized
merely as inference that conforms with some specified calculus. |
"A Demonstration of the Incompleteness of Calculi
of Inductive Inference" British Journal for the Philosophy of
Science, 70 (2019), pp. 1119–1144.
Download.
"The Ideal of the Completeness of Calculi of Inductive Inference: An
Introductory Guide to its Failure" Draft |
 |
An infinite lottery machines chooses without favor among a
countable infinity of outcomes. This sort of selection creates
well-known problems for probability theory. But is it really
physically possible to construct such a machine?. |
"How to Build an Infinite Lottery Machine" 8 (2018),
pp. 71-95.
(with Alexander R. Pruss) Correction to John D. Norton “How to Build
an Infinite Lottery Machine, ” European Journal for Philosophy
of Science. 8 (2018), pp. 143-44.
Download. |
|
All efforts to design an infinite lottery machine using ordinary
probabilistic randomizers fail. This failure is not a result of a
lack of imagination in design. It is assured by a familiar problem
in set theory: we know no way to construct probabilistically
nonmeasurable sets. |
"How NOT to Build an Infinite Lottery Machine." Studies
in History and Philosophy of Science. 82(2020),
pp. 1-8. Download. |

|
Matt Parker and I disagree on whether a multiple of four is less
likely than an even number in a drawing from an infinite lottery.
|
"An Infinite Lottery Paradox" Axiomathes
32, supplement issue 1 (2022), (Special Issue Epistemologia
2022), pp. 1-6. Download.
|
|
Here is an illustration of how it is possible in a principled way
to devise a strict weakening of the probability calculus that is
non-additive and not prone to the Bayesian's notorious problem of
the priors. It represents an interesting technical exercise, but I
regard it as superceded by the analyses of the later papers above. |
"The Theory of Random Propositions," Erkenntnis,
41, 1994, pp. 325-352.
|
|
|






