|
John D. Norton
Critique of Bayesiansim
Induction and Confirmation
|
|
home >> research
>> induction and confirmation: critique of bayesianism |
 |
Non-trivial calculi of inductive inference are shown to be
incomplete. That is, it is impossible for a calculus of inductive
inference to capture all inductive truths in some domain, no matter
how large, without resorting to inductive content drawn from outside
that domain. Hence inductive inference cannot be characterized
merely as inference that conforms with some specified calculus. |
"A Demonstration of the Incompleteness of Calculi
of Inductive Inference," British Journal for the Philosophy of
Science, 70 (2019), pp. 1119–1144.
Download
"The Ideal of the Completeness of Calculi of Inductive Inference: An
Introductory Guide to its Failure" Draft |
 |
A probabilistic logic of induction is unable to separate cleanly
neutral support from disfavoring evidence (or ignorance from
disbelief). Thus, the use of probabilistic representations may
introduce spurious results stemming from its expressive inadequacy.
That such spurious results arise in the Bayesian "doomsday argument"
is shown by a reanalysis that employs fragments of inductive logic
able to represent evidential neutrality. Further, the improper
introduction of inductive probabilities is illustrated with the
"self-sampling assumption." |
"Cosmic Confusions: Not Supporting versus Supporting
Not-" Philosophy of Science. 77 (2010),
pp. 501-23. Download. |
 |
While Bayesian analysis has enjoyed notable success with many
particular problems of inductive inference, it is not the one true
and universal logic of induction. I review why the Bayesian approach
fails to provide this universal logic of induction. Some of the
reasons arise at the global level through the existence of competing
systems of inductive logic. Others emerge through an examination of
the individual assumptions that, when combined, form the Bayesian
system: that there is a real valued magnitude that expresses
evidential support, that it is additive and that its treatment of
logical conjunction is such that Bayes' theorem ensues. |
"Challenges to Bayesian Confirmation Theory," Philosophy
of Statistic, Vol. 7: Handbook of the Philosophy of Science.
Prasanta S. Bandyopadhyay and Malcolm R. Forster (eds.) Elsevier,
2011. Download. |
 |
The probability calculus is not the universal logic of induction;
there is no such thing. An axiom system disassembles the probability
calculus into distinct notions about induction, which it is urged,
may be invoked independently to tailor a logic of induction to the
problem at hand. The probability calculus fails as the inductive
logic of certain indeterministic systems. |
"Probability Disassembled," British Journal for
the Philosophy of Science, 58 (2007), pp. 141-171. Download.
|

|
In a material theory of induction, inductive inferences are
warranted by facts that prevail locally. This approach, it is urged,
is preferable to formal theories of induction in which the good
inductive inferences are delineated as those conforming to some
universal schema. An inductive inference problem concerning
indeterministic, non-probabilistic systems in physics is posed and
it is argued that Bayesians cannot responsibly analyze it, thereby
demonstrating that the probability calculus is not the universal
logic of induction. |
"There are No Universal Rules for Induction,"Philosophy
of Science, 77 (2010) pp. 765-77. Download
|
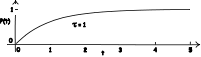
|
A simple indeterministic system is displayed and it is urged that
we cannot responsibly infer inductively over it if we presume that
the probability calculus is the appropriate logic of induction. The
example illustrates the general thesis of a material theory of
induction, that the logic appropriate to a particular domain is
determined by the facts that prevail there. |
"Induction without Probabilities." Download.
See also "Induction without
Probabilities" in Goodies.
|
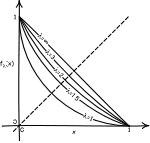
|
The epistemic state of complete ignorance cannot be a probability
distribution. The instruments that characterize it are innocuous
platitudes of evidence: the principle of indifference and certain
invariance conditions. However the literature has misdiagnosed these
instruments as defective since these instruments rule out the
representation of complete ignorance by probability distributions. |
"Ignorance and Indifference." Philosophy of
Science, 75 (2008), pp. 45-68. Download.
|
|
|