John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh
Pittsburgh PA 15260.
Homepage: www.pitt.edu/~jdnorton
This page is available at www.pitt.edu/~jdnorton/goodies
While the literature in philosophy of physics is huge, it turns out that much
of it is devoted to just three general problems.
They arise in the pair-wise interactions of the three main elements of modern
physics:
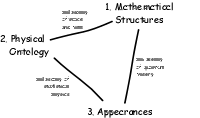
1. Mathematical structures
2. Physical ontology
3. Appearances
Each pair happens to have a strong association with the philosophical
problems that arise in one particular branch of philosophy of physics. The
situation is portrayed in a figure.

Generally speaking, in a physical theory, distinct mathematical structures would be presumed to represent distinct elements of the physical ontology. That presumption can fail in the special case in which simple mathematical transformations relate the two structures. There is no rule that asserts that structures so related must represent the same ontology. The decision as to whether they do is a physical matter that must be settled by physical argumentation that often proves quite delicate.
The two general ways in which
the mathematical structures may be related. They are by symmetry
transformations and gauge transformations. Two structures related by the
first are more closely related and thus tend most often to be judged
equivalent in the physical ontology..
A symmetry
transformation leaves the mathematical structure unchanged, e.g. a
translation or a rotation in a Euclidean space. This is the strongest form of
interrelation. A symmetry transformation expresses a homogeneity of space or
a relativity principle. e.g. The Lorentz transformation is a symmetry of a
Minkowski spacetime. In the case of a symmetry transformation, we can only
say that the original and transformed structures represent something
different in the ontology by calling on something outside what is described
by the mathematical structures of the theory. e.g. In a Minkowski spacetime
free of all other material structures, a Lorentz transformation can be
construed as shifting one "God's eye" observer's frame to another in
relative motion.
A gauge transformation alters the mathematical structure but in a way for which we have some reason to believe that the physical ontology represented is unchanged. The simplest example is a real valued field in Euclidean space representing a Newtonian gravitational field. Since differences in potential only have physical meaning, we can always add a real constant to the field without changing the physical ontology, although the numerical value of the potential field will be changed throughout. This addition is a gauge transformation. The principal challenge with a gauge transformation is finding grounds for judging that the distinct mathematical structures represent the same thing physically. Two sorts of grounds have been used: verificationism--there is no observable difference between what the two structures represent; indeterminism--if we insist the two structures represent distinct physical ontologies, we gratuitiously visit indeterminism of the theory. These grounds were first thoroughly explored in the context of discussion of the "hole argument" of general relativity.
The most familiar example of a
symmetry transformation is the transformation between inertial frames of
reference in special relativity. The next most familiar example of these
sorts of transformations is the general coordinate transformations of general
relativity, licensed by its general covariance. An issue that is still
debated is whether these transformations are best understood as symmetry
transformations or gauge transformations.
There is an interesting inversion of the general problem with the existence of unitarily inequivalent representations of the commutation relations in algebraic quantum field theory. These are structures that are not intertransformable, but plausibly should somehow represent the same ontology. Or should they?

Quantum theory is our most successful theory of microscopic phenomena. Its mathematical structure is based on the Schroedinger equation. One of the fundamental properties of this equation is its linearity. That just means that if we have any two solutions of the equation, then their sum is also a solution. The sum is known as the superposition of the two original solutions. For examaple, if a radioactive atom decaying or not decaying solves Shroedinger's equation, then the superposition of the atom both decaying and not is also a solution.
This sort of superposition routinely arises microscopically. Since Schroedinger's equation holds equally for small and big systems, unless something intervenes, we should expect these superpositions for macroscopic systems as well. If the radioactive atom's decay triggers a mechanism that kills a cat, we should expect the superposition of decayed and undecayed atom to be coupled to a superposition of dead and live cat. This is the Schroedinger's cat thought experiment. Of course no such superpositions are seen macroscopically, in the appearances.
The measurement
problem is the label given to the problem of dealing with our failure to see superpositions in ordinary appearances.
In traditional solutions of the problem, two types of time development are
distinguished: Schroedinger evolution (spreading of the wave packet that
admits superposition) and measurement (collapse of the wave packet). The
second happens to macroscopic objects like cats in superpositions, when we
ascertain their state: they collapse to either the live or dead state.
Unfortunately we do not have precise rules to decide when one or the other
happens. Rather we have pretty good rules of thumb that work well for
practical applications of the theory. If a quantum system interacts with
something big, it collapses; if it interacts with one or two other particles,
or none at all, it spreads. But how are we to handle the intermediate cases?
No-collapse theories try to deal with the problem by proposing that
superposition does happen at the macroscopic level--there really are two
cats, one alive and one dead. Because of our presence in the world, we are
part of that superposition and that makes us aware of only one part of it.
These are the "many world" interpretations of quantum theory.
I have characterized the measurement problem as arising from a tension between the mathematical formalism of quantum theory and the appearances rather than from a tension between the physical ontology and the formalism. The reason is that the precise physical ontology of quantum theory remains unclear. What is secure, at least on the microscopic level, is the mathematics of quantum theory, most notably the Schroedinger equation. It is that mathematics, rather than definite ideas on ontology, that lead us to expect superpositions in the small and the big.
That the ontology of quantum theory is unclear is a second
foundational problem that lies on the 1-2 side of the triangle above. Usually the association of ontology with mathematical
structures is not so difficult to achieve. Invariant line elements in a
metrical space are associated with physical distances in the physical space.
Or the magnetic field strength vector field of electrodynamics is associated
with the magnetic field supported by a magnet. For quantum theory the problem
of deciding which is the correct association has proven remarkably
recalcitrant.
Interpretations of quantum theory is the general term given to the problem of identifying the physical ontology associated with the mathematical structures of quantum theory. It is enmeshed with the measurement problem, which greatly complicates any decision. The Schroedinger wave of a charged particle was initially hoped to be some sort of charge distribution; and then perhaps a wave of probability or potentiality, whatever that might mean; and most recently the theory is somehow about "quantum information." The most refractory problems have been presented by superpositions and entangled states. The problems of the latter were brought to prominence in the Einstein-Podolsky-Rosen paper of 1935 and developed later by Bell. The concensus arising from this problem is of an unavoidable non-locality or non-separability in the theory's physical ontology. The problems of the former (superpositions) were emphasized by Schroedinger's "cat" paper also of 1935.

In this problem, we face some sort of systematic mismatch between the physical ontology and
the appearances. Two important instances arise in statistical physics.
The asymmetry of time. Excepting weak interactions, all our microphysics is time reversible. The appearances of the macroscopic world are strongly directed in time, distinguishing past from future. How can this asymmetry arise from the microphysics?
Phase transitions. The interactions of microphysics are represented by differential equations that admit no discontinuities. The appearance of thermal systems is characterized by discontinuous transformations--phase transitions, such as between solid and gaseous state. How can the appearance of discontinuity arise from a continuous ontololgy?
These two problems are specific manifestations of a more general problem in statistical physics: can we say that thermodynamics recovered from appearances stands in a reduction relation with the microphysics of molecules and other minutiae that populate our deeper ontology? Getting a clear answer to that question has proven hard. Part of the problem is to determine just what sense of reduction is required. Is it an ontological sense in which water or perhaps facts about water are nothing other than water molecules or perhaps facts about water molecules? Few doubt that this ontological sense obtains. Or is it a "Nagel" style reduction in which the thermodynamic facts about water (or some approximate surrogate) are to be deduced from the theory of water molecules? This latter sort of reduction has failed quite often. Or are we to seek some as yet unexplicated notion that lies in between?
This general problem can arise in many other contexts. For example, Einstein in 1905 worried about how to reconcile the presence of a preferred ether state of rest in the fundamental ontology of then current electrodynamics with appearances that conformed to the principle of relativity. Some versions of no-collapse theories of quantum mechanics must explain how quantities appear to have sharp values when their version of quantum mechanics says that they really do not (see above).
November 30, 2006