John D. Norton
Department of History and Philosophy of Science, University of Pittsburgh
Pittsburgh PA 15260. Homepage: www.pitt.edu/~jdnorton
This page (with animated figures) is available at www.pitt.edu/~jdnorton/goodies
It is routinely assumed that Einstein discovered the relativity of simultaneity by thinking about how clocks can be synchronized by light signals, much in accord with the analysis he gave in his 1905 special relativity paper. Yet that is just supposition. We have no real evidence that it actually happened this way. In later recollections, Einstein stressed the importance of several thought experiments in the thinking that led up to the final theory. They include his chasing a light beam thought experiment and his magnet and conductor thought experiment. They do not include thought experiments on clocks and their synchronization. My goal here is to show that other pathways to the relativity of simultaneity are quite plausible. In several places Einstein stressed the importance in his discovery of special relativity of stellar aberration and Fizeau's measurement of the speed of light in moving water. The results can be seen as direct observational expressions of the relativity of simultaneity, if one knows how to read them. I will suggest that, thanks to his knowledge of Lorentz's 1895 Versuch, Einstein did know how to read them, and that it is quite possible that these observations first led Einstein to the relativity of simultaneity.
Download this document as a pdf for printing with still figures.
For more details, including references to the literature, see John D. Norton, "Einstein's Investigations of Galilean Covariant Electrodynamics prior to 1905," Archive for History of Exact Sciences, 59 (2004), pp. 45-105. (Download) and John D. Norton, "Einstein's Special Theory of Relativity and the Problems in the Electrodynamics of Moving Bodies that Led him to it." in Cambridge Companion to Einstein, M. Janssen and C. Lehner, eds., Cambridge University Press, forthcoming. (Download)
After seven and more years of toil, Einstein made the breakthrough that brought him his special theory of relativity. Some five to six weeks were then needed to complete his famous 1905 paper, "On the Electrodynamics of Moving Bodies." The breakthrough was his recognition of the relativity of simultaneity: judgments of the simultaneity of events will vary according to the state of motion of the observer. As a reflection of its importance, Einstein later simply talked of the discovery as "The Step."
This recognition proved to be key to the new theory. It enabled him to dissolve the paradoxes that the theory might otherwise bring. How is it possible that an observer chasing rapidly after a propagating light wave judges no slowing down of the wave? The rapidly moving observer has judgments of simultaneity reconfigured in exactly the way needed to undo any effect of the observer's motion on the measured speed of light.
Einstein's analysis of simultaneity is provided in the first section of the 1905 special relativity paper. It establishes the relativity of simultaneity by investigating the behavior of clocks synchronized by light signals using natural rules. The analysis is the most celebrated conceptual analysis of 20th century science and has become a model for theorizing both inside and outside physics.
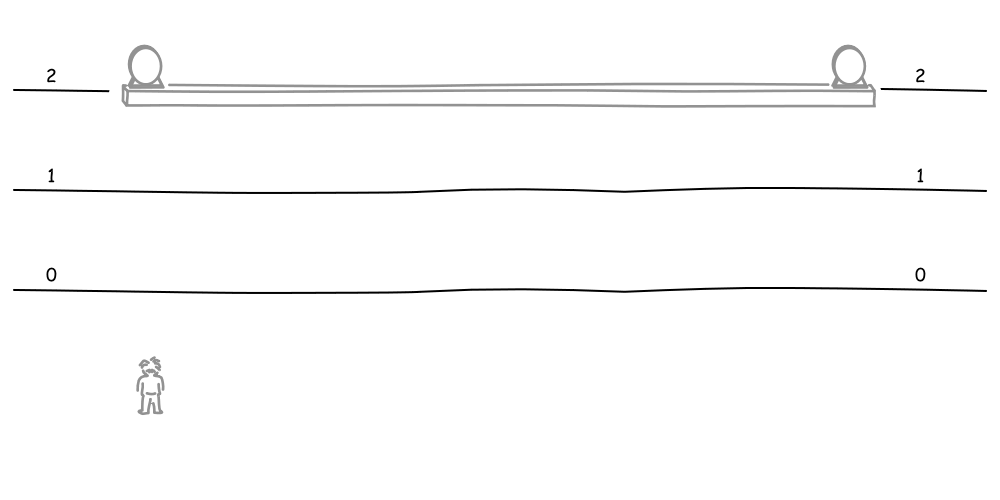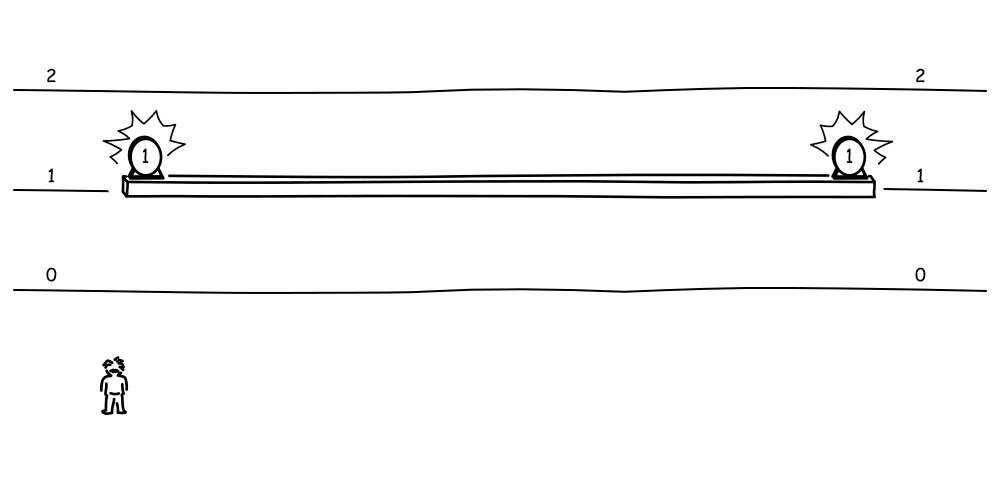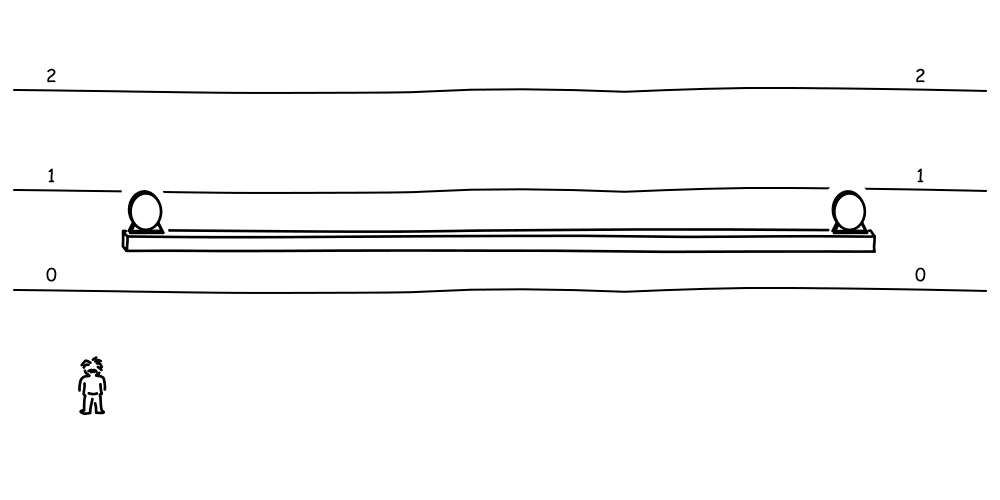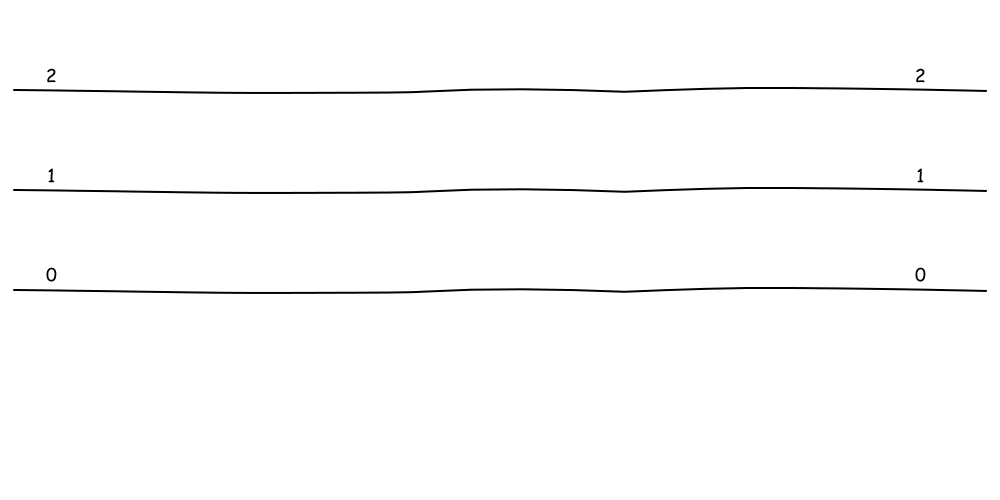
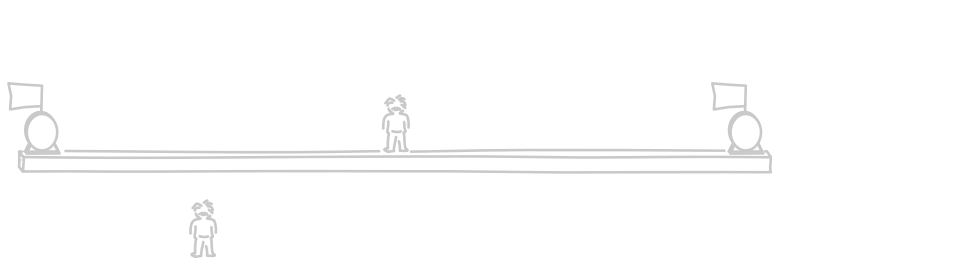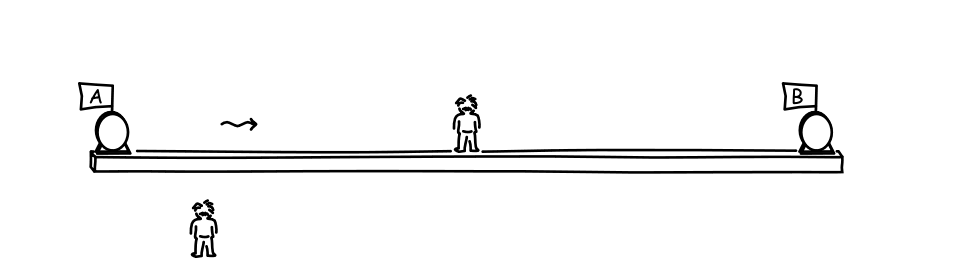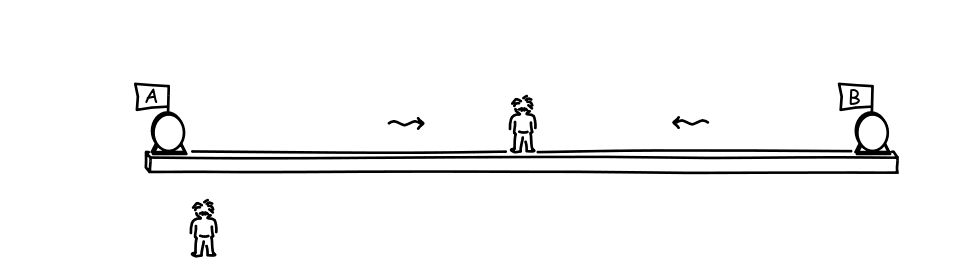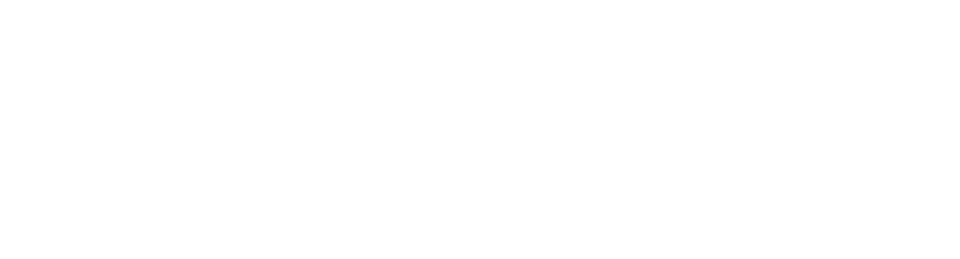
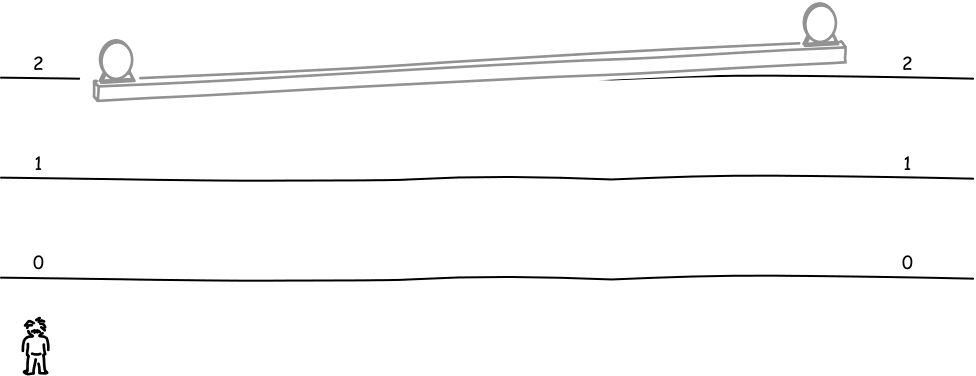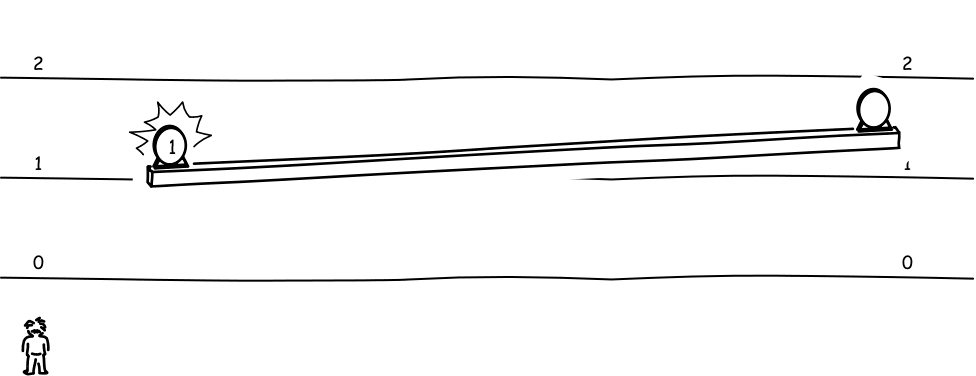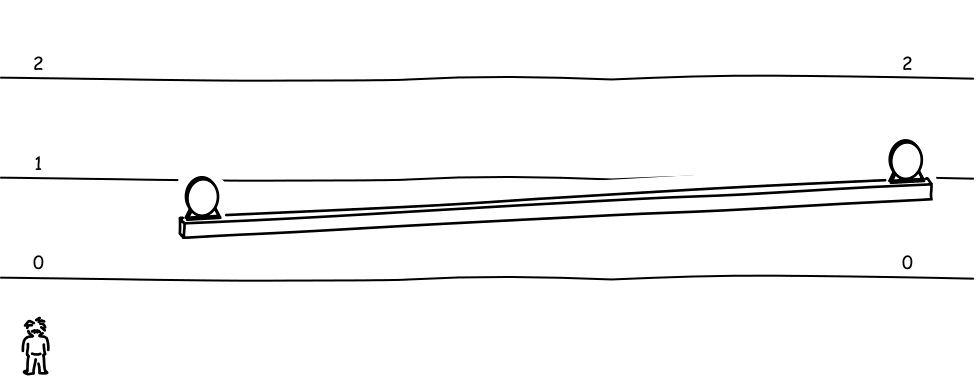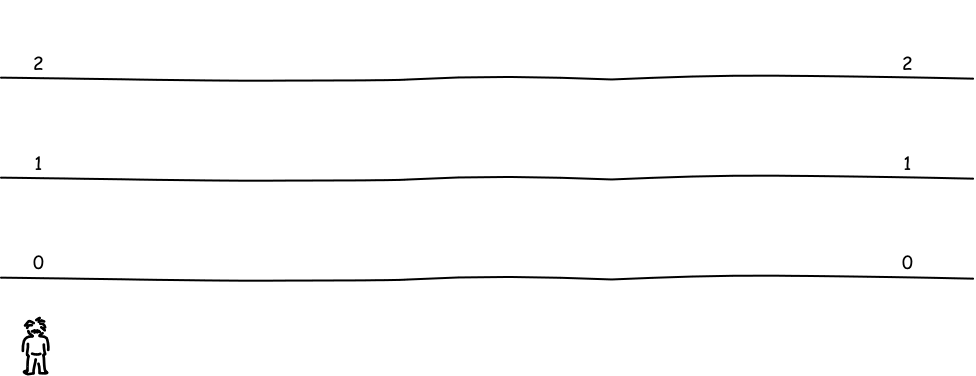
Here's a simplified version of the analysis. We have two clocks--the "A" clock and the "B" clock--widely separated in space. Our goal is to check whether they are properly synchronized. To do this, we arrange for the clocks each to flash when they read 0 time. An observer located midway between the two clocks waits for the resulting light signals to arrive. If the signals arrive at the same moment, as they do in the figure below. Then the observer at rest with respect to the clocks will judge the flashes at clocks A and B to be simultaneous events and the two clocks to be properly synchronized.
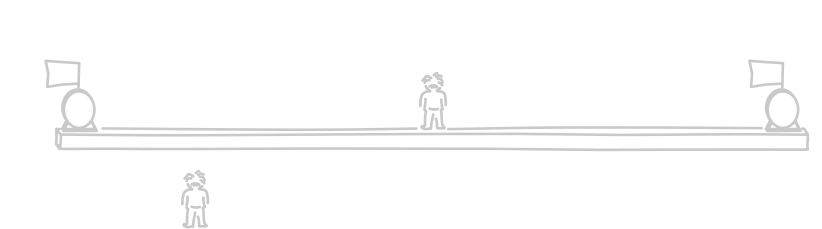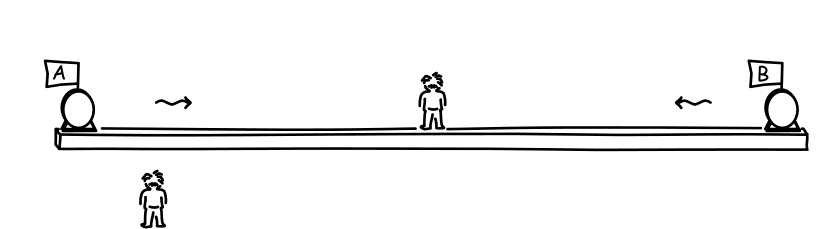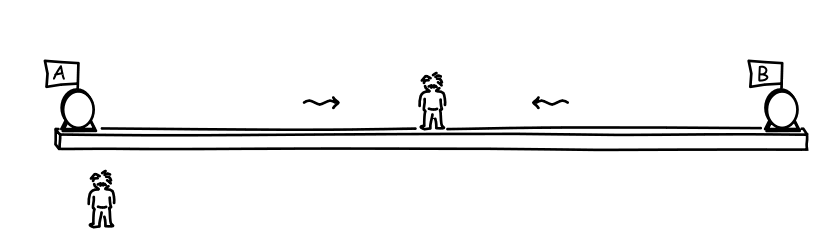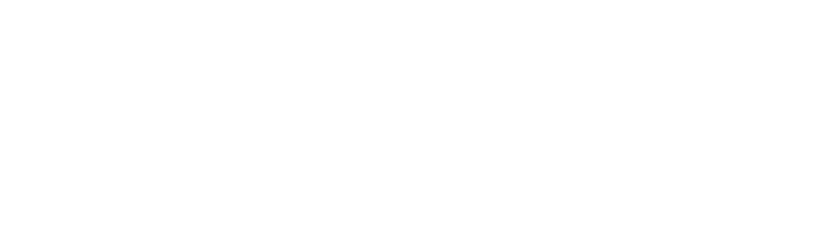
Now imagine that there is a second observer who moves uniformly with respect to the clocks, as shown in the figure above at the bottom left. How will that observer judge the synchrony test? According to the second observer, both clocks, the first observer and the platform that holds them will all be moving uniformly as a whole in the direction of the B clock.
So, as far as the second observer is concerned, the light signal traveling from the A clock will have to traverse a greater distance to arrive at the midpoint of the platform, for the midpoint of the platform is fleeing from it. And the light signal from the B clock will have to traverse a lesser distance, since the midpoint of the platform is rushing towards it.
Yet the two light signals will arrive at the moving midpoint at the same moment. How is that possible? The signal from the A clock has greater distance to travel, so perhaps it just traveled faster? We must rule out that possibility. The special theory of relativity is based on the light postulate, which asserts that all inertially moving observers judge the same speed for light. So both signals are traveling at the same speed for the second observer (as well as the first).
The two light signals can only arrive at the moving midpoint at the same moment if the flash at the A clock happened earlier, thus giving the signal from the A clock more time to cover the greater distance. And the flash at the B clock happened later, so it needed less time to cover the distance to moving midpoint.
Here we see the relativity of simultaneity. The first observer, at rest with respect to the clocks, judges the two flashes to be simultaneous and the two clocks to be properly synchronized. The second observer judges the A flash to happen first and the A clock to be set ahead of the B clock. More generally, the times of events must accord with the readings of clocks properly synchronized by the above procedure. Since that procedure yields different judgments of simultaneity for different frames of reference, there is no longer an absolute fact as to whether two events are simultaneous; that judgment can vary from frame to frame.
We can immediately see how the relativity of simultaneity dissolves paradoxes. It might seem impossible that both of the observers could judge light to travel at the same speed. To see that it can happen, recall that judgments of the speed of light must conform to the measurement of the time it takes a light signal to traverse some interval of space. These measurments are made by clocks at the start and end of that interval and it is essential that the clocks be synchronized.
If the two observers making these measurements use sets of clocks that are synchronized differently, then it is no longer so clear how their results will compare. Indeed it might be possible for them to adopt different protocols for synchronizing their clocks, both of which are carefully selected exactly to assure that both observers measure the same speed for light. Only a little reflection shows that using Einstein's method of synchronizing clocks is exactly such a protocol. In effect it is a prescription for synchronizing clocks that assures that all observers end up with the same speed for light.
Someone is going to ask, so here goes. Does this mean that Einstein's light postulate is simply a stipulation enforced by the protocol for synchronizing clocks? That is, is the light postulate just a factually empty assertion? No. Definitions often presume certain factual conditions and these conditions may be non-trivial. For example, we may define the age of the universe as the time elapsed since the big bang. But that assumes there was a big bang. Similarly Einstein's definition of simultaneity rests upon non-trivial, factual assumptions. It assumes that the synchronization procedure is always applicable, no matter what the speeds of the clocks A and B happen to be. Indeed this must be the case on pain of violating the principle of relativity. For if it failed then we would have distinguished preferred motions, that is, those select motions for which the definition is applicable. That the definition must be applicable to all uniformly moving clocks means that the clocks cannot move so that they outrun light. For if that were to happen, the light signals emitted by the clocks could not be used to synchronize them by Einstein's definition. That factual presumption of the definition already indicates that we are outside the classical realm, for in the classical realm no property of space and time precludes idealized clocks from outrunning light. Of course Einstein's definition could be used in the classical context if light conformed to an emission theory, in which the velocity of the light emitter is added vectorially to the velocity of the light. In that case, Einstein's definition would return the familiar absolute simultaneity of classical theory. But an emission theory is precluded in special relativity by the part of the light postulate that asserts that the velocity of light is independent of the velocity of the emitter. This part of the light postulate is independent of any judgments of simultaneity. To see this independence, imagine that a resting and a moving light emitter momentarily coincide when they each emit a light flash in the same direction. This part of the light postulate entails that the flashes remain coincident as they propagate. This coincidence can be affirmed without making judgments of simultaneity. For completeness, I note that I set aside issues raised in the discussion of the conventionality of simultaneity. I simply presume that a synchrony rule will be applied symmetrically in space.
The relativity of simultaneity permeates special relativity. It can lead to unexpected behavior in any quantity that requires synchronized clocks for its measurement. The most familiar example is the length of a moving body, since that length is given by the distance between the object's endpoint at the same moment in time.
A less familiar example is the orientation of bodies in motion. As we shall see, if observers change their state of motion in some direction, bodies moving transverse to that direction will be rotated.
The figure below shows a rod moving vertically, passing over horizontal lines marked "1," "2" and "3". The rod is oriented parallel to those lines. The judgment of that orientation includes a judgment of simultaneity. For it amounts to saying that both ends of the rod pass each horizontal line at the same moment. So when each end passes the line marked "1," the synchronized clocks at either end read the same time "1".

Now consider how this same motion will be judged by the observer shown above, who moves horizontally. That observer will not judge the two clocks on either end of the rod to be properly synchronized. Indeed using the earlier analysis, we know that observer will judge the clock on the left (corresponding to the A clock above) to be set earlier than that one on the right.
Therefore the event of the left end of the rod passing the line marked "1," will be judged by that observer to have happened earlier than the passing of the right end of the rod. The outcome is that this horizontally moving observer will regard to the rod to have been rotated slightly.
This rotation is a direct result of the relativity of simultaneity; it expresses the relativity of simultaneity. The illustration shows the effect for a rod equipped with clocks. The argument leading to the effect is sufficiently general to work for any other object that moves vertically. That includes a propagating wavefront, a fact that will be become important shortly.
I will argue that it is possible that Einstein hit upon the relativity of simultaneity when he recognized that two experimental results are each direct observational manifestations of the relativity of simultaneity. They are Fizeau's measurement of the speed of light in moving water and stellar aberration . Here I will develop just the case of stellar aberration. I propose that a similar development is also possible for Fizeau's measurement. However, I will forgo describing it here since it is harder to put it in the simple, pictorial form possible for stellar aberration.
Stellar aberration was discovered by Bradley in 1728 when he found that the apparent position of a distant star was altered in consort with the earth's motion around the sun.
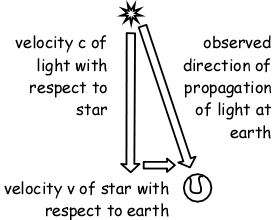
The rule for computing the alteration is simple. One takes the velocity of the light with respect to the star; and adds vectorially to it the velocity of the star with respect to the earth. The direction of the resulting vector is the apparent direction of the starlight as measured on earth. The "angle of aberration" is the difference between the true and apparent angular position of the star.
The figure at left shows the application of the rule for the case in which the angle of aberration is at its maximum: the case of the direction of the earth's motion perpendicular to the direction of the starlight.
In this case, if the speed of the earth is v and speed of light c, it is immediately apparent from the figure that the angle of aberration is v/c radians, where it is important for this result that v is very much smaller than c.
Since all the velocities mentioned in the rule are relative velocities, the rule conforms to the principle of relativity. This is not so surprising as long as we work within a Newtonian corpuscular theory of light. Then we just treat light like little particles in Newtonian dynamics and the effect is entirely familiar. It is just what car drivers experience if they drive through a vertically falling shower of rain. The effect of the car's motion is to make the rainfall appear to be directed toward to windscreen from the perspective of the car driver. Indeed the angle of aberration for the rainfall could be computed by the above rule.
The above rule for stellar aberration conforms to the principle of relativity. And that seems just fine if we think of light as little, Newtonian corpuscles. But what happens if we analyze stellar aberration in the context of a wave theory of light, such as Maxwell's electromagnetic theory of light? That theory, as developed in the nineteenth century, depended on a preferred ether state of rest with respect to which light propagated at the universal velocity c. Will the effect still arise? Will it still conform to the principle of relativity?
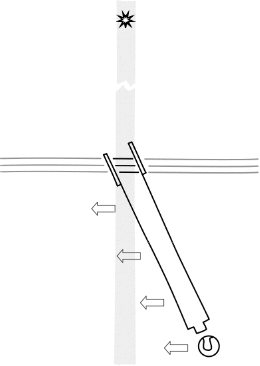
To begin, let us take the easy case. If the star is at rest in the ether and the earth moves, then we recover the effect of aberration by a widely known analysis depicted in the figure below. It takes the case of a star positioned perpendicular to the motion of the earth. If the telescope were pointed directly at the star, starlight entering the end of the telescope would be unable to pass its full length. Since the telescope tube is moving perpendicular to the direction of propagation of the light, the trailing wall of the telescope would move into the path of the light and stop it reaching the eyepiece.
The expedient that makes it possible for the light to reach the eyepiece is to tilt the telescope in the direction of motion of the earth. Then--as the figure shows--the trailing wall never intercepts the light scooped up by the telescope opening as the telescope moves across the path of light propagation. The starlight propagates to the eyepiece.

The familiar analogy is to a tall, upwardly pointing hat used to catch rain in a vertical rain-shower by a runner running through it. The hat must be tilted if the rain is to pass through the opening of the hat to wet the bottom. It turns out the above rule for computing the aberration angle gives exactly the angle through which the telescope tube must be tilted to ensure that the starlight passes through to the eyepiece.
Note that the star is very far away from the earth--something the figure cannot show directly. When the starlight leaves the star, it is an expanding spherical shell. By the time it reaches the earth, we sample such a tiny portion of the spherical shell with our telescopes that the waveforms are effectively (flat) plane waves.
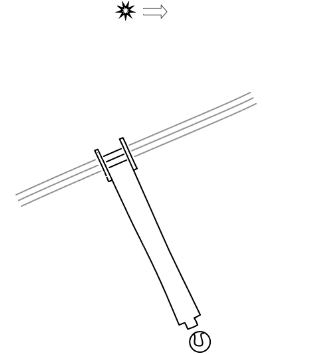
We can quickly see that this full account of aberration will not conform to the principle of relativity. And we should not expect it to, for the account arises in a theory dependent on an ether state of rest. To see the failure, we need merely transform our point of view from the distant star to the earth. So now we treat the earth as at rest and the star moving.
The ordinary rules of Newtonian physics tell us how to transform the view point. The earth will be at rest and the star will be moving in the opposite direction. And--most importantly--the vertically propagating wavefronts of the starlight will still propagate vertically. The result is that the telescope is now pointed in the wrong direction for the starlight to propagate the full length of the telescope tube, as the figure below shows. The telescope tube would have to be pointed directly at the true position of the star if the starlight is to pass.
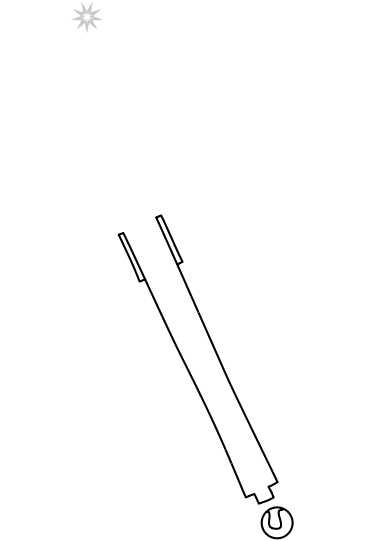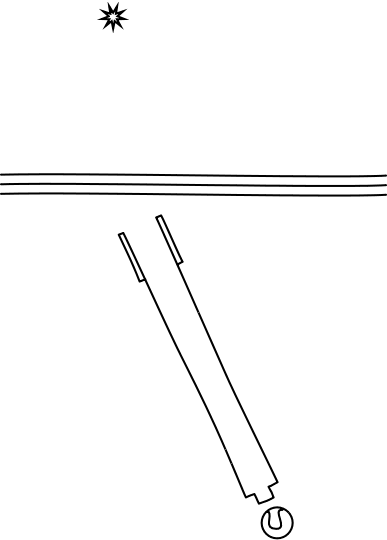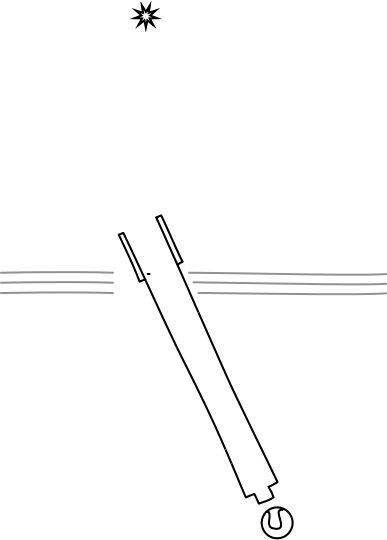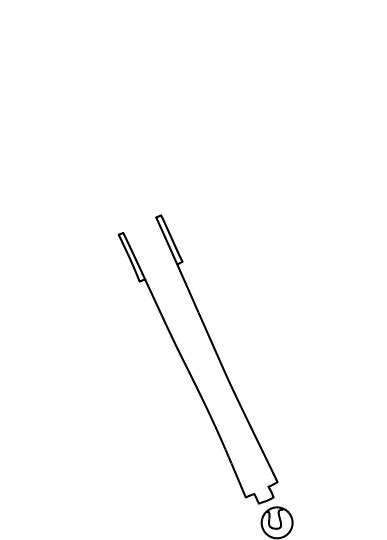
One might be tempted to conclude from the above analysis that stellar aberration gives us a simple way of determining whether we are at rest or moving in the ether of Maxwell's electromagnetic theory of light. If we are on a moving earth, we have stellar aberration. If we are on an earth at rest in the ether, we do not. The analysis does not show that. All it shows is that Maxwell's theory can be applied properly only in one frame of reference, the ether frame of reference. Unlike Newton's mechanics it does not work equally well in all inertial frames of reference. So, what would happen, according to Maxwell's electrodynamics, if the star moves in the ether and the earth is at rest?
One of the great achievements of H. A. Lorentz' celebrated Versuch of 1895 was to answer this last question. He showed that stellar aberration will arise in Maxwell's theory and in such a way that the principle of relativity would be respected, in so far as anything observable was concerned. Maxwell's theory does depend, he urged, on a single preferred ether state of rest. But nothing in what is observable about stellar aberration can reveal that state of rest.
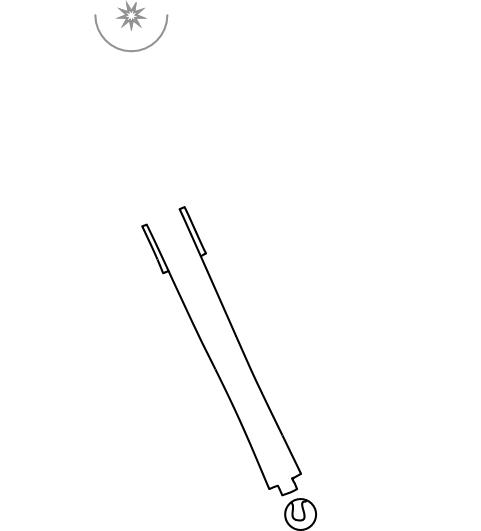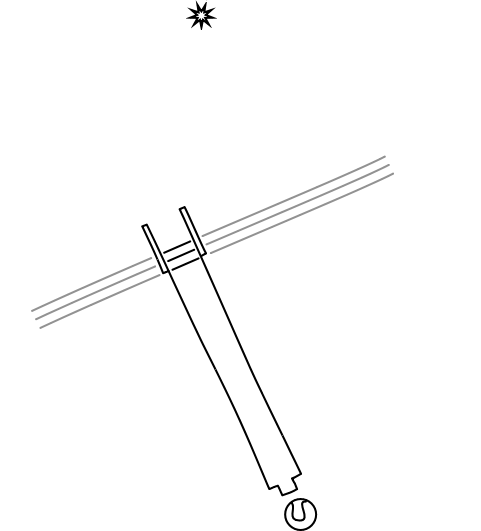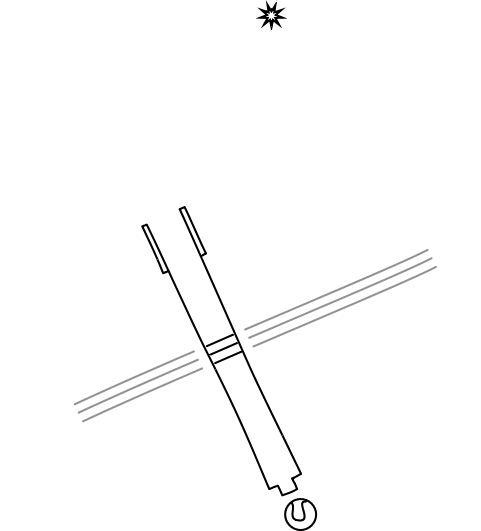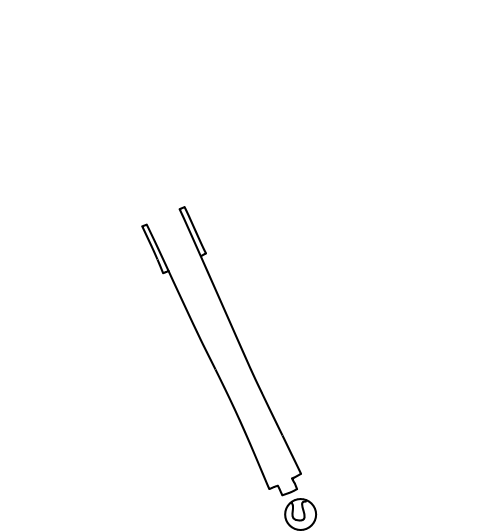
To demonstrate this broad conclusion, at least for the case of stellar aberration, Lorentz considered a second case. He imagined that the earth is at rest in the ether and the star moves, with everything else otherwise the same. He found that, for this case, Maxwell's electrodynamics predicts exactly the same effect as when the earth moves in the ether and star is at rest. In both there is an angle of aberration of v/c radians, with v very much smaller than c, as before. In short, Maxwell's electrodynamic theory of light is dependent on an ether with a preferred state of rest, so it violates the principle of relativity. But as far as the observable of stellar aberration is concerned, that preferred state of rest is invisible. Whether the star or earth is set to rest in the ether, the same observable aberration angle is recovered.
What turns out to be especially interesting is not just this result, but how it was calculated. Lorentz could have set up from scratch the system of the earth at rest in the ether and the light emitting star in motion and solved Maxwell's equations for it. But that would have been a long and arduous calculation. What Lorentz came up with was an ingenious mathematical device, his theorem of corresponding states, which allowed him to arrive at the result with minimal effort.
The theorem did this because it licensed him to take an existing solution of Maxwell's equations and generate new solutions from it by the application of some simple transformation rules. The rules look something like rules that take the original system and set them into uniform motion. However the system set in motion is distorted in odd ways. Those distortions simply had to be accepted, however, since they were needed if the resulting system was to be a solution of Maxwell's equation. In this instance, Lorentz took the original case above of the light emitting star at rest in the ether and the moving earth. Setting it into motion as a whole in just the right way, he generated a new, slightly distorted solution in which the star moved in the ether and the earth was at rest.
The key to the theory was his set of transformation equations, which Lorentz could apply to known solutions to generate new ones. As indicated, these transformations would allow him to switch motion and rest in the ether for the star and earth. (Those who already know how this story finishes will recognize the transformation as what we now call the Lorentz transformation with velocity v, the velocity of the earth.) But what of the distortions? The most significant was associated with Lorentz's notion of "local time". According to it, the new solution is generated from the old by assembling parts of the old solution at different times into a new solution at one time. For the case of v very much smaller than c, the state at time t in the new solution is assembled from the states at times t - (v/c2)x, where x is the spatial coordinate of the direction of the transformation.
The effect of this transformation is a dislocation in the timing of processes. Take the case of a propagating plane wave. A transformation whose velocity is transverse to the direction of propagation of the wave has the effect of rotating the wave front. For v very much smaller than c, the rotation turns out to be just the angle v/c radians. This effect gives the aberration angle of v/c radians.
The similarity of Lorentz' work to Einstein's is very apparent. Lorentz' local time is just like Einstein's notion of the relativity of simultaneity. Indeed they use the same formulae. In both, a transverse transformation of velocity engenders a rotation in a moving body. However they have very different physical interpretations. For Einstein, the relativity of simultaneity betokens an unrecognized physical fact about time. For Lorentz local time is just a mathematical trick that greatly eased the computational burden of finding new solutions of Maxwell's equations.
The obvious questions are these. Did Einstein know of Lorentz's analysis? And did that knowledge somehow figure in his discovery of the relativity of simultaneity? We can answer the first question affirmatively. Einstein reported in many places that he had read Lorentz's Versuch prior to his discovery of special relativity. He also recalled the importance of Fizeau's experiment and stellar aberration specifically. He wrote:
"... Lorentz's path breaking investigation on the electrodynamics of moving bodies (1895), which I knew before the establishment of the special theory of relativity. ...
My direct path to the sp. th. rel. was mainly determined by the conviction that the electromotive force induced in a conductor moving in a magnetic field is nothing other than an electric field. But the results of Fizeau's experiment and phenomenon of aberration also guided me."
Einstein, 1952 , In Memory of Albert A. Michelson...
"... the experimental results which had influenced him most were the observations of stellar aberration and Fizeau's measurements on the speed of light in moving water..."
Einstein reported by Shankland, 1950.
"Prof. Einstein volunteered a rather strong statement that he had been more influenced by the Fizeau experiment on the effect of moving water on the speed of light, and by astronomical aberration, especially Airy's observation with a water filled telescope, than by the Michelson-Morley experiment."
Einstein reported by Shankland, 1950-54.
"...I had the chance to read Lorentz's monograph of 1895. There, Lorentz dealt with the problems of electrodynamics and was able to solve them completely in the first approximation...
... Then I dealt with Fizeau's experiment and tried to approach it with the hypothesis that the equations for electrons given by Lorentz held just as well for the system of coordinates fixed in the moving body as for that fixed in the vacuum...
... Why are these two things [constancy velocity of light and classical velocity addition] inconsistent with each other? I felt that I was facing an extremely difficult problem. I suspected that Lorentz's ideas had to be modified somehow, but spent almost a year on fruitless thoughts. And I felt that was puzzle not to be easily solved."
From a lecture given in Kyoto, Dec. 14, 1922. Notes by Jun Ishiwara in Japanese; translation assembled from various published translations.
Lorentz and Einstein both considered the same two cases in their reflections on aberration:
 |
 |
||
| Star at rest. Earth moves | Star moves. Earth at rest. |
For Lorentz, these were two very different cases. "At rest" meant "at rest in the ether." So the two cases differ in the fundamental fact of what is absolutely at rest and absolutely in motion.
For Einstein, convinced of the correctness of the principle of relativity well before 1905, the two cases must be read rather differently. He did not believe there was such a thing as the absolute motion that Lorentz believed separated the two cases. The designation "at rest" was merely a statement of the frame of reference in which we choose to describe the process. For him the two cases were merely the same physical system, but now viewed in two different frames of reference.
So Einstein would read changes in the transition between the two cases as merely the outcome of a change of frame of reference. We move from a frame of reference in which the star is at rest to one in which the star moves. One outcome of the change is that the earth that was in motion is now brought to rest.
There is another change associated with the transition between the two frames: the wavefronts of the propagating plane waves are rotated. That is simply an artifact of the change of frame of reference. But how could a change of frame of reference bring about this sort of rotation? We have seen above in Section 4 through the example of the moving rod that this effect arises directly as an expression of the relativity of simultaneity. Lorentz's analysis has given a mathematical description of the effect. We assemble the way the system appears in the new frame of reference by sampling from the way it appears in the old. But we sample at different times from different places according to Lorentz's rule t' = t - (v/c2) x, for the case of v very much smaller than c.
This was not the way Lorentz saw it. But it is the way Einstein must see it if he adheres to the principle of relativity. For there can be no factual difference between the two cases. Any difference must be an artifact of the description in the frame of reference chosen. So the two cases simply display a new fact about time: judgments of simultaneity differ according to the frame of reference used for description. And Lorentz's rule simply is the rule for transforming time between two frames of reference in relative motion.
This is the fascinating question, for this discovery marks the end of Einstein's journey of seven and more years through puzzles in electrodynamics and perplexities over light to a new theory of space and time. We have long held the default supposition that the discovery was made along the same lines as it was presented in the 1905 special relativity paper: that Einstein found it by mulling over clocks and how they might be synchronized by light signals.
Yet we have no direct evidence for this default supposition. Einstein certainly never says it was how he discovered the relativity of simultaneity. Unfortunately none of his recollections of the background to the discovery of special relativity give enough detail to enable us to know assuredly he did it. However what is striking about those few recollections we do have is that they do not pertain to light signals--short pulses of light used to set clocks or other devices. Rather they pertain to problems in electromagnetic theory. And if light does enter into them, it enters as it is treated in electromagnetic theory, that is, as a propagating waveform.
So we must entertain the possibility that Einstein found the relativity of simultaneity by another pathway and that the formulation and presentation of the 1905 special relativity paper was found later. My conjecture is that the discovery actually happened through Einstein's examination of Fizeau's experiment and stellar aberration in the context of Lorentz's Versuch. I cannot assure you that it is what happened. But I can assure you that everything fits pretty much as well as we could expect given the fragmentary nature of our evidence.
We know Einstein treated light as a propagating waveform prior to the discovery. Light enters the proposed analysis in both cases as a propagating waveform. We know that Einstein read Lorentz's work of 1895 and that he reflected upon these two experiments. And the proposal is that Einstein, convinced of the principle of relativity, would have to reinterpret Lorentz's work in a quite specific way: the relativity of simultaneity is expressed quite directly in the rotation of the propagating wavefronts of stellar aberration. Although I have not reviewed the details here, a short algebraic analysis shows that the relativity of simultaneity is expressed equally clearly in the result of Fizeau's experiment on the speed of light in moving water. What I propose is that, after much travail, Einstein finally saw that expression and thereby discovered the relativity of simultaneity.
All this fits well with Einstein's remark quoted above in the Kyoto lecture: "I suspected that Lorentz's ideas had to be modified somehow..." and also with the terse but familiar characterization Einstein gave of special relativity in 1907: "One needed only to realize that an auxiliary quantity that was introduced by H. A. Lorentz and that he called 'local time' can simply be defined as 'time'."
There is one final consideration that makes the above proposal appealing. For Lorentz, the introduction of local time was justified ultimately by Maxwell's electrodynamics. Its use was dependent upon his theorem of corresponding states, whose proof required the full content of Maxwell's theory. So Lorentz's inferences proceed according to:
| Maxwell's electrodynamics. |
TO | Theorem of corresponding states. Local time. |
TO | The observable deflection of stellar aberration conforms to the principle of relativity. |
Einstein's analysis, however, proceeds in the reverse direction, starting with experimental results:
| Stellar aberration conforms to the principle of relativity. |
TO | Local time simply is time. |
That is, Lorentz's analysis was dependent upon the presumption of Maxwell's electrodynamical theory. Einstein's reanalysis, however, was freed from this dependence. He needed only to presume that the principle of relativity was upheld and to combine it with known experimental results--stellar aberration and Fizeau's experiment--to arrive at the relativity of simultaneity. This decisive result is read directly from experimental or observational results. That surely would make the result compelling, since it was freed from any encumbrance with the complications of Maxwell's electrodynamics. Perhaps it would even be compelling enough to embolden Einstein to discard the most successful theory of space and time so far seen in the history of science and which had reigned for nearly a quarter of a millennium.
Copyright John D. Norton, April 9, 2005. Rev. April 10, 14, 2005. Minor revisions April 21, Nov. 6 2005.