John D. Norton
Department of History and Philosophy of Science
Center for Philosophy of Science
University of Pittsburgh
This page at at www.pitt.edu/~jdnorton/Goodies.
The text here is an expanded and edited version of Section 4. "A New Phase-Volume Based Exorcism of Maxwell's Demon" in John D. Norton, "All Shook Up: Fluctuations, Maxwell's Demon and the Thermodynamics of Computation," Entropy, 15 (2013), pp. 4432-4483.
This exorcism is set within classical physics. It is easy to generate a quantum version by some simple substitions of quantum analogs for classical parts of the analysis. See "The Simplest Exorcism of Maxwell's Demon: The Quantum Version."

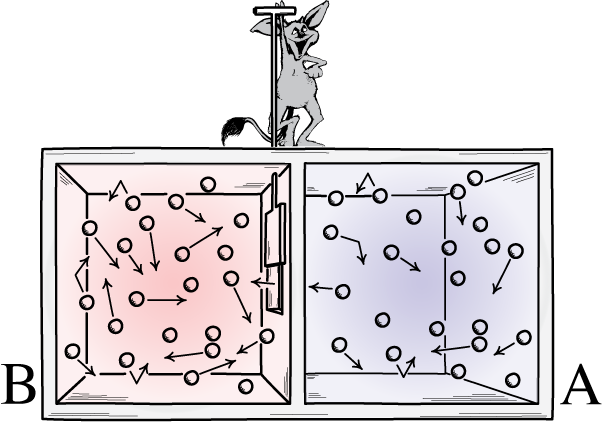
In letters from 1867 and 1871 and then in his 1871 Theory of Heat, James Clerk Maxwell described a tiny demon who could reverse the second law of thermodynamics. The demon simply opened and closed an opening between two portions of a vessel filled with air so that the faster molecules collected one on side "B" and the slower ones on the other side "A". The slide operated by the demon is assumed to be very light, so that negligible work is done during the operation.
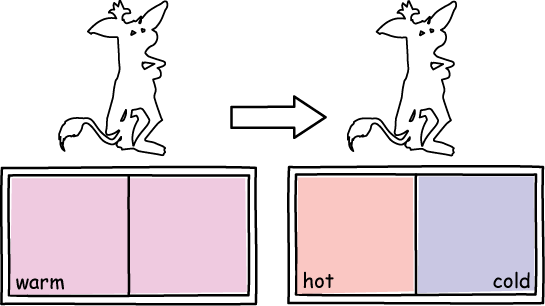
The net effect is that we start with a vessel filled uniformly with warm air.
B 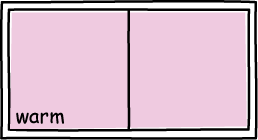 A
A
When the process is finished, side B is hotter and side A colder while no work has been done.
B  A
A
This violates the second law of thermodynamics.
Maxwell himself maintained that this thought experiment presented no special challenge to our science. It merely reveals that the second law fails if it is possible to manipulate molecules individually. For Maxwell's text from the 1972 edition of Theory of Heat, click here.
Later thinkers felt differently. Maxwell's demon must fail to reverse the second law, they felt. The problem became how best to argue for its failure; that is, how best to exorcise the demon. As far as I know, everyone now agrees on the first step: the demon is naturalized. That means that it must be just another, ordinary physical system, even if it is a miracle of micro-engineering. Now we must seek something in its constitution that would ensure its failure.
Marian Smoluchowski gave the best completion of the analysis in 1912. He argued through many examples that thermal fluctuations within the demonic machinery would so disrupt it that it must fail in its intended operation.
A later tradition ignored Smoluchowski's recognition of the importance of fluctuations. Starting with Leo Szilard's work of 1929, that tradition sought to base the exorcism on an entropy cost associated with the processing of information. That cost would be enough to undo the reduction in entropy brought about by the demon and thus to save the second law.
Szilard attributed the cost to processes that ascertain the state of a system of interest. Landauer and Bennett attributed the costs to dissipation that they believe is associated with erasing a computer memory.
This information based tradition is initially intriguing and appealing, until one asks after the details of the analysis. Elsewhere I have argued that these essential details have never been provided adequately. Rather the information-based analysis is an enduring collection of mistakes and confusions. For more see my papers.
For over eighty years, we have focused on the information-based approach to exorcism. Enthusiasts for it have sought to make the analysis work. Critics--myself included--have sought to show that the information-based approach fails. As a result, we have overlooked a much simpler exorcism that makes no use of the notion of information. It is described here.
The exorcism characterizes the demon as a little machine that obeys ordinary physical laws. Specifically it is governed by Hamiltonian mechanics, which is about as general and generic as a physical system can be. Associated with Hamiltonian mechanics is the idea of phase space. It is a huge space of very many dimenions each of whose points represents one state the of the thermal system and demon together.
A simple but quite powerful exorcism derives from an apparently innocuous part of a straightforward description of what a Maxwell’s demon must do. It is the assumption that the demon, when placed in a generic thermal environment, will always, or even just very likely, succeed in moving the thermal system far from its equilibrium state.
We shall see that when this condition is translated into the language of Hamiltonian mechanics, it tells us that the time evolution induced by the demon is one that compresses the set of states in the phase space.
That requirement conflicts with Liouville’s theorem in Hamiltonian mechanics. The theorem says that volumes of phase space cannot be compressed or expanded by the evolution of the systems under Hamiltonian mechanics.
To begin, we need a description of what the demon does:
(a) A Maxwell’s demon is a device that, when coupled with a thermal system in its final equilibrium state, will, over time, assuredly or very likely lead the system to evolve to one of the intermediate states defined below; and, when its operation is complete, the thermal system remains in the intermediate state;
This description is reasonable since a device is not a properly functioning Maxwell’s demon if it only succeeds occasionally when coupled to some larger thermal system, but mostly fails. A device that sometimes “gets lucky” in reversing the second law of thermodynamics is a lesser demon and one to which this exorcism does not apply. Similarly, the reduction must persist. A momentary reduction is compatible with a very unlikely and fleeting fluctuation to an intermediate state.
(b) The device returns to its initial state at the completion of the process; and it operates successfully for every microstate in that initial state;
As a result, there is no degradation of the state of the device that might comprise an unaccounted source of dissipation that could protect the second law of thermodynamics. (note 1)
It is also assumed that:
(c) The device and thermal system do not interact with any other systems;
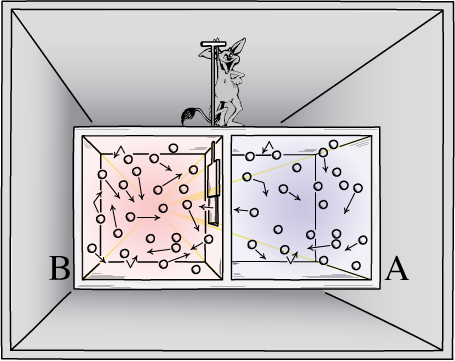
A device that can perform as in (a), (b) and (c) is violating the second law of thermodynamics. It is undoing a spontaneous change in a thermal system without compensating dissipation elsewhere, for the device returns to its original state and does not interact with any other systems.
For example, the device might lead a gas of uniform temperature and pressure to separate out into parts of different temperature or pressure. Either of these disequilibria could then be exploited to generate work whose energy would be derived completely from the thermal energy of the final equilibrium state. The net effect is a conversion of heat into work without discharge of heat to a cooler place, in violation of the second law of thermodynamics.
We now need some assumptions about how the demon is constituted:
(d) The time evolution of the total system is Hamiltonian with a time-reversible, time-independent Hamiltonian;
This assumption is near universal in the literature on statistical physics and is normally regarded as benign. (note 2) Breaches of (d) are conceivable, although not normally arising in systems commonly investigated in physics. They may enable Maxwell’s demons and violations of the second law of thermodynamics. The Zhang and Zhang “pressure demon” described in Appendix 2 of Earman and Norton appears to be such a case. (note 3)
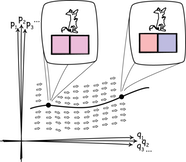
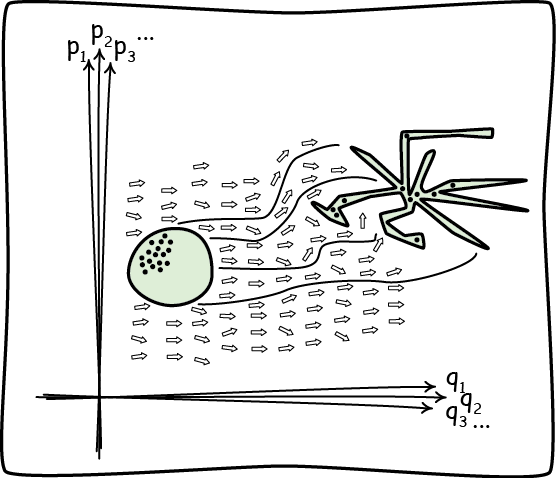
Each system in Hamiltonian mechanics can be characterized by a large number of variables: the positions and orientations of each its components (q1, q2, q3, ...) and the all momenta associated with them (p1, p2, p3, ...). These variables taken together form a phase space. Each point in the phase space corresponds to a complete system.
These systems evolve over time. A system that starts at one point in the phase space will move to another and then another as time passes. The trajectory it traces in phase space is its complete history.
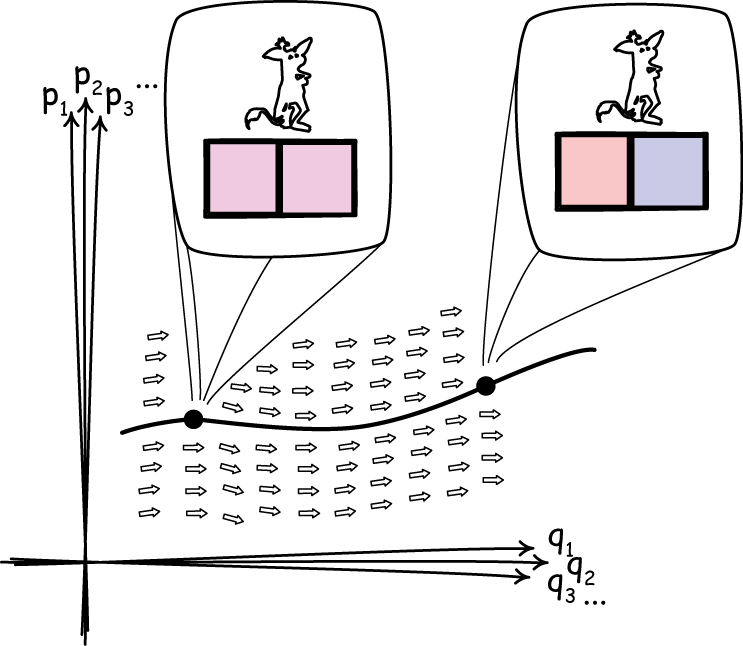
Hamilton's equations tell us how each system will evolve. The import of the equations is to fill the phase space with the little arrows shown in figure. A system evolves merely by following the direction indicated by the arrows. What results is a "Hamiltonian flow" over the phase space.
The demon moves a thermal system away from its equilibrium state. Hence we need to introduce some assumptions about the nature of equilibrium states.
If it is not coupled to a demonic device, we will assume that a thermal system will revert spontaneously to some final, equilibrium macroscopic state. A common example is that a gas will spontaneously equilibrate to uniform temperature and pressure, while expanding to fill the space available.
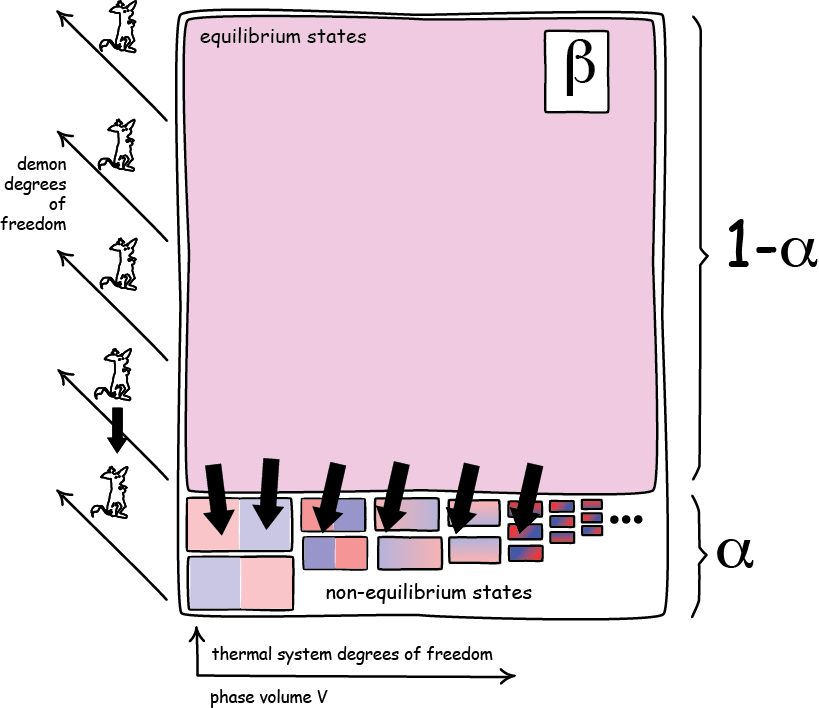
One of the most important facts in thermal physics is that an equilibrium state comprises very many microstates. There are so many that they all but completely fill the thermal system’s phase space. Non-equilibrium states, such as a gas that is momentarily hotter on one side and colder on another, all reside in a tiny portion of the phase space.

To get a sense of just how completely the microstates of an equilibrium state will fill the phase space, consider how a mole of a dilute gas at thermal equilibrium is distributed over the configuration space portion of the phase space. It has N = 6.02 × 1023 molecules. The fraction of its molecules at any moment in the left half of the chamber holding the gas is roughly 0.5. More precisely, the fraction is binomially distributed over the two halves. Using the central limit theorem, the fraction of molecules in the left half is distributed normally with a mean of 0.5 and a standard deviation of 1/2 N1/2 = 6.444 × 10-13. We know that virtually all gas samples, that is a fraction 0.999999998027 of them, will be within six standard deviations of this mean of 0.5. That is, all but a fraction α = 0.000000001973 will lie in the interval:
0.5 ± 6 × 6.444 × 10-13 = 0.49999999999613 to 0.50000000000386
In short, the equilibrium states virtually fills the phase space completely. Other macroscopic states—here called “intermediate states”—are ones that will spontaneously move to the final, equilibrium state if an accessible pathway is available.
A common example is a body with an uneven temperature distribution: the temperatures will equilibrate if a thermally conducting channel connects the parts. Another is a gas with uneven pressure: the pressures will equilibrate if the partition separating the parts of unequal pressure has a hole in it.
These states are macroscopically distinct from the final equilibrium state and must all be found in the very small part of the system’s remaining phase space. It is assumed here that the demonic device acts on a thermal system of this type; that is, with an equilibrium state that occupies virtually all its phase space.
The following summarizes the discussion above:
(e) The final equilibrium state occupies all but a tiny portion α of the thermal system's phase space, V, where α is very close to zero;
(f) The intermediate states are all within the small remaining volume of phase space, αV.
V 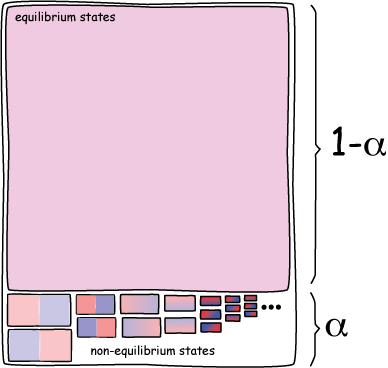
In operation, the device is coupled to the thermal system in its final, equilibrium state. The thermal system evolves to an intermediate state, while the device returns to its initial state, which occupies a volume v of the device phase space. We assume in (a) that the device will operate as intended for virtually all of the microstates comprising the final equilibrium state. Let us say that it succeeds for all but a small fraction β of these microstates. That means that demon is successful for states occupying a volume
(1-α)(1-β)V
of the thermal system phase space.
The demon will move the system away from the equilibrium state. Hence the resulting system must be found somewhere in the small remaining portion of the thermal system's phase space,
αV.
Finally, we must consider the volumes of phase space associated with the thermal system and demon together. So we must multiply both of these volumes by the initial and final phase volume of the demon, that is, by v.
The overall effect of the operation of the demon is to take all the microstates in some large volume of the combined phase space,
v(1-α)(1-β)V,
and compress it to one that is much smaller, that is, less than
vαV;
and for it to remain there. Since α is very close to zero and β quite small. It follows that
vαV < v(1-α)(1-β)V.)
Now comes the problem: the time evolution of the total system is a Hamiltonian flow. As a result Liouville's theorem obtains. It requires that the combined phase volume is conserved under time evolution. It cannot contract under Hamiltonian time evolution.
That is, consider the set of states in the green volume at left. Under the Hamiltonian flow, the volume will migrate through the space. Generically, the volume will rapidly form an extremely convoluted structure will fine tendrils thrown off in all directions. However, no matter how complicated the tendrils, the total volume of the evolved structure will remain the same.
The specification of the operation of a Maxwell's demon requires that it compresses the phase space. Liouville's theorem says that this compression is impossible. Therefore the operation of the demonic device is impossible.
This conclusion completes the exorcism. (note 4) (note 5)
What makes this exorcism quite robust is that it avoids more tendentious assumptions:
(i) The second law of thermodynamics is not assumed to hold, so that the circularity troubling the information-theoretic exorcisms does not arise;
(ii) The volumes of phase space representing states are not coarse grained; they consist simply of all those microstates upon which the demon can successfully act and the states that result;
(iii) Thermodynamic entropy is not included in the argumentation.
Condition (ii) avoids the complication that coarse-grained volumes can expand and compress under Hamiltonian time evolution, according to how we include or exclude the microstates in the volume through the coarse graining procedure. The description of the demon requires that we cannot neglect microstates associated with the macroscopic equilibrium state, for the demon must succeed with all or virtually all of them. (note 6)
Condition (iii) reflects a caution not normally observed. If we leave open the possibility that the second law of thermodynamics fails, then the normal definitions of thermodynamic entropy either lose the factual grounding needed for their statement or lose familiar consequences.
Take the “Clausius” definition that relates thermodynamic entropy to heat. If the second law fails, we cannot be assured of the fact of path independence of its central quantity
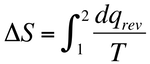 ,
,
computed for some thermodynamically reversible process connecting two states 1 and 2. So we cannot be assured that the entropy it defines is a state function.
We might replace it with a Boltzmannian
“S = k log (phase volume)”
as the new definition. However we would no longer be assured that entropy defined this way relates to heat according to the Clausius formula. Since thermal systems need no longer evolve to states of maximum phase volume, “S = k ln (phase volume)” would no longer coincide with “S = k log (probability).”
If we are cautious, the exorcism can be redescribed in terms of entropy. The final and intermediate states would be redescribed as higher and lower entropy states. To avoid problems, we would need to assume that all ascriptions of thermodynamic entropy are made in contexts in which the second law of thermodynamics holds. That is, the ascriptions would all carry a tacit rider that says “in so far as we deal with states and processes not coupled to demonic devices.”
How does this exorcism look when applied to an example? How does it compare with an information-theoetic exorcism?
The Smoluchowski trapdoor is one of the simplest mechanical demons. Instead of an intelligent being operating the door in the vessel Maxwell described, we simply have a lightly spring-loaded door. The door can only open one way. The intent is that air molecules hitting the door from one side open it and allow the molecules to pass. However the door cannot swing the other way, so return passage is possible. The net effect, it is supposed, is the the air in the vessel accumulates on one side, in violation of the second law.
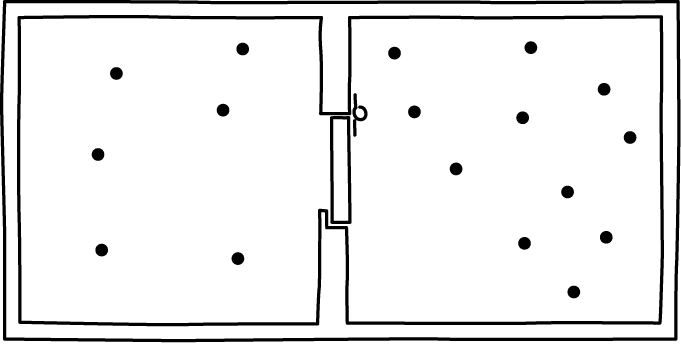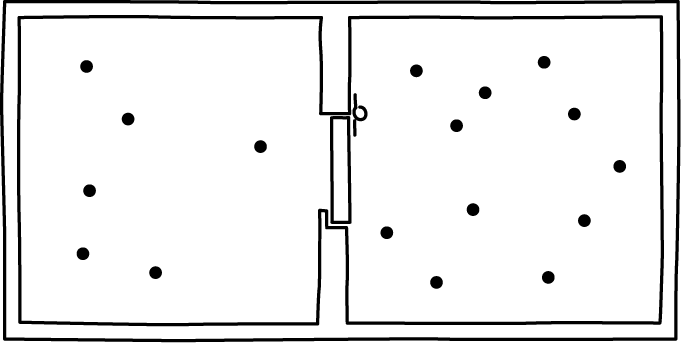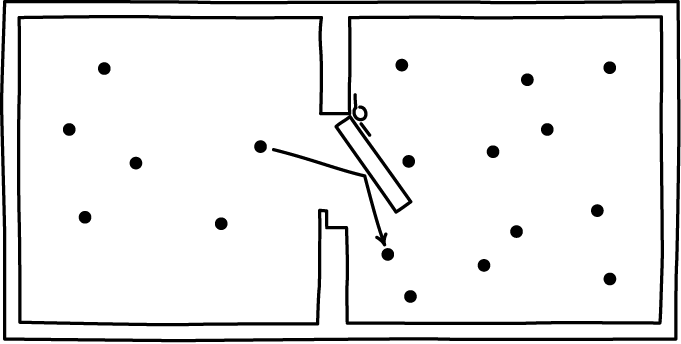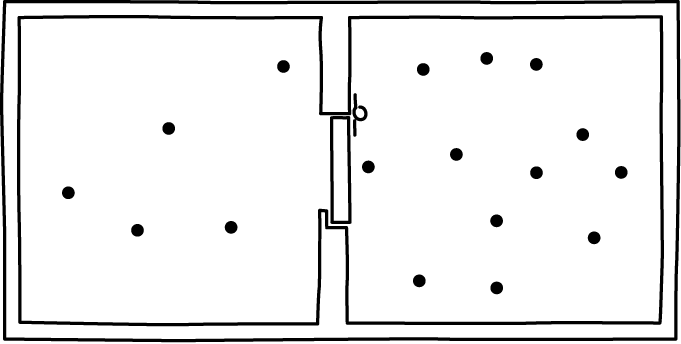
If the device operated as described here, this is what would happen. It would start with air uniformly distributed over both sides of the vessel. That uniform distribution corresponds to virtually all of the volume of the air's phase space. The end state would be the air compressed to one side. That state corresponds to a minute fraction of the air's phase space.
The demon--that is, the spring loaded door--would routinely return to its closed state. So, we can choose that as its start and end state. The two states have the same phase volume in the trapdoor-spring phase space.
Thus the net effect of the intended operation would be an enormous compression of the combined air-demon phase space.
Since the gas and spring-loaded door are a Hamiltonian system, Liouville's theorem prohibits this compression. The trapdoor demon cannot function as intended.
What happens? Smoluchowski pointed out that the trapdoor must itself be very light and very lightly spring loaded if a collision with one air molecule is to open it. As a result it has its own random motion due to thermal fluctuations and is, of its own accord, flapping about in a way that is uncoordinated with the motion of the molecules in the air. Thus, it lets air molecules pass freely in both directions and no accumulation of air on one side can happen.
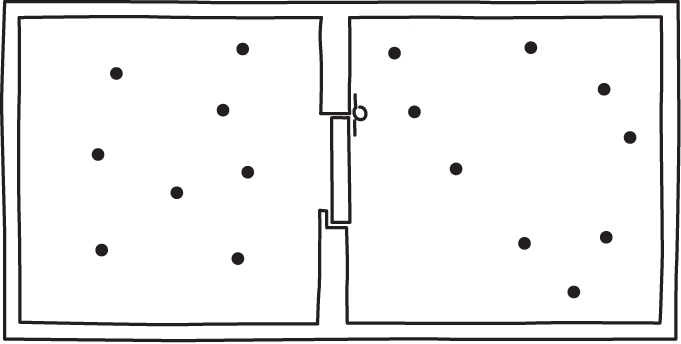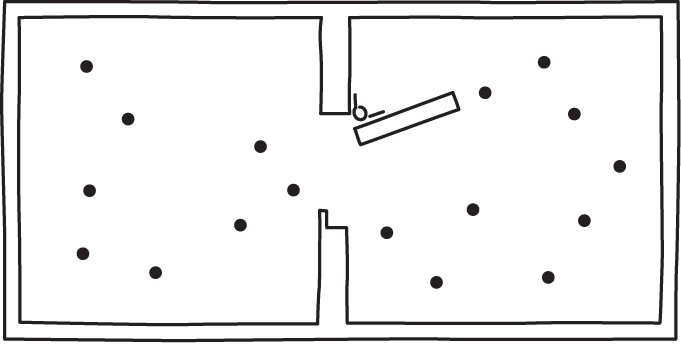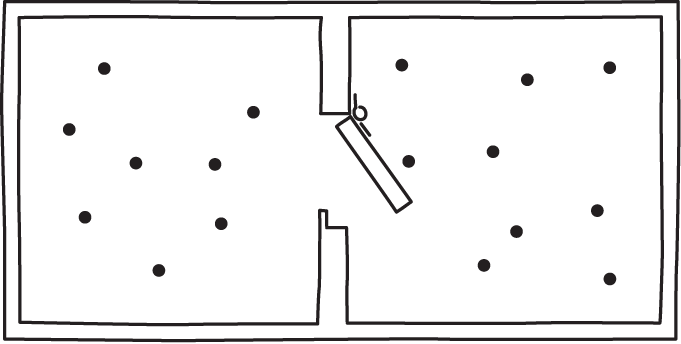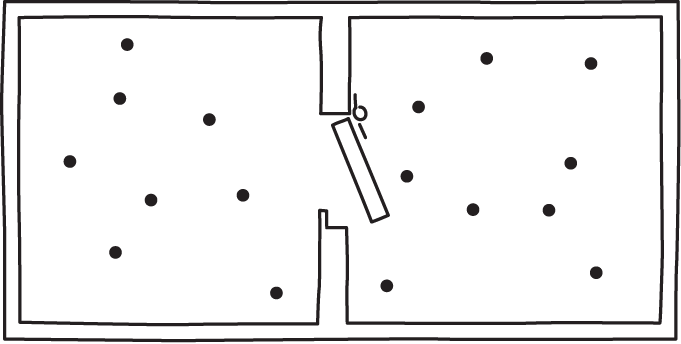
The Smoluchowsi trapdoor is a simple test for any proposed exorcism of Maxwell's demon. It is immediately obvious that an information based exorcism is of no use. The are no sensors in this simple device that collect information; and there are memory devices that would need erasure if the demon is to return to its original state.
1. In his Chapter 5, Albert drops this condition (b). He concludes that a Maxwell’s demon can reduce a target system’s thermodynamic entropy without violating Liouville’s theorem if the demon ends in different macrostates. A difficulty with the proposal is that it requires a physical process that can reliably amplify the demon’s microstate to a macrostate. The no-go result of "All Shoook Up..." suggests that fluctuations will interfere and that the amplification will require creation of thermodynamic entropy. Without further details, we cannot preclude the possibility that this created entropy is greater than the entropy reduction in the target system.
2. Neither time-reversibility nor time-independence of the Hamiltonian is needed for the Liouville theorem. However it is needed to preclude systems that do not exhibit ordinary thermodynamic behavior. For example, replace the standard one-dimensional, free particle Hamiltonian H = p2/2 by a time-irreversible H = p3/3. If p and q are the usual canonical coordinates, Hamilton’s equations now yield p = constant and dq/dt = p2 = constant ≥ 0. The free particle is no longer indifferent to direction in space but must move uniformly in the +q direction if it moves at all. Presumably a confined gas of these particles would accumulate at one confining wall.
3. We tried to demonstrate in Earman and Norton that the equations governing the pressure demon cannot be written in Hamiltonian form. An unfortunate lacuna was our unproven assumption that ordinary particle velocity would have to be the canonical momentum appearing in the applicable Hamiltonian equations.
4. A small technical point: I have assumed that the phase volume of the demon state remains the same volume v upon completion. It cannot increase, for then condition (b) would be violated. If it were to decrease to some subvolume v’<v of the initial volume, then Liouville’s theorem requires a corresponding increase in the ratio v/v’ of the thermal system phase space. That increase is ruled out since the ending phase volume of the thermal system is already too large to expand appreciably.
5. Does this exorcism contradict Poincaré recurrence? According to the recurrence, a closed system with finite phase volume returns arbitrarily closely to its initial state, typically after eons of time, under Hamiltonian time evolution. There is no contradiction, for Poincaré recurrence does not require that all microstates in the final equilibrium state revert to an intermediate state at the same time and then remain there. Rather they will each do it at different times and then immediately revert to the final equilibrium state. That behavior is not proscribed by Liouville’s theorem since different subvolumes of the final equilibrium state will revert at different times to produce an intermediate state momentarily.
6. In their Chapter 13, Hemmo and Shenker also investigate the prospects of Maxwell’s demon through phase volume dynamics. They infer the possibility of the demon since, in part, their analysis employs coarse-grained volumes of phase space.
Albert, D. Time and Chance; Harvard University Press: Cambridge, MA, USA, 2000.
Earman, J.; Norton, J.D. Exorcist XIV: The wrath of Maxwell’s demon. Part II: From Szilard to Landauer and beyond. Stud. Hist. Philos. M. P. 1999, 30, 1–40.
Hemmo, M.; Shenker, O.R. The Road to Maxwell’s Demon: Conceptual Foundations of Statistical Mechanics; Cambridge University Press: Cambridge, UK, 2012.
December 31, 2013. Copyright John D. Norton.