John D. Norton
Department of History and Philosophy of Science
University of Pittsburgh, Pittsburgh PA 15260
Homepage: www.pitt.edu/~jdnorton
This page (with animated figures) is available at www.pitt.edu/~jdnorton/goodies
Thought experiments can sometimes appear magical in their ability to produce interesting results with astonishingly little effort. But sometimes the magic can get out of hand. That happens when we have two apparently equally good thought experiments that yield contradictory results. Here are two examples:
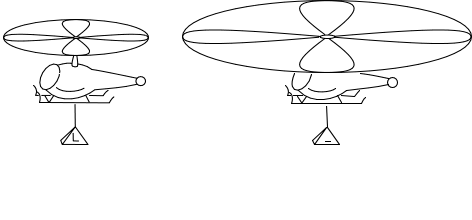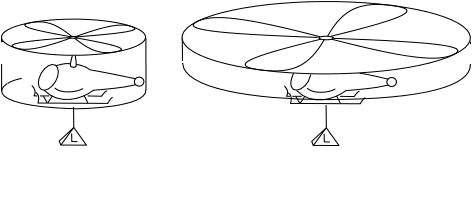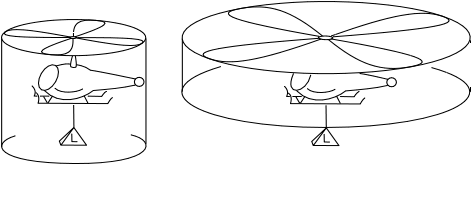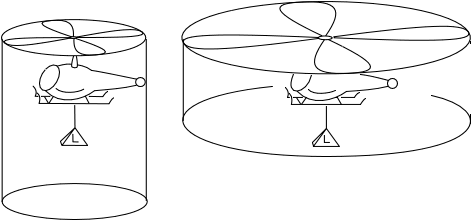
Imagine a helicopter rotor. When it rotates, it generates lift as a reaction force resulting from the momentum imparted to the current of air it directs downward. If the rotor moves a mass m of air in one second at speed v, then the lift L generated is just mv.
What would happen if we double the radius of the rotor?
To answer, let us assume that it is part of the design of rotors of varying size that the speed of the air currents they generate is proportional to the rotational speed of the rotor. (This can be achieved by flattening the rotor blades more, further from the center.) Since the area swept by the rotor has increased by a factor of 2x2 = 4, if we leave the rotational speed of the rotor fixed, in one second the rotor will move a mass 4m of air at speed v. So the lift will have increased by a factor of 4 to 4mv. To keep the lift constant at L = mv we should now also reduce the rotational speed of the rotor by a factor of 2. That halves the speed of the air to v/2 and also halves the mass moved from 4m to 2m. The lift is now (2m).(v/2) = mv = L, which is the original lift.
In short, the lift stays constant at L as we double the rotor size and halve its speed.

Repeat this process endlessly in thought, indefinitely doubling the rotor size and halving the rotational speed. In the limit of infinitely many doublings, we have a rotor of infinite size that is not rotating but still generates the original lift L.
So we conclude:An infinite helicopter rotor at rest generates lift L.
Incidently: The (minimum) power required to sustain the lift is just the kinetic energy of the air moved per unit time, that is P = mv2/2. So in this process the power is halved to (2m)(v/2)2/2 = mv2/(2x2) = P/2. Thus in the limit of the infinite rotor, no power is needed to sustain the lift L. "That must be how angels work. Wide wing spans." -- Jeremy Butterfield.
The obvious anti-thought experiment yields no lift for an infinitely large rotor at rest.
A finitely sized rotor that does not turn generates no lift. This is true if we double its size. In the limit of infinitely many doublings we have an infinitely large rotor that does not rotate and generates no lift.

So we conclude: An infinite helicopter rotor at rest generates no lift.
At a decisive moment in the course of his discovery of the general theory of relativity, sometime in 1912, Einstein realized that the geometry of space for an accelerated observer may be non-Euclidean. He showed this for the case of a uniformly rotating observer in special relativity by means of a thought experiment concerning a rigidly rotating disk.
| Einstein imagined that the geometry of the surface of the disk is investigated by the usual method of laying down measuring rods. If the disk's diameter is D, then we will find the circumference C to be given by C = pi x D, the familiar Euclidean formula. |
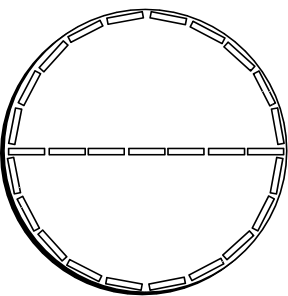
|
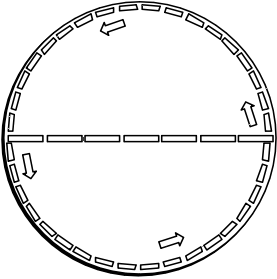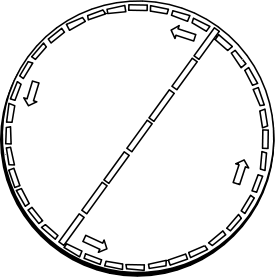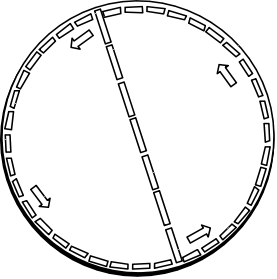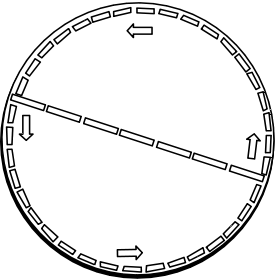
|
Now imagine that the disk is rotating uniformly.
What will we measure for its circumference C? Will it be the Euclidean C = pi x D? The lengths of measuring rods laid radially are not affected by the Lorentz contraction of special relativity since their motion is perpendicular to their length. But rods laid tangentially along the circumference move in the direction of their length and will be contracted. So more rods will be needed to cover the circumference than according to Euclidean expectations. That is, we will measure a non-Euclidean C > pi x D. |
|
Einstein's thought experiment gives a non-Euclidean geometry with C > pi x D, an anti-thought experiment gives the opposite result of a geometry with C < pi x D. The alternative was proposed, for example, by Joseph Petzold in a letter to Einstein of July 26, 1919. It is, in effect, that the rotating disk be conceived as concentric, nestled, rotating rings. As before the rings are uncontracted in the radial direction by the Lorentz contraction of special relativity, since the rings do not move in that direction. So the diameter of the disk is unaffected. But the rings are contracted in the circumferential direction, the direction of their motion due to the rotation. So their circumference is less that the corresponding Euclidean length. That is, the lengths on the disk conform to C < pi x D. |
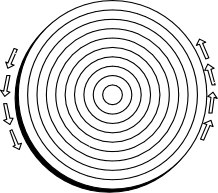
|
|
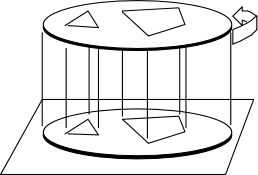
Another anti - thought experiment, investigated by Ehrenfest in 1910 and Varicak in 1911, gives the Euclidean result. The positions of distance markers on the rotating disk are transferred at some instant to superimposed but non-rotating tracing paper and the geometric figures on the disk reconstructed. The result, Varicak urged, would be recovery of Euclidean figures because the surface of non-rotating tracing paper conforms to Euclidean geometry. So C = pi x D |
We learn something important about thought experiments from this little game. Thought experiments are supposed to teach us things about the world. Einstein certainly used them in an important way in many of his discoveries. The philosophical challenge is to figure out how they can do this. Are they, as their name suggests, able to do what real experiments do, but without the costly inconvenience of execution? Some say that they can. I just don't believe it. To them I say this.
Thought experiments can err. These thought experiment/anti-thought experiment pairs show that quite clearly. At most one in a pair will be delivering the right result. If thought experiments are to be reliable instruments of inquiry, then we must have some way of adjudicating between competing thought experiments. I urge that if we pursue this demand we end up with the conclusion that thought experiments are merely picturesque arguments, in highly disguised form. If they are anything else, I urge, they would become useless as instruments of inquiry, since we would have no way to adjudicate between good and bad thought experiments.
Thought experiments, in the end, have no more magical powers epistemically than ordinary argumentation. Real-life experimenters need not fear for their livelihoods!
For the details (and for references to the literature on the rotating disk thought experiments), see John D. Norton, "Why Thought Experiments Do Not Transcend Empiricism" pp. 44-66 in Christopher Hitchcock (ed.) Contemporary Debates in the Philosophy of Science. Blackwell, 2004.
John D. Norton, January 2005. Reformatted April 14, 2005 on a transatlantic flight returning to Pittsburgh from the Israel Academy of Science and Humanities conference on Einstein.