





John D. Norton
Center for Philosophy of Science
Department of History and Philosophy of Science
University of Pittsburgh
This page at www.pitt.edu/~jdnorton/Goodies
| Elsewhere, I have urged that there is no universal logic of inductive inference. Rather the inductive logic appropriate to a given domain is fixed by the particular facts that that prevail there. It is easy to give quick and simple examples of this sort of thinking. The trouble is that these examples are just that: they are quick and simple, so the whole thing looks frivolous. What's needed is a weightier example that shows more clearly what I have in mind. That is what I'm going to lay out here. | Elsewhere? Where!? See "A Material Theory of Induction." "A Little Survey of Induction." |
It is possible to have non-probabilistic, indeterministic systems in physics. These are systems whose past state fails to fix their future states and does not even give probabilities for the different possible futures. I don't assume that there really are such systems. All I assume is that they are a perfectly respectable possibility and that, if we lived in a world with them, we would expect to be able to infer inductively about them. The principal claim is that their odd physics determines a correspondingly odd, non-probabilistic logic of induction.
| This example is developed in Section 8.3 of "Probability Disassembled" and in "Induction without Probabilities." | The story will unfold using a particular example of an indeterministic system, "the dome." That example is used solely for concreteness and expository convenience. Nothing in the general argument depends on the details of the dome example. |
If one idea about inductive inference has taken root in recent philosophy of science, it is that inductive inference and probability theory are intimately connected. Indeed many people seem to believe that probability theory provides the One True Logic of induction. Probability theory didn't start out that way. It was originally developed as a physical theory, the theory of chances associated with gambling. Very soon, it was noticed that probabilities behaved just like we'd want degrees of belief to behave. The connection to inductive inference was made.
We now tend to use the word "probability" in two senses reflecting these two uses. Sometimes it refers to a physical property of a system. There is probability of a half that a coin tossed fairly will come up heads. Sometimes it refers to our degree of belief. I may entertain a probability of half that it will rain today, so I take an umbrella.
There are occasions in which we will want to combine the uses. What should my degree of belief be that a coin tossed fairly comes up heads? The objective probability--the chances--are a half. So it seems inescapable that I should set my subjective, probabilistic degree of belief equal to that same half. In his celebrated "A Subjectivist's Guide to Objective Chance," David Lews laid out his "PrincipalPrinciple." In effect it says just that. If there are objective chances to be had, your subjective probabilities should match them.
 |
 |
 |
 |
 |
 |
Look at what just happened. We want to know what our degrees of belief about a coin toss should be. We notice which physical facts goven the coin toss. Those physical facts then determine what our degrees of belief should be. Indeed the notion is strong enough to determine not just what the degrees of belief should be, but what rules govern them. The objective chance of getting a head or a tail is just the sum of the objective chances of each outcome individually. So our subjective degree of belief of getting a head or a tail must be the sum of our subjective belief in each individually.
That seems to me to be just one illustration of a broader idea. The physical facts that prevail in some domain fix the inductive logic appropriate to that domain. That this circumstance is universally so is the central idea of the "material theory of induction." It says that inductive inferences are not ultimately licensed by universally applicable logical schemas, as is the case in deductive inference. Rather, when we seek the grounding of an inductive inference, our search ends in material facts that hold only locally. In the case of the coin toss, it ends in the stochastic properties of tossed coins. Our degrees of belief ought to conform to the probability calculus just because the physical chances of the coin tosses conform to that same calculus.
| Or another example: once we know the mass of one (or a few) electrons, we know the mass of them all. But once we know the mass of the star that is our sun, we certainly don't know the mass of all stars. Why does the inference from "one..." to "all..." work in one case but not the other? It is the same inference form. Both infer from "one..." to "all..." It works where it does because of the prevailing facts. Electrons are factually like that. They are fundamental particles and fundamental particles of one type generally all have the same mass. Know the mass of one and, generally, you know the mass of them all. That fact licenses the inference. Stars are not governed by the same facts, so the same inference form cannot be used for their masses. | The "generally" has to be added. Another type of fundamental particle, the neutrino, comes in varieties that turn out, on recent research, to have different masses. The "generally" is important. It makes the inference inductive. Otherwise we'd just deduce the mass of all electrons from one. |
Let's try for a more interesting example. The dome--as described elsewhere in these pages--is an indeterministic, Newtonian system. A mass sits at the apex of a dome. In full conformity with Newtonian theory, it may remain there for ever; or it may spontaneously move away from the apex in any direction at any time T. It is a true case of indeterminism. There are no hidden processes that I'm ignoring that might fix the time T of spontaneous motion. The mass is not bumped off the dome apex by unnotice vibrations in the dome; or by enough random collisions with air molecules to dislodge it. The example is sufficiently idealized so that no such processes are at work. It is manifestation of a less recognized fact about Newtonian physics. Some of its systems are just indeterministic.
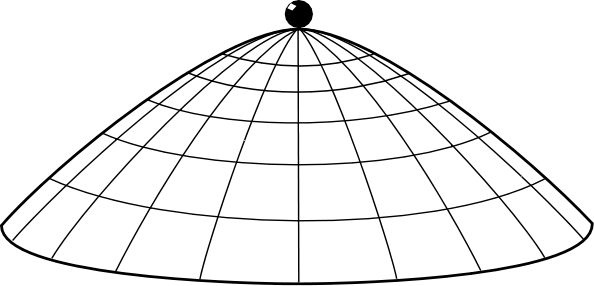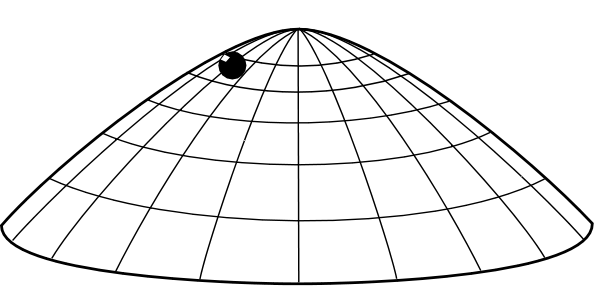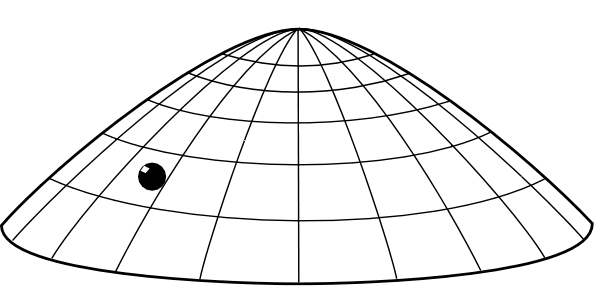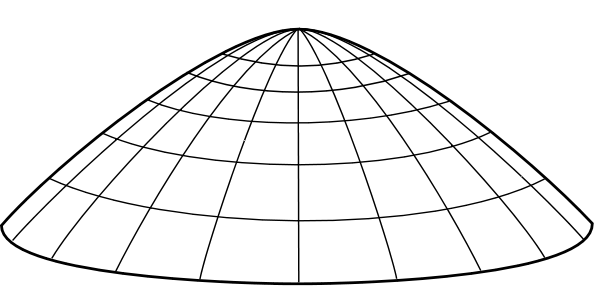
For present purposes, however, the important fact is this: Newtonian theory provides no probabilities for the time of spontaneous motion T or the direction of the motion. It merely says spontaneous motion at this or that time T is possible. This is such an essential point that it is worth repeating. Newtonian theory provides no probabilities for the time of spontaneous motion T or the direction of the motion.
So the question is: given that we know the mass is at rest at time t=0, what should our beliefs be for spontaneous motion at any given later time?
For experts: nothing essential in the claim about induction depends on the details of the dome. We could use just about any indeterministic system. For example there are many Newtonian "supertask" systems that manifest spontaneous motions. Or, there is a simple recipe for making an indeterministic system. Take any theory with an interesting gauge freedom, i.e. one whose gauge degrees of freedom can change in time. Now declare that there is a factually true gauge. Since the signature of a gauge freedom is that the theory's equations fail to fix the gauge quantities, we now have an indeterministic theory in which future facts are not fixed by all past facts.
Before we tackle the case of the dome, let's look at a more familiar case in which everything goes pretty much as you'd expect. Indeed it looks very much like the dome, so a default supposition might well be that both deserve the same analysis. Consider a radioactive atom, which has a fairly short half life. The atom will just sit there doing nothing and then, without any immediate trigger, spontanously decay, just as the mass on the dome spontaneously moves.
The time at which the atom decays is governed by the law of radioactive decay. For present purposes, the one detail in it that we care about is that the law depends upon a time constant τ that is a distinctive property of each radioactive element. The time constant τ sets the overall time scale for the decay. A big τ means that we are likely to wait a long time before the decay happens. A small τ means that we are likely to wait a short time before the decay happens.
The precise formula that governs these times is this expression for P(t), the probability of decay sometime over time t:
P(t) = (1 - exp(-t/τ))
Plotting the probability P(t) against t gives this curve for the case of a time constant τ=1. When t is very small--say t = 0.1 = one tenth of τ--then the probability that decay has happened is small. Do the sums and it comes out at about 0.1. When t is large--say t = 5 = five times τ--the probability that decay has happened is large. Do the sums and it comes out at about 0.99.
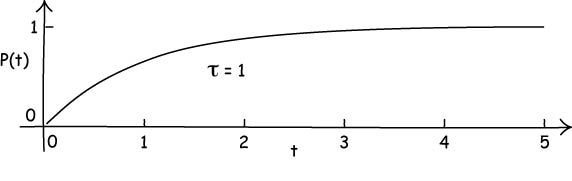
The time constant is closely related to the half-life of
the atom.
The half life t1/2=τ ln 2.
So now let's pose an inductive inference problem concerning this atom. We'll have an hypothesis H and evidence E:
E: At t=0, the atom has not decayed
H: The atom decays sometime in the ensuring time interval t.
The quantity we want is
[H|E] = the degree of support evidence E lends to hypothesis H
What should [H|E] be? This is a case covered by Lewis' "Principal Principle." We have physical chances, P(t). So our subjective propbabilities ought to match. That is, we would set
[H|E] = P(H|E) = P(t)
where the notation P(H|E) is a sort of hybrid notation that says that our degrees of support are probabilities.
Under this identification, our beliefs move in concert with the probabilities. For the case of τ=1 shown in the graph, we have little belief that the atom will decay in the first 0.1 units of time; but 0.99 belief that it will once 5 units have elapsed.
Consider the analogous inductive inference problem for the dome. We'll have an hypothesis H and evidence E:
E: At t=0, the mass is motionless at the apex.
H: The mass begins to move sometime in the ensuring time interval t.
What is the degree of support [H|E] that E lends to H?
Many find in the analysis of the radioactive decay of an atom a template that they cannot resist applying to the dome. The law of radioactive decay has an important property. It is the unique decay law that has a "no memory" property. If the atom has not decayed after 1 time unit, or 5 time units, or 10 time units, or whatever, then the probability of decay in the next unit of time always comes out to be the same. The atom does not remember how long it has been sitting, when the next time unit comes along.
That looks very promising. The distinctive thing about the physics of the dome is that it also has this "no memory" property. Whether the spontaneous motion happens at some moment is quite independent of how long the mass has been sitting at the apex. So why not set our degrees of support [H|E] equal to probabilities governed by the same formula as in the law of radioactive decay?
Why not? The reason is that time constant τ. Any instance of the law of radioactive decay has a time constant τ in it. And that time constant exercises a powerful influence on chance of the spontaneous event. To see this, here are graphs of P(t)=P(H|E) for values of τ=0.1, τ=1 and τ=10:
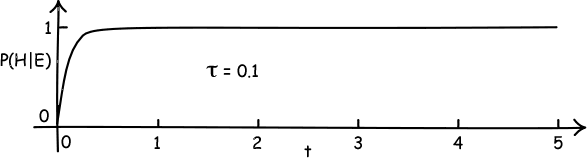
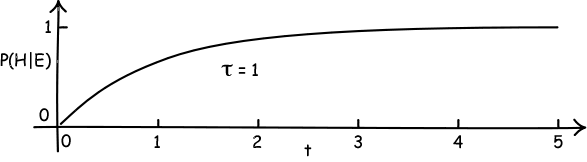
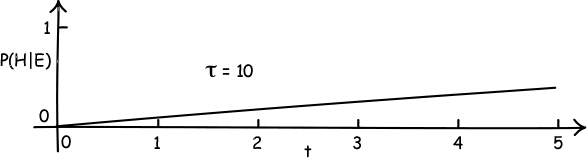
When τ is small, then we become near certain of the spontaneous event very soon, say within t=0 to t=1. If τ is large, then we expect to wait a long time before the spontaneous event occurs.
So what's the problem? Nothing in the physics of the dome fixes a time constant or any sort of time scale for the spontaneous motion of the mass. The physics is completely silent on how soon the motion may happen. It just says "it's possible." So if we are to use the probabilistic formula, we must add a time scale. The contradicts the basic spirit of the "Principal Principle" and the more general idea that the physics present should dictate the inductive logic. If we want to use the probabilistic law, we have to add more physical properties to the system than the system has. And that just seems wrong.
All we want to do is reason inductively about a system; we want to be inductive logicians. But somehow we have ended up as physicists, proposing new physical properties that the system--by construction--does not have.
Something has gone very wrong and, in my view, what has gone wrong is quite simple. We are trying to force the wrong inductive logic onto the dome.
There's a loophole I need to address. The probability formula of the law of radioactive decay is the unique probability law with the "no memory" property that the dome also has. So if any probability formula would work for the dome, that one would have to be the one.
Statisticians sometimes stretch the rules and use probability distributions that aren't really probability distibutions. One that could be used here is a uniform, improper distribution. It would assign the same small amount of probability ε to every unit time interval as shown in the graph below. It is "improper" since the probability assigned to all the unit time intervals taken together is not one, as the probability calculus demands, but it is infinity. While this seems a fatal problem, it turns out that if you are careful about how you use them, these improper distributions need not cause serious harm. But that is a topic for another place.
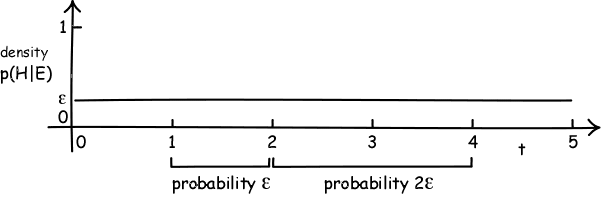
Tempting as this improper distribution may be, it suffers the same problem as the proper distribution. It still adds physical properties to the dome. For a consequence of it is that spontaneous motion in time t=1 to t=2 has probability ε and spontaneous motion in the time interval t=2 to t=4 is 2ε. Motion in the one interval is twice as probable--no more no less--than motion in the other. But nothing in the physics licenses this precise judgment. All the physics says is that motion in each interval is "possible"--and that is all.
Once again, we have passed from being inductive logicians to being physicists, adding more physical properties to the system than Newton's theory has already given it.
The probability calculus is the wrong calculus to use as an inductive logic for the dome. So what is the right one? How could we know? We've already seen how it can go in another case. Radioactive decay is governed by chances and we can let those chances pick out our inductive logic.
We can do exactly the same thing with the dome. However the physics of the dome is more impoverished than that of radioactive decay. So we are going to get a more impoverished logic. It is a somewhat mechanical exercise to read the relevant inductive logic from the physics. To do this, let's define
E: the mass is at rest at the apex of the dome at t=0.
H(t1,t2): The spontaneous motion happens in the time
interval t=t1 to t=t2,
where we write "(t1,t2)"
and shorthand for that interval of time. So H(10,20) just says that the
spontaneous motion happens sometime in t=10 to t=20.
Then we just take what the physics says and translate it into the logic using the same sort of transformations as we did in the case of radioactive decay. The chance of decay in t=5τ is 0.99; so our degree of belief in that decay is 0.99. However the indeterministic physics of the dome doesn't give us real valued degrees. It actually says rather little. It just says that a spontaneous motion in this or that time is possible. That's it. No degrees of possibility: not 50% possible, not 95% possible; and no comparative measures: not more possible, less possible, twice as possible. Just possible.
| What the physics says: | What it induces in the inductive logic: | ||
| The present state does not fix the future (indeterminism). The physics just tells us that a future state is necessary, possible or impossible. | The inductive logic for the support [A|B] of A from B has three values: nec, poss, imp. | ||
| If the motion happens in (10,20), then it necessarily happens in (0,100). | [ H(0,100) | H(10,20) ] = nec | ||
| Motion in any later non-zero interval is possible, given E: the mass is at
rest at the apex of the dome at t=0. |
[ H(0,10) | E ] = [ H(0,100) | E ] = [ H(10,20) | E ] = … = poss |
||
| If the motion happened in (0,10), it is impossible in (20,30). | [ H(20,30) | H(0,10) ] = imp |
The table gives a few obvious illustrations for a more general system. With a little reflection, you'll see that it is fully generated by a few simple rules. They are:
The complete inductive logic of the dome
[ A|B ]
= nec if B entails A
= imp if B entails not A
= poss otherwise
There is a common Bayesian rejoinder. While the strengths [A|B] of the inductive logic above are not conditional probability measures, we are just a few lines of mathematics away from conditional probability measures. Consider any probability measure at all that is adapted to the behaviors of the indeterministic systems through
P(A|B)
= 1, if B entails
A
= 0, if B entails
not A
and
0 < P(A|B) < 1 otherwise.
Every so adapted probability measure induces the logic of Section 5 by the rule
[ A|B ]
= nec, if
P(A|B) = 1
= imp, if
P(A|B) = 0
= poss, if
0 < P(A|B) < 1
Obviously there are other ways to define the logic of Section 5 in terms of probability measures; finding them is simply a challenge to our ingenuity.
Has this sort of possibility shown us that the probability calculus is the One True and Universal Inductive Logic after all? It has certainly not. The inductive logic of indeterministic systems are inherently non-additive. The degree of belief assigned to each of two mutually exclusive, contingent propositions is the same as the degree of belief assigned to their disjunction. If probability measures are to have any meaning as a logic of induction at all, their additivity is their essence. We add the numerical probabilities of two mutually exclusive outcomes to find the probabilities of their disjunction.
What the exercise above shows is that we can take one sort of inductive logic, one of additive measures, and use it to simulate another, with the non-additive degrees. Since the additive measures of probability theory are now offered as devices for generating all other logics, they have ceased to be used a logic in their own right. They have been reduced to a useful adjunct tool of computation and are no more the Universal Inductive Logic than is the differential calculus.
Of course we can readily simulate the additive measures of probability theory by other adjunct tools. A trivial example is provided by complex valued, multiplicative measures M, for which we replace the additivity axiom of probability by a multiplication axiom: for mutually exclusive outcomes A and B, M(AvB) = M(A).M(B). These multiplicative measures can simulate additive measures through the formula P(A) = log Re(M(A)), so these multiplicative measures can replicate any result achievable with additive measures. However that fact in no way makes these new measures the Universal Logic of Induction.
The discussion so far has sought to present an intractable problem for Bayesians of all varieties. Perhaps subjective Bayesians specifically have an escape. They hold that probabilities may be assigned subjectively, initially, but that as we conditionalize on new evidence, the whim of our individual opinions will be overwhelmed by the weight of evidence. Why cannot a subjective Bayesian assign a specific probability measure to the time of excitation? It merely represents that Bayesian’s opinion and makes no pretense of being grounded in the facts. Why does that fail?
First there is a general problem with subjective Bayesianism that is independent of this example. It changes the problem. Our original problem was to discern the bearing of evidence. That has been replaced by a different problem: to express one’s opinion, in such a way that eventually the bearing of evidence will overwhelm opinion.
Second, in the context of the present example, the subjective project fails by its own standards. The subjective approach can only be relevant to an analysis of the bearing of evidence if there is no way to separate out mere opinion from the objective bearing of evidence in the probability measures; and if we have some reason to think that mere opinion will eventually be overwhelmed by the weight of evidence. Neither obtain.
Here, the separation of whim and warrant can be effected. The three-valued inductive logic (3) expresses precisely what the evidence warrants. In so far as the probability assigned goes beyond, it expresses mere opinion. The translation from probability measures to the three valued inductive logic (5) enables us to read precisely how it goes beyond. Any probability that lies strictly between 0 and 1 merely encodes the value poss. Anything more, including the specific numerical value, is opinion.
There will also be the familiar probabilistic dynamics as we conditionalize on new evidence. However these changing probabilities do not represent shifts in inductive warrant. The new evidence will be the observation of whether the excitation happens in successive time intervals. In so far as the resulting shifts in probability assignments leave the probabilities strictly between 0 and 1, they amounts to pure shifts of opinion. If they force a probability assignment of 0 or 1, the shift is deductively generated, arising when the evidence deductively refutes or verifies the hypothesis.
That's it. That's the system whose inductive logic is non-probabilistic. Is it really that easy? I think so. The inductive logic appropriate to any system is determined by the facts prevailing in that system. The facts governing the dome call for a much simpler inductive logic than the probability calculus.
But you may have some nagging "yes, but..." worries. Let's look at two.
"That is all well and good, you say. The dome and other indeterministic systems require a different sort of inductive logic. Why should we care? Our world doesn't seem to have these sorts of indeterministic systems."
| That may well be the right thing to say when it comes to inferring inductively about systems in our world. However it does concede my main point. That--indeed, if--our world does not harbor such indeterministic systems is a factual matter. So what is being accepted is that the applicability of ordinary inductive logic depends upon certain facts about our world. That is what the material theory of induction claims; there is no universal inductive logic. | Compare with deductive logic, which has universal applicability. We quite happily apply deductive logic to weird systems like the dome. We don't say, "Oh that is a weird system, so modus ponens does not apply." Should not a truly universal inductive logic apply to weird systems as well? |
The sort of indeterminism without probabilities might well factually be the case for at least some processes in our world. Perhaps the simplest arises in standard big bang cosmology. Our cosmos emerged some 1010 and more years ago from a singularity in spacetime. We remain uncertain about whether that newborn cosmos came with enough matter to halt cosmic expansion and lead to a big crunch; or whether the density of matter was too small to halt the expansion, which will go on forever.
Standard cosmology tells us that many initial densities are possible, but it provides no probabilities for the different possibilities. It is a natural temptation to try to assign probabilities to the different values of matter density. However to do so would add to what the physics tells us.
Now that we know that our inductive logic depends upon at least some facts, are we so sure that the only pertinent facts are exotic ones like the absence of indeterministic systems? Might not other less exciting facts also be pertinent to our selection of the right inductive logic so that multiple inductive logics might well be appropriate to different domains in our ordinary experience?
Here's another "yes, but..." "All this is fine for inductive inference on physical systems whose properties are fully specified," you may say, "but why should that sort of thinking work in real inductive inference, that is, inductive inferences in which we have to deal with the uncertainties of the real world?"
I'm not moved by this worry. I do admit that the example is a little contrived. That was the price paid for an example in which we have complete control of all relevant facts that govern the ways that uncertainty enters into our analysis. For a complete control of those facts then makes it quite easy to see just which inductive logic is appropriate. In real world cases of inductive inference, those facts that govern the uncertainties are less clear to us. But that sort of muddiness seems no reason to me to think that things are any different. There still are facts governing our uncertainties and they will still dictate the appropriate logic.
It will, however, be harder for us to see precisely what that logic is because we are uncertain of the the pertinent facts. Indeed it all seems to be working out just as it should. In real world cases, we do struggle to see just which is the right inductive logic to be applied. That is just what you'd expect from the material theory of induction when we are unsure of the facts that govern the uncertainties. We routinely misdiagnose this problem, however, as our continuing failure to have lighted upon just the right universal logic of induction. The assured failure of our quest for this One True Logic of Induction in turn, it seems to me, go a long way in explaining why induction has perennially been such a murky topic.
Copyright John D. Norton. September 18, 2006; March 27, 2007; November 11, 2008.