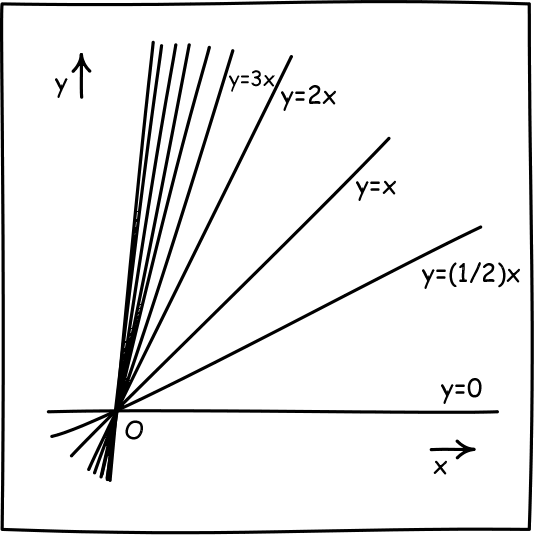How Did Einstein Think?
John D. Norton
Department of History and Philosophy of Science
and Center for Philosophy of Science
University of Pittsburgh
http://www.pitt.edu/~jdnorton
This page at http://www.pitt.edu/~jdnorton/Goodies
Prepared to accompany
cityLIVE! "everything einstein"
November 15, 2007, 6:30 pm
The New Hazlett Theater, Pittsburgh PA
Panelists: John D. Norton, Walter Isaacson
Moderator: Regina Schulte-Ladbeck
What is it...?
What is it about Einstein that we find so fascinating? One
side is that his thought and achievement seems so far above our mundane
sphere that we are inspired merely reflecting on him. There is a second side to this fascination. It lies, I believe, in
the thought that we are in the end not so far removed from him. While his
achievements are transcendent, he was in the end simply human. He ate soup
and paid taxes like the rest of us. He tried to keep ahead of the mundane
practicalities of life before they submerged him. He didn't wear socks and
thought just one soap for washing and shaving was quite enough.
It is that second sense that has always fascinated me. What
Einstein did, he did using tools available to all of us. He had no magic wand or secret subscription to Encyclopedia
Galactica, where all the truths of nature are written. He used tools and
methods available to everyone. He read the same text books and journals
available to every scientist of his day. His principal tool was a notepad
with a pen and pencil. He read and wrote and calculated and thought; and out
poured his extraordinary achievements.
In this regard, Einstein is part of an extraordinary tradition of achievement in science that extends to
antiquity. I am equally fascinated by the ancient astronomers. Look around
you. How could you figure out that the surface of the Earth is spherical--not
just curved, but a surface of constant curvature in all directions? The
ancient astronomers did it with nothing more than patient observation,
pointed sticks and ingenious thought. Well, perhaps I am a little more
fascinated with Einstein than the ancient astronomers.
My purpose here is to say something about how Einstein
worked and thought. I've written a lot elsewhere on the details of Einstein's
discoveries. Now I want to try to get behind them
and understand better the thinking that led Einstein to them.
Einstein's Answer
| What did Einstein have to say about his own
thinking? We have an answer. Jacques
Hadamard was a French mathematician who approached Einstein
with questions on Einstein's thought processes when Hadamard was
preparing a psychological survey on the internal mental worlds of
mathematicians.
Einstein's answer is reproduced more fully at right. It is
somewhat unrevealing. Einstein struggles
as would anyone trying to describe what transpires in their
consciousness. For example, to begin with, words and language do not
play any role in his thoughts. They must be sought for laboriously
later. This is an experience familiar to many of us who find our
thoughts racing ahead of our power to express them. It doesn't seem
to capture anything distinctive about Einstein's thinking.
|
Perhaps we should heed Einstein's
advice:
"If you want to find out anything from the theoretical physicist about the
methods they use, I advise you to stick closely to one principle: don't
listen to their words, fix your attention on their deeds."
"On the Methods of Theoretical Physics," Herbert Spenser Lecture, Oxford,
June 10, 1933.
What can we learn about Einstein's thoughts and methods by looking at his
work? I'll sharpen my queries in a series of questions that span from the
general and big to the narrow and specific.
Inscrutable Flash of Insight
or
Systematic exploration?
Let us start with the biggest question
first. When Einstein made his big discoveries, how did they happen?
Did they come in momentary flashes of insight, the product of hidden
processes that suddenly flood the mind with their perfected insight? Or did
they come through slow labor, much as we might build a tall tower by
patiently and systematically piling the bricks one upon another?
Einstein's major discoveries seem to have both in them. Let
us consider two discoveries.
Special
Relativity
Take Einstein's 1905 discovery of the special
theory of relativity. This is the theory for which he is best
known. It says that moving rods shrink, moving clocks slow and that
the speed of light is a fundamental barrier through which nothing can
accelerate.
The decisive moment in the discovery of the theory came after
Einstein had become convinced of two apparently
contradictory results. One was the principle of relativity
that tells us that uniform motion has no effect on physical systems.
The second--soon to be called the light postulate--asserted that the
speed of light always came out to be the same number, 186,000 miles
per second. How could he have both? If we chase after a beam of
light, surely we must judge it slow down?
The decisive insight, Einstein later recalled, came after a visit
with his friend Michele Besso, when the two discussed his work. Both
are possible, Einstein realized, if we give up an assumption about
simultaneity. We had assumed that whether two events at different
places are simultaneous is an absolute fact. It is not, Einstein now
saw. Observers in relative motion will disagree on whether two events are simultaneous.
What if those events are used to time how fast light goes, say how
long it needs to traverse some measuring rod? Then those differing
judgments of simultaneity will make the seemingly impossible, possible. The original observer and
the one chasing after light will both judge the light to have the
same speed. The rest was mechanical. Einstein needed only 5 to 6
weeks to write what is now often singled out as the greatest
scientific paper of the 20th century, "On the Electrodynamics of
Moving Bodies."
So it was all in that moment? Hardly. The real work lay in the
reflections that convinced Einstein of the two apparently
contradictory commitments. That work took, by Einstein's own
reckoning, seven and more years. From his student days, Einstein had
been fascinated by the latest, hottest theory of the moment, Maxwell's electrodynamics. It is a theory of
electricity, magnetism and the waves that propagate in these fields;
it was the closest the time had come to a theory of everything. One
of its most striking results was that light is just a wave of
propagating electric and magnetic fields and that it has a single,
definite speed, 186,000 miles per second.
Maxwell's theory was based on an ether with a preferred state of
rest. The problem Einstein found was a tension between this preferred
state of rest and the failure of experiments to reveal it. Worse on
his reading the theory seemed to predict that no experiment could
reveal it. So Einstein pursued the only line of research that seemed
promising, attempts to modify Maxwell's
theory in a way that would do away with the ether state of rest. It
was a long and systematic search that went nowhere. The more he
tried, the worse it got.
Einstein came to a crisis. All efforts
to modify Maxwell's electrodynamics had failed. But how could he keep
both the idea that there is no ether state of rest and also the
celebrated result of Maxwell's theory that light travels at exactly
186,000 miles per second. Then an observer chasing a light beam would
not find the light to slow.
These long efforts prepared the ground for Einstein's celebrated
visit to Michele Besso.
|
General Relativity
We see this same mix of flash of insight and systematic
construction in the case of Einstein's greatest discovery, the
general theory of relativity. This is the theory that tells us that
gravity is just a curvature of the
geometry of spacetime. It tells us that the real geometry of
space is not the one Euclid described millennia ago and opens the
door for later researchers to posit black holes and other
extraordinary pathologies of space and time.
The flash came in Einstein's first step. In 1907, while still a
patent clerk, he was pondering how one might produce a relativistic
theory of gravity and he was not having much success. Then he was
struck by the fact that an observer in free fall no longer feels his
own weight. He then hit upon what he called "the
happiest thought of my life." One can produce gravity in
gravity free space merely by reversing the process. Acceleration
creates a gravitational field. This is his "principle of
equivalence."
That thought was the first step. It took seven and more years for
Einstein to complete this work in 1915. Its first phase was devoted
to systematic constructions that derived
directly from Einstein's "happiest thought." In it, acceleration
produced a special case of a relativistic gravitational field.
Einstein now turned to the task of cataloguing the properties of this
special case and generalizing them to arrive at a more general
theory. In the special case, clocks are slowed and light is deflected
by the gravitational field, which is proportional to the a variable
speed of light. Those properties, Einstein supposed, hold in all
static gravitational fields and he could arrive at the description of
these fields merely by slightly generalizing the ways that the speed
of light could vary with position in space.
These constructions occupied Einstein's efforts in gravitation
theory up to mid 1912. In the year that followed, Einstein made the
transition to a spacetime theory in which gravitation is related to
the curvature of its geometry.
Unlike the case of special relativity, we have been able to
reconstruct in some detail the steps and missteps of this decisive
advance. We have a series of publications documenting the various
stages of the developing theory and even his private notebook calculations, which I have
spent a great deal of time in reconstructing. Einstein's explorations
went quickly and slowly, straight and meandering. At times they
became almost recipe-like. Einstein laid out the requirements his
final equations must meet and then systematically searched for
equations that satisfied them.
While Einstein was launched by a flash of insight, the greatest
part of work on the theory was spent in this systematic exploration.
That eventually brought his project to completion.
|
Unfettered Speculation
or
Controlled Flight?
Einstein did have decisive flashes of inspiration. What was
their character? Were they just wild moments of unfettered speculation? Or
were they controlled? The first fits with the image of Einstein's scientific
creativity as resulting from a liberation from
reason. The second fits with it as a more profound fulfillment of
reason.
My view is that his flights fit much better with the
second. In the two cases we have just seen, the moment of inspiration was
seeded by earlier work and directly responded to
it.
The insight over the relativity of
simultaneity came after years of struggle with failed efforts to
reconcile the principle of relativity with Maxwell's electrodynamics. He did
not so much choose to leap into the unknown as he was pushed by the
accumulated pressure of those problems.
Things were similar but not so acute with the "happiest
thought of [his] life," the principle of
equivalence. It emerged after a series of failed attempts at finding a
relativistic theory of gravitation. All the candidates he thought up failed
to fit a simple expectation about gravity that he traced back to Galileo: all
things big and small must fall with the same acceleration. The virtue of the
gravitational field created by acceleration was that it was assured to have
exactly this property.
| We find the same control in another
of Einstein's legendary leaps.
In 1905, in the first of his papers of his annus mirabilis,
Einstein proposed that light energy might not be distributed over
space, as the wave theory supposed. Rather the energy of high
frequency radiation was localized into
pointlike quanta whose positions in space are independent of one
another, rather like the molecules of an ideal gas.
The idea was quite extraordinary. The great achievement of nineteenth
century physics had been Maxwell's electrodynamics and its proudest
moment had come when it had shown that light was merely an
electromagnetic wave. As the twentieth century began, no result seemed more secure than the wave
character of light. Yet here was Einstein contradicting it.
Did a departure this radical result from unfettered speculation that
yielded some blinding flash of insight? How else could it arise? We
have no autobiographical recollections from Einstein on the moment at
which he hit upon this remarkable idea. However we do have plenty of
clues from his published papers over how he might have arrived at it.
All those clues (surveyed at right) point to "controlled flight."
|
Thinking Mathematically
or
Thinking Physically?
What sort of theorist was Einstein? Everyone knows that he
brought profound insight in the form of new theories in mathematical physics.
If we seek the origin of that thought, should we
put the emphasis on the "mathematical" or the "physical"? The distinction
between the two is one that Einstein himself drew and reflected upon.
In thinking mathematically, or,
as Einstein's sometimes said, formally, one takes the mathematical equations
of the theory as a starting point. The hope is that by writing down the
simplest mathematical equations that are applicable to the physical system at
hand, one arrives at the true laws. The idea is that mathematics has its own
inner intelligence, so that once the right mathematics is found, the physical
problems melt away. Philosophers will recognize this as a form of
Platonism.
In thinking physically, one
proceeds quite differently. The starting point is physical. Perhaps it lies
in an examination of the results of experiments; or in an insistence on
certain founding physical principles, like the principle of relativity of the
conservation of energy and momentum; or perhaps it draws on deeper, more
visceral ideas of what can and cannot happen in real physical situations.
Einstein's theories sometimes made special mathematical
demands on physicists. His great achievement, the general theory of
relativity, required physicists to learn what we now call "tensor calculus,"
which proved something many found formidable. But it was
not mathematics that drove Einstein's theoretical successes.
Einstein's enduring achievements in physics were virtually
all a product of the earlier part of his life: special relativity, Brownian
motion that shows the reality of atoms, the light quantum, general
relativity, the "A and B" coefficients paper that grounds lasers. All this
was done before he turned 40. Virtually all of these achievements depended
upon a very astute form of physical thinking.
Einstein then dressed it in mathematical clothing, seeking where ever
possible to keep the mathematics as simple as he could.
Just how did Einstein's physical insight work? One part was
an keen instinct as to which among the flood of experimental reports were
truly revealing. Another was his masterful use of thought experiments. Through them Einstein could cut
away the distracting clutter and lay bare a core physical insight in
profoundly simple and powerfully convincing form.
Here's an example of a thought experiment from Einstein's
work on general relativity already mentioned above. Einstein realized at the
start that we needed to think differently about
the empty space of special relativity if we were to arrive at an acceptable
relativistic theory of gravity. We needed to stop thinking of it as the
gravitation free case. It is actually the simplest case of a gravitational
spacetime. His claim, the principle of equivalence, was that uniform
acceleration in empty space produces a gravitational field.
But how can that be made intelligible? Einstein's approach
was simple and ingenious. He had us to imagine a physicist who is drugged and
placed inside a box. That box is transported to a
distant part of space where it is accelerated uniformly by some agent. The
phyicist wakes up. Any object released by the physicist would accelerate to
one part of the box. The acceleration would be the same for all objects
released, be they small or large in mass. That is the distinctive property of
gravity: it accelerates all masses alike. Could the physicist know that the
box is accelerated unformly in space and not at rest in a homogenous
gravitational field? No, Einstein asserted, there is no way. There is no
difference between the two cases. The result of the acceleration is to create
a gravitational field inside the box.
Einstein himself recognized this special
facility for physical thinking when he wrote his Autobiographical
Notes (see right), reporting that this physical insight and
intuition outstripped his mathematical
instincts.
There is, however, a unexpected ending to the story that also
surfaces in these remarks. Einstein's general theory of relativity
derived essentially from physical
thinking. How could he devise a theory of gravity that frees us from
our dependence on any special coordinate systems? How could
acceleration be deprived of its absoluteness in such a theory?
However the theory grew so complicated and difficult that
Einstein's physical instincts failed him at the crucial moment. In
1913 he published a defective version of the theory. After nearly three years of hesitation and doubt, he
was able to repair the theory by writing down the mathematically
simplest equations. They were ones he'd nearly adopted three years
before. He had then thought them to be inadmissible for physical
reasons. The diagnosis of his earlier error was clear. He had
mistakenly trusted his physical insight over mathematical
simplicity.
|
| The experience triggered a profound change in Einstein's thinking. He now became
convinced that the path to a deeper understanding of the physical
world lay in mathematics.
Einstein's conversion is expressed most eloquently in his own
words from a lecture given in 1933 (left).
Here Einstein has adopted a form of Platonism. What makes his adoption of it
extraordinary is that he believed it was a lesson learned from his
own experience of physical theorizing.
|
Geometric
or
Algebraic Thinking?
Einstein's work continued to depend on mathematics and the
mathematics he employed grew more as time passed. There are different ways of using mathematics to clothe a theory
and Einstein adopted a particular stance towards them. The two ways I will
describe will be recognized by anyone who has had a high school exposure to
mathematics.
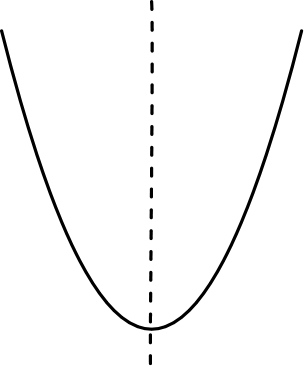
| One approach is geometrical. The most familiar expression of it
is Euclid's geometry. We pursue geometrical structures there by
drawing lines and curves and seeing how they intersect. Take a
parabola, for example. Does it have mirror symmetry about the
vertical axis shown at right as a dotted line? To check, we have to
find out whether flipping the figure over the dotted line makes a
difference. It does not change the curve at all, so we infer that the
parabola does indeed display this mirror symmetry. |
 |
Another approach is algebraic.
This is a way of doing mathematics that concentrates on writing symbolic
expressions and manipulating them. "A fish is 10 inches long plus half of
itself. How long is the fish?" We say. "Let x be the length of the fish. Then
x = 10 + x/2. Solving, we find x=20. The fish is 20 inches long."
Here's another problem. Take the formula y=x2. Is it
changed when we replace x by -x? A quick calculation shows that it is not.
y=x2 becomes y=(-x)2 which is just y=x2
again since (-x)2 = x2.
This last problem is purely one of symbolic algebraic
manipulation. Yet it is really just the same the
problem as the symmetry of the parabola. If x and y are ordinary
Cartesian coordinates the y=x2 is the formula for a parabola.
Replacing x by -x is just the operation of reflection over the y axis. So
when the formula y=x2 stays the same under this transformation, we
have the algebraic equivalent of the demonstration of the mirror symmetry of
the parabola.
We see the difference of approach expressed directly in
physics. Consider special relativity. Most treatments of the theory rapidly
seek to develop the notion of spacetime. Through it one learns a wonderfully
simple way to conceive the theory. All of space and time taken together form
a single spacetime. Special relativity is really
just the theory of this spacetime's geometry. One uses the theory by drawing
straight lines and hyperbolas and forming geometric constructions similar to
those we learned in elementary geometry classes. The principle of relativity
is expressed as a sort of isotropy of the spacetime, somewhat akin the
isotropy of a Euclidean space--that all its directions are the same.
That geometrical way of conceiving special relativity is
not Einstein's. It was devised by the mathematician Hermann Minkowski shortly
after Einstein published his special theory of relativity. Einstein was reluctant to adopt Minkowski's method,
thinking it smacked of "superfluous learnedness." It was only well after many
others had adopted Minkowski's methods that Einstein capitulated and began to
use them. It was a good choice. It proved to be an essential step on the road
to general relativity.
Einstein preferred to think of his theory in terms of the
coordinates of space and time: x, y, z and t. The essential ideas of the
theory were conveyed by the algebraic properties
of these quantities, treated as variables in equations. Its basic equations
are the Lorentz transformation, which, in Einstein's hands, is a rule for
changing the variables used to describe the physical system at hand.
The laws of physics are written as symbolic formulae that
include these coordinate variables. The principle of
relativity of relativity then became for Einstein an assertion about
the algebraic properties of these formulae; that is, the formulae stay the
same whenever we carry out the symbolic manipulation of change of variables
of the Lorentz transformation.
The emphasis in Einstein's
algebraic approach is on variables, not spacetime coordinates, and formulae
written using those variable, not geometrical figures in spacetime.
For many purposes, it makes no difference which approach
one uses, geometric or algebraic. Sometimes one is more useful or simpler than the other. Very often, both
approaches lead us to make exactly the same calculations. We just talk a
little differently about them.
However there can be a big difference if we disagree over
which approach is more fundamental. We now tend
to think of the geometric conception as the more fundamental one and that
Einstein's algebraic formulae are merely convenient instruments for getting
to the geometrical properties.
There is some evidence that Einstein
saw things the other way round. He understood the geometric
conception, but took the algebraic formulation to be more fundamental. A
simple example illustrates how this difference can matter a lot.
Take a two dimensional Euclidean space with some
origin point O. We will consider all the
straight lines that pass through it. An elementary fact of
Euclidean geometry is that all these lines are exactly the same. None
is special geometrically.
There is another way to investigate the geometry of a Euclidean space
and the lines in it. That is to label all its points with
coordinates. We usually use x and y and label the origin point O with
the values x=0 and y=0. Then a straight line through the origin O is
given algebraically by the formula
"y=mx," where m can have any real value. |
 |
|
|
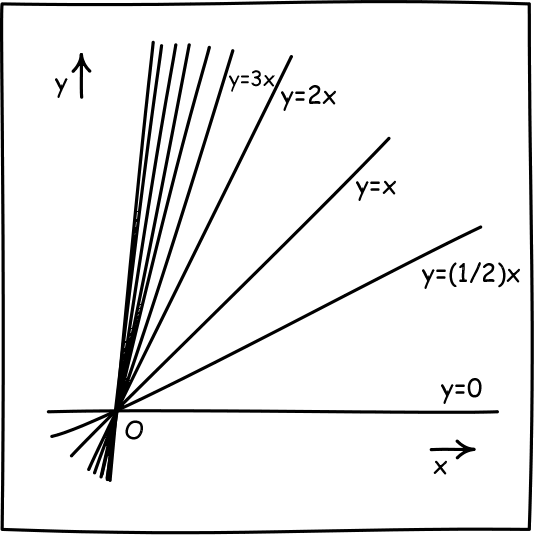 |
So consider the sequence of formulae generated as
m varies:
y=0,
y= (1/2)x,
y=2x,
y=3x,
y=4x,
...
and so on. As m gets bigger, the straight lines described get closer
and closer to a vertical line through O.
Our geometric intuitions tell us that this is where the sequence of
formulae must be heading.
But they do not go there. When m gets to be infinitely big, we get
the formula "y=infinity." It not at all
clear what that represents. It is not a line passing through O since
all lines passing through O must pass through x=0, y=0. These values
do not satisfy the formula "y=infinity."
|
One could take two attitudes to this little oddness. One
could think geometrically. One could say that
what we are really talking about are just straight lines in Euclidean space.
So the limit of the sequence is just a vertical line. What has gone wrong is
that algebraic device for representing lines as formulae has "gone bad" in
this limiting case. So we shrug the whole thing off as an inadequacy in the
algebraic representation.
One might also think
algebraically and take the formulae to be fundamental. Then one would
say that the set of structures represented themselves go bad in the limit.
That is, they are "singular" to use the fancier term when infinities like
this appear. That amounts to saying that something odd is afoot as we
approach the limit of the sequence.
| We would probably now choose to think
geometrically. There is clear evidence that Einstein thought algebraically about these
cases. This case of straight lines is a simple one I concocted as an
illustration. Einstein never spoke of it. There are, however, more
complicated cases in which Einstein clearly favored the algebraic
representation with its singularities over the regular geometric
representation.
|
One arose in the later 1910s shortly after the birth of
relativistic cosmology. Einstein became engaged in a dispute with de Sitter and others over a new cosmological spacetime
explored by de Sitter.
| In geometrical terms, the de Sitter spacetime is a
hyperboloid of revolution in a five dimensional Minkowski spacetime.
Fortunately, this somewhat intimidating technical specification is
not needed to understand the essential point. De Sitter spacetime is
completely homogeneous. Every point is
geometrically just like every other. It also has no matter in it. |
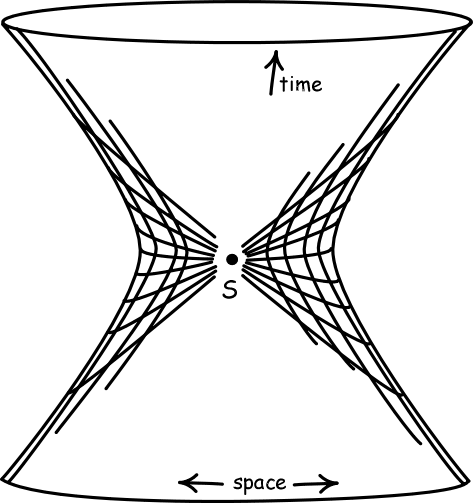 |
As usual, Einstein used coordinate labels to
describe the properties of this spacetime. The coordinate system he
used, however, had the awkward property of not covering the surface
properly. It left some parts out and, worse, "went bad" on an entire spherical surface
enclosing the region coordinatized.
In the figure at left, the coordinate
system "goes bad" at the point marked S where the spatial coordinate
lines cross. If the figure included all the three dimensions of
space, this point would be the surface of a sphere.
|
Thinking geometrically, we
would just say that there is no pathology on this surface. It is just that
our coordinates used to describe the surface at those points are not working
well any more. How could it be otherwise, we might wonder, since all points
in the spacetime are the same geometrically.
| Einstein did not say this. He took the algebraic structures arising from this
coordinatization to be fundamental and insisted that there is a
singularity in the spacetime on this sphere. He used a computation by
the mathematician Hermann Weyl to suggest that the singularity
somehow harbored masses that would act like gravitational source
masses for the whole spacetime. |
For Einstein, the algebra trumped the geometry and he found
pathologies where we now think there are none.
In Sum
The transcendent achievement of
Einstein required many components. He needed an intellect with singular
powers. He needed a dedication to hard work. And he needed a commitment to
finding the right answer, no matter how hard the path became.
We can learn just a little more from this glimpse of how
Einstein thought. For Einstein had quite particular strengths. They lay in an acute physical intuition that
guided him to the fertile physical ideas and revealing experimental results.
As long as Einstein used those particular skills to drive his work, he
produced one great success after another. He was the right thinker, with the
right abilities, in the right place and time.
Then Einstein changed his
thinking. He was no longer guided so much by physical intuition as by
mathematical simplicity. As that change set in, Einstein's work began to
languish. He retreated more and more into a private world in which he spent
decades searching for his unified field theory. While he did that, the
mainstream of physics moved on to elaborate the quantum theory. Einstein did
not follow. His physical instincts told him that this was not the fundamental
theory; that was to be found by the mathematical path.
We might lament that Einstein's work took this pathway.
What might have happened had he continued to
follow his older methods? We cannot know. However I suspect that not much
would have emerged. Einstein's physical instincts were the ones needed to
develop relativity theory and his other successes.
When the focus of research moved to quantum theory, a
different sort of instinct seemed to be required. That was embodied by the
Danish physicist Niels Bohr. He had a
characteristic tolerance and even delight in contradiction. That
characteristic enabled Bohr to theorize successfully in the bewildering and
uncertain quantum domain and in a way that Einstein's physical sensibilities
found repugnant. Einstein's role changed to that of a senior sage, warning
the new generations of the dangers of the path they had chosen.
Copyright John D. Norton. November 12, 16 2007.