Atoms Entropy Quanta
Einstein's Statistical Physics of 1905
John D. Norton
Department of History and Philosophy of Science, University of Pittsburgh
Pittsburgh PA 15260. Homepage: www.pitt.edu/~jdnorton
This page (with animated figures) is available at www.pitt.edu/~jdnorton/goodies
Einstein's work in statistical physics of 1905 is unified
by a single insight: Physical systems that consist of many, spatially localized, independent micro-components
have distinctive macro-properties. These macro-properties provide a signature
that reveals the system's microscopic nature. Einstein used this insight in
two ways. It enabled him to treat many, apparently distinct systems alike,
simply because their micro-components are localized and independent. And he
used the measurable macro-signature to reveal the micro-constitution of
physical systems. In the case of heat radiation, the result was
revolutionary.
1. The Three Statistical Papers of 1905
In his annus mirabilis of 1905, Einstein published
three papers in statistical physics that appeared to be only loosely
connected. They were:
Einstein's doctoral dissertation
"A New Determination of Molecular Dimensions"
Buchdruckerei K. J. Wyss, Bern, 1905. (30 April
1905)
Also: Annalen der Physik, 19(1906), pp. 289-305.
Einstein used known physical properties of sugar solution (viscosity,
diffusion) to determine the size of sugar molecules.
"Brownian motion paper."
"On the motion of small particles suspended in liquids at rest required by
the molecular-kinetic theory of heat."
Annalen der Physik, 17(1905), pp.
549-560.(May 1905; received 11 May 1905)
Einstein predicted that the thermal energy of small particles would manifest
as a jiggling motion, visible under the microscope.
"Light quantum/photoelectric effect paper"
"On a heuristic viewpoint concerning the production and transformation of
light."
Annalen der Physik, 17(1905), pp.
132-148.(17 March 1905)
Einstein inferred from the thermal properties of high frequency heat
radiation that it behaves thermodynamically as if constituted of spatially
localized, independent quanta of energy.
These three papers were intimately connected by a single insight that Einstein used and
developed as the content of the papers unfolded. Take a system that consists
of very many, spatially localized, independent microscopic components. That
constitution can be read from the thermal properties of the system, as long
as one knows how to read the signs. The most familiar example is a very
dilute kinetic gas; its component molecules move independently. This
constitution is directly expressed in the fact that the pressure, temperature
and volume of the gas conforms to the ideal gas law.
Einstein was not the first to see these sort of
possibilities. However he used them with greater fluidity and reach than ever
before.
2. A Mini-Tutorial on Ideal Gases
For a very gentle warm up exercise, see "How big is an atom?"
To illustrate this insight, let us look at this most
familiar case of ideal gases. This is the case of most ordinary gases, just
like the air, when they are at ordinary temperatures that are not too cold
and pressures that are not too high, so that they remain very dilute.
|
 |
|
Here is an ideal gas trapped in a cylinder by a weighted piston.
That it obeys the ideal gas law means
that the following calculation always works.
Take the pressure P and
multiply it by the volume V of
the gas. Whatever you get will always be exactly the same as what you
get when you take the number of
molecules n, multiply it by Boltzmann's constant k and the temperature T.
Or, to put it more simply:
PV = nkT |
|
This result is so simple that it is easy to miss what is
quite remarkable about it. What is remarkable is
exactly that it is so simple. Gases come in many different forms. We might
have a very light gas like helium, the gas used to lift balloons, whose
molecules are little spheres. Or we might have a denser gas like the oxygen
of the air, whose molecules are dumbbell shaped. Or we might have a vaporized
liquid, like water vapor, whose molecules are shaped something like little
Mickey Mouse heads. In every case, the same law holds, even if the oxygen or
water vapor are mixed up with another gas like nitrogen in the air. Yet
nothing in the law takes note of all these differences. All that enters the
law are the the volume, the temperature, the number of molecules and a single
universal constant, Boltzmann's constant k. From them, using a little easy
arithmetic, the law tells you what the gas pressure P will be.
How can the ideal gas law do this? It can do it because the
truth of the law does not depend upon the
detailed physical properties of the gas. Rather it depends only on a single
fact shared by all dilute gases: they consist of may independent spatially
localized molecules. The law needs this and nothing more; as a result it does
not need to ask if the gas molecules are heavy or light, this shape or that;
or even if the molecules are alone in space or surrounded by molecules of
another type. This fact also foreshadows the far broader application of the
ideal gas law than just to ideal gases.
Exactly how this law comes
about is a somewhat technical issue, although not that technical. In
its very simplest form it goes like this. The single most important result of
the statistical physics of Maxwell and Boltzmann for a thermal systems is
that the probability that one of its molecules is in some state is fixed by
that state's energy. Specifically, the probability of a state with energy E
is proportional to an exponential factor exp(-E/kT). So, for the gas in the
above cylinder, we can ask for the probability that one of its molecules will
be found at some height h. Now its energy at height h is its energy of motion
plus the energy of height, mgh, where m is the molecule's mass and g the
acceleration of gravity. This formula assumes the essential thing, that the
molecules are independent of each other. For the energy of the molecule
depends on its height and not on the position of any other molecules.
What this means is that the probability of finding some given molecule at height h
decays exponentially with height h according to the factor exp(-mgh/kT). Now
the gas is more dense where there are more molecules; or more precisely, the
probability of finding a molecule at height h is proportional to the density
of the gas at height h. Therefore the density of the gas decays exponentially
with height according to the same factor exp(-mgh/kT). So this means that the
gas is more dense lower down and less dense higher up.
|
 |
|
All that seems reasonable enough. But you might also quite
reasonably ask why the force of gravity
just doesn't pull all the gas molecules down to the bottom of the
cylinder, so that they lie in a big heap at the bottom of the
cylinder, like a pile of dust. The simple answer looks at the gas
microscopically and calls upon the thermal motions of the molecules
to scatter them through the chamber. The relevant effect of these
microscopic motions can be redescribed macroscopically as a pressure.
The many microscopic collisions of the molecules with the piston, for
example, appear macroscopically as a smooth pressure exerted by the
gas on it. |
|
Correspondingly the tendency of the gas to scatter upward
because of the microscopic motions appears macroscopically as a pressure
gradient in the gas. There is a higher pressure lower in the cylinder and
that higher pressure tends to push the gas upward. Now different pressure
gradients in the gas will lead to different density distributions, with
equilibrium arising when the pressure gradient exactly balances the weight of
the gas and piston above. Which pressure gradient
will lead to a distribution proportional to exp(-mgh/kT) in every case?
Well--you know the answer. It is exactly the pressure gradient given by the
ideal gas law, PV=nkT!
To summarize, the assumption
that a gas consists of many, independent, localized molecules leads to the
ideal gas law. And it should come as no surprise that the argumentation can
be reversed. If we have any gas in the context of Maxwell-Boltzmann
statistical physics that satisfies the ideal gas law, then it consists of
many, independent molecules.
There remains one subtle point that will become of central importance. The ideal gas law
follows from the assumption that the gas consists of many, independent,
localized molecules. Notice what is not assumed. It is not assumed that the
molecules move in straight lines at uniform speed between collisions with
other molecules; or that the molecules are the only matter present. The ideal
gas law is a much more general result. It holds for any thermal system
consisting of many, independent, localized components; and the notion of
component and its context can be quite broad.
All this can be made precise mathematically with only a
little more effort. See how here.
3. Einstein's Doctoral Dissertation
Of his statistical papers on 1905, the light quantum paper
was published first. However in terms of the development of their ideas,
Einstein's doctoral dissertation presents the natural
starting point. The common ideas of the three papers appear in it in
their simplest form and they are developed adventurously in the other two
papers.
The point of Einstein's
doctoral dissertation, "A New Determination of Molecular Dimensions," was
clearly stated in its title. It was to determine how large molecules are. The
answer was given in a particular way. A basic result of chemical atomism is
that there are always the same number of molecules in one gram mole of any
substances--such as 2g of hydrogen gas, or 18g of water, or 32g of oxygen
gas. That number is N. It is called Avogadro's number in the English
tradition and Loschmidt's number in Einstein's German tradition. Finding N
then automatically tells us the mass of hydrogen molecules, water molecules
and oxygen molecules.
The method Einstein hit upon was simple in conception. Pure water has a certain
viscosity that measures how readily it flows. Water's viscosity is very much
less than honey, for example, which flows much less readily. The addition of
sugar to water to make a syrup like honey increases the viscosity. Einstein
proposed that, at least in the case of dilute sugar solutions, the increase
in viscosity is simply due to the bulk of the sugar molecules obstructing the
free flow of the dissolving water. Einstein's project was to model this
obstructive effect as a mathematical problem in fluid flow; and to compare
the results with experimentally determined viscosities of dilute sugar
solutions; and thereby to estimate N. The idea was simple, but its execution
was not.
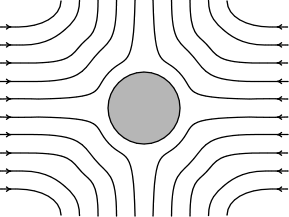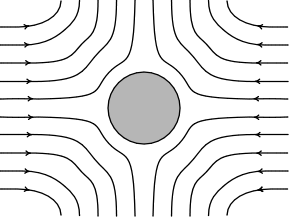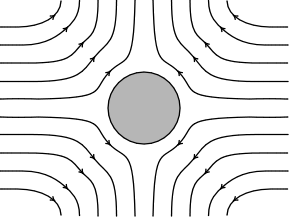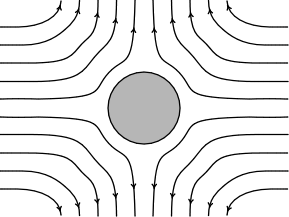 |
Einstein managed to reduce the problem
to computing the flow that results in the situation shown opposite.
Water flows inward on one axis and then diverges outward on others.
That flow will be impeded by the presence of a sugar molecule at the
center, where the molecule is presumed to be a perfect sphere. That
impeding of the flow, Einstein assumed, would manifest as an increase
in the viscosity of the solution. |
After a long and hard
calculation, after Einstein had made many special assumptions just so
that the computation could be done at all, Einstein arrived at his result.
The apparent viscosity mu of the water was increased to mu* of the
solution in direct relation to the fraction of the volume phi of the solution
taken up by the sugar:
(1) mu* = mu . (1 + phi)
And the fraction of the volume taken up by the sugar could be determined by
simple geometry from rho the sugar density, m the molecular weight of the
sugar, P the radius of the sugar molecule and N:
(2) phi = (rho/m) . N . (4pi/3) . P3
Well, it was a little more complicated.
Einstein made an error in the calculation and the correct result was
mu* = mu . (1 + (5/2)phi). The examiners did not notice. Einstein
was awarded his PhD and years later corrected the mistake.
Don't be put off by all the
terms in equations (1) and (2). All that really matters is that Einstein has
equations that relate things that can be measured (viscosity of sugar
solutions, etc.) to the thing he wants to know N. So Einstein could take
equations (1) and (2), combine them and turn the outcome inside out. The
result is
(3) N = (3m/4 pi rho) . (mu*/mu) .
1/P3
Or, if we express it in terms that matter:
(3) N = (things that
can be measured) x 1/P3
|
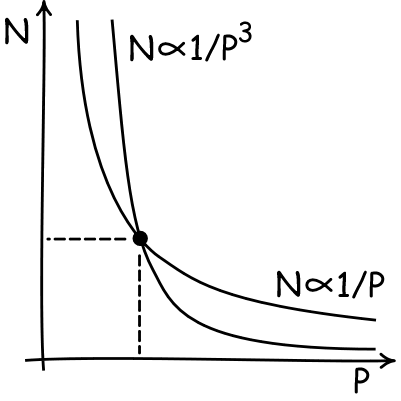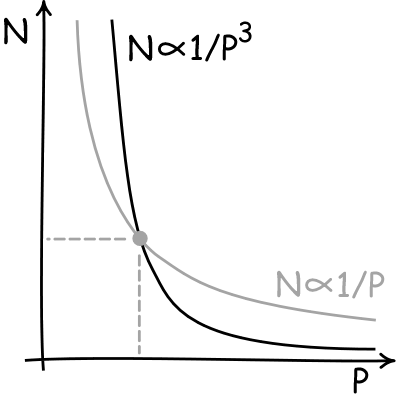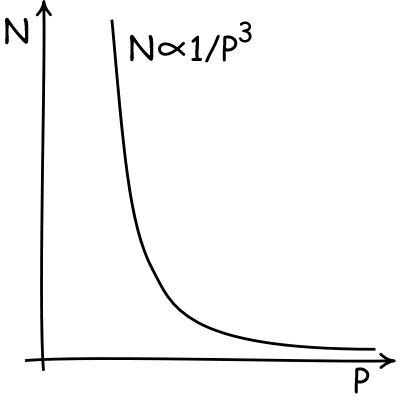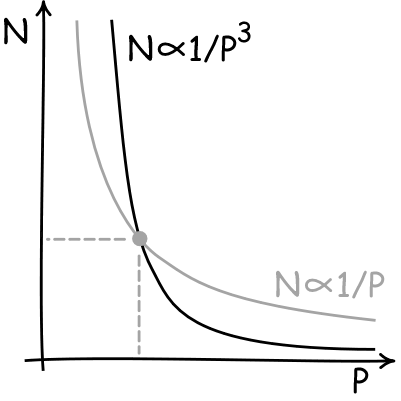 |
|
You'll immediately see the problem with equation (3). N and the
radius of the sugar molecule P are both things that we don't know
(and want to know). So Einstein has that old foe of algebra homework:
ONE equation in TWO unknowns. And we all
learned in school that you cannot solve that. In effect we have a
rule such that if we know the value of one unknown--P say-- we can
figure out the other--in this case N. That is shown in the plot. We
have a curve that displays all the values of P and the corresponding
values of N that go with them.
What Einstein needed was a second equation, so he would have TWO
equations in TWO unknowns. Then he would have a second curve on the
plot and where the two curves crossed he would find the unique values
of both N and P. |
|
But where could Einstein get
his second equation? He found it by looking at how sugar diffuses in water.
How he analyzed this diffusion process will be our real focus. So let me just
state his result for the moment. It uses the diffusion coefficient D that
determines how fast sugar diffuses and is measurable directly in experiment,
and the ideal gas constant R.
(4) N= (RT/6 pi mu D) . 1/P
or in terms of what matters
(4) N = (things that
can be measured) x 1/P
So Einstein now had two equations (3) and (4) in his two unknowns, N and P,
and they could be solved. He found N = 2.1 x 1023. Later, after he corrected his calculation for his
error, he had N = 6.6 x 1023, which is much closer to the modern
value of 6.02 x 1023.
4. The Statistical Physics of Dilute Sugar
Solutions
Diffusion is a familiar process. The smell of last nights
pepperoni pizza soon fills the refrigerator as the aroma diffuses into every
corner. Similarly a spoonful of sugar syrup carefully placed at the bottom of
a cup of water (and not stirred!) will slowly diffuse over a period of days
and weeks through the water making a (roughly) uniform sugar solution. The
microscopic mechanism of diffusion is simply the
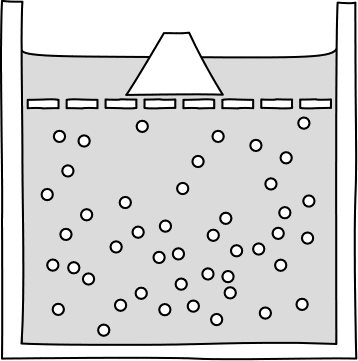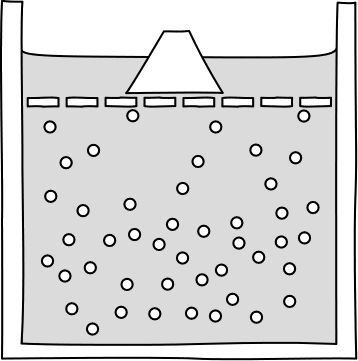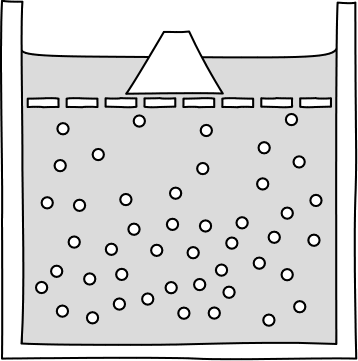
scattering of sugar molecules under their random thermal motion. Indeed in
dilute solutions, the sugar molecules form a system of a large number of
molecules that do not interact with oneanother--they are widely spaced in the
water because of the high dilution.
|
 |
|
A large number of molecules that do not interact?! This
is exactly the condition that we saw the molecules of an ideal gas had to obey in order for the ideal
gas law to obtain. So it should hold here as well. And it does!
The random, microscopic motions of sugar molecules that leads to
diffusion can be redescribed on a macroscopic level as a pressure,
just as is the case with an ideal gas. This pressure is the familiar
osmotic pressure so important in cell
biology. Consider a semi-permeable membrane that can pass water but
not sugar, such as the membrane in the figure opposite or a cell
wall. The (gray) water can pass freely through it, but sugar
molecules (the little white spheres) cannot. Through their collisions
with the membrane, the sugar molecules exert a pressure on the
membrane and the considerations that fix the size of the ideal gas
pressure are exactly the same as those that fix the size of the
osmotic pressure.
The osmotic pressure P exerted by n sugar molecules in a volume V of
water in dilute solution obeys the ideal gas
PV = nkT |
|
|
This osmotic pressure became central to Einstein's
derivation of the result (4) for sugar
diffusing in solution. To generate it, he imagined the same set up as
I have described above, dissolved sugar molecules in a gravitational
field. There are two processes acting on the sugar molecules.
First, the effect of gravity is to pull
the molecules downward. So they fall, as shown. A standard law in
fluid mechanics, Stokes' law, expresses just how fast they fall under
the pull of gravity. |
|
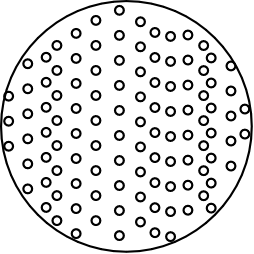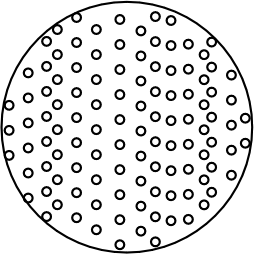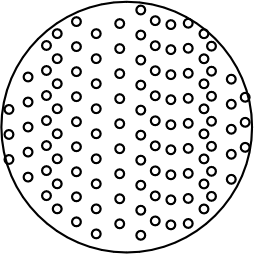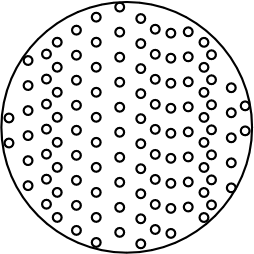 |
|
|
 |
|
Second, a diffusion process
scatters the falling sugar molecules. Its net effect is to send the
sugar molecules from regions of high concentration to regions of low
concentrations. That precludes the falling molecules accumulating too
much at the bottom of the vessel.
Einstein used the fact that dissolved sugar exerts an osmotic
pressure to determine the magnitude of this effect. The falling sugar
forms a density gradient. The ideal gas law asserts that pressure is
proportion to density, so there is an osmotic pressure gradient. And
that pressure gradient drives the sugar back up.
An equilibrium between the processes will
be established when the amounts of sugar transported by the two
processes in opposite directions are equal. The equation that sets
those two rates of transport equal turns out to be just the second
equation Einstein needed for the argument of his doctoral
dissertation:
(4) N= (RT/6 pi mu D) . 1/P
or in terms of what matters
(4) N =
(things that can be measured) x
1/P |
|
5. Einstein's Brownian Motion Paper
The argument and method of Einstein's dissertation was
indirect and cumbersome. Since the original
project of examining the viscosity of sugar solutions yielded one equation in
two unknowns, he needed to introduce analysis of a second sort of physical
process, diffusion, in order to get a result. To recall, he ended up with TWO
equations in TWO unknowns, N and P, the radius of a sugar molecule:
(3) N = (things that
can be measured) x 1/P3
(4) N = (other
things that can be measured) x 1/P
We could well imagine Einstein examining these two
unknowns, N and P, and lamenting that both are inaccessible to direct
measurement. In the case of sugar solutions, of course, the problem is
inescapable. To know one is to know the other; if we are ignorant of one we
do not know the other. But wait--what if we were
to apply this same analysis not to sugar solutions but to other solutions
whose "molecules" are so big that we might measure their size directly under
the microscope? That could be done. All we are really considering is a
suspension in water of very finely divided particles, perhaps even like the
tiny pollen grains Brown had observed under the microscope earlier in the
19th century. For these systems, there now only ONE unknown, N. Thermal
motions would lead such particles to diffuse through water and, using
equation (4) alone, Einstein could determine N from the measured rate of
their diffusion.
I do not know if this is the reasoning that brought
Einstein from the reflections of his doctoral dissertation to the Brownian
motion paper. But I can say that the path is obvious and direct, just as it
leads to a very much more adventurous result. Einstein is not longer
computing the size of molecules, he has found a process which it seems that
only a molecular kinetic theory of heat can
accommodate!
|
The remarkable fact is that Einstein could use exactly the same analysis for this process as
he had used for the diffusion of sugar. The suspended particles
consist of a large number of independent components--that you can see
them under the microscope does not alter that fact. So they will
exhibit thermal motions which in turn exert a pressure on a membrane
that does not allow them to pass.
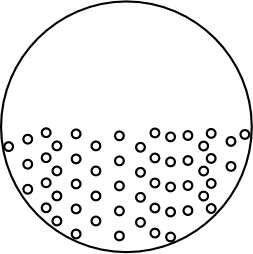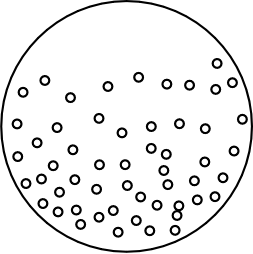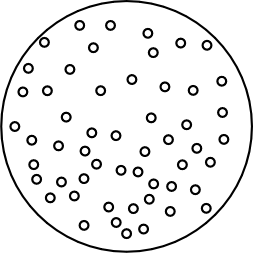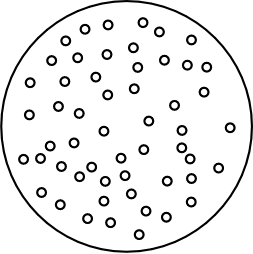
At this point, no more calculation is needed. The particles will
establish an equilibrium distribution in the gravitational field
exactly as did the sugar molecules. Once again we can characterize
that equilibrium by equating the rate at which the particles fall
under gravity with the rate at which diffusion scatters them back up.
The result is:
(4) N= (RT/6 pi mu D) . 1/P
as before. Since P is now observed, all Einstein needs is to measure
the rate of diffusion of the particles to recover D and then use (4)
to compute N. |
|
 |
|
|
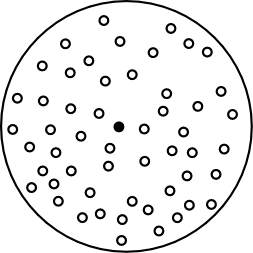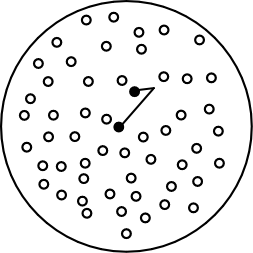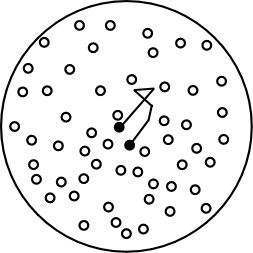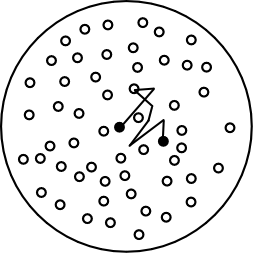 |
|
This last step of the computation of N proved the most
interesting. The thermal diffusion of these particles would manifest
under the microscope as a random jiggling
motion. Indeed Einstein conjectured that this was just the
motion Brown has noted for pollen grains, although in this first
paper Einstein lamented that he did not have enough data to be
sure.
For particles of size 0.001mm, Einstein predicted a displacement of
approximately 6 microns in one minute. |
|
6. The Importance of Einstein's Analysis of Brownian
Motion
Following the easy logic of the pathway from his
dissertation, we may overlook the momentous
importance of what has just transpired. Einstein had found an effect
that settled one of the major debates of the early 20th century!
In the course of the latter part of the 19th century,
Maxwell, Boltzmann and others had struggled to establish that their
statistical treatment of thermal processes deserved a
place in physics. It was a difficult struggle. For their statistical
accounts seemed to be at odds with established thermodynamics, grounded
squarely in experiment. Most notoriously, there were (then) two laws
fundamental laws of thermodynamics. The second law, the entropy principle,
expressed the notion that thermodynamic processes were directed in time.
Gases spontaneously expand to fill space. They do not spontaneously contract.
In the statistical approach, however, they do spontaneously contract, but
with very small probability. (We will see more of this shortly!) So Boltzmann
struggled to establish that this basic law of thermodynamics only held with
very high probability.
For Maxwell and Boltzmann, the project was to catch up with
thermodynamics and show that they could do what the thermodynamicists were
already doing without calling upon stories about atoms. Seen in this light,
the opposition of energeticists like Ostwald at the start of the 20th century
to atoms is quite understandable. They did not
seem to need atoms to do their physics; and presuming atoms required
compromising the basic laws of thermodynamics. So why play with the notion of
atoms when it brought pain but no gain?
Einstein now had found a way to turn
the tables. The strength of the thermodynamicists was their grounding
in experiment. Yet here was an experimental effect--the random thermal
motions of suspended particles--that could not be accounted for by ordinary
thermodynamic means. One had to resort to something like a molecular kinetic
account. Einstein pointed to this momentous outcome in rather dry language in
the introduction to his paper:
"If it is really possible to
observe the motion discussed here ... then classical thermodynamics can no
longer be viewed as strictly valid even for microscopically distinguishable
spaces, and an exact determination of the real size of a mole becomes
possible."
Here I follow Anne Kox's
analysis of Einstein's "eine exakte Bestimmung der wahren Atomgroesse" and
translate Atomgroesse as size of a mole.
In addition to this
foundational issue, there was a second theoretical bounty emerging from
Einstein's analysis of Brownian motion. In order to determine N, Einstein
needed to estimate the diffusion coefficient associated with the random
motion of the suspended particles. This required a statistical analysis of
the random jiggling of the particles.
|
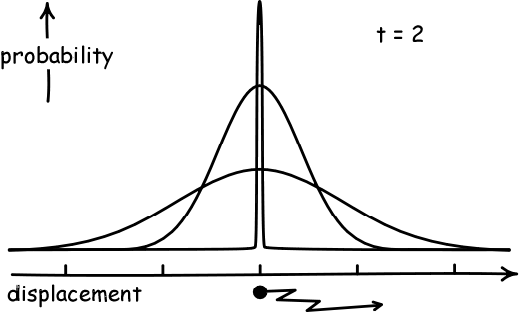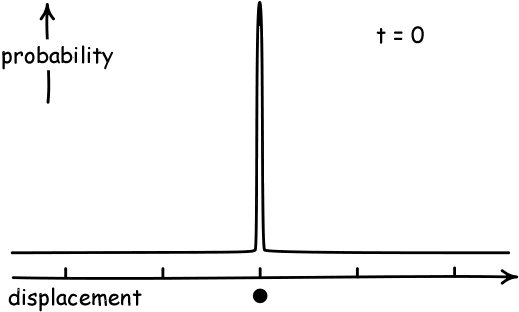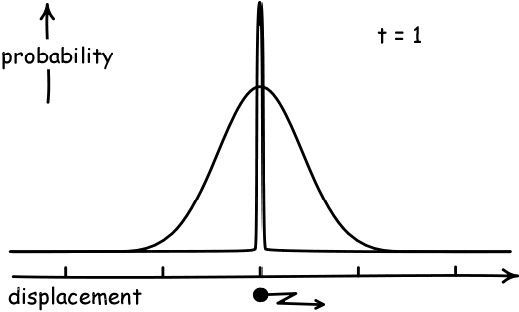 |
|
The analysis had to be probabilistic. If a particle starts at some
known position, we can at best specify the probabilities of it
straying ever further from that initial point. The curve representing
these probabilities is the familiar bell curve. As time t passes it
becomes more and more flattened, capturing the greater probability of
the particle straying from its initial position.
Einstein showed that this flattening of the curve is directly related
to the diffusion coefficient D. That is, the mean square displacement
is 2.D.t.
Through this analysis, Einstein's paper became one of the first
treatments of the problem of the "random walk" and one of the
founding documents in the new field of stochastic processes. |
|
Finally there were some interesting subtleties in this
random motion. First, the jiggles observed under the microscope were not the
result of collisions with individual water molecules. You might presume that the effect of very many
collisions with water molecules would rapidly average out to no effect at
all. That turns out to be mistaken. The statistical analysis shows that even
very many molecular collisions leaves a residual jiggle. Second, it is futile
to try to find the average speed of the jiggling particles. Speed is
displacement/time. Einstein's analysis shows that the average displacement is
proportional to the square root of time. So the ratio of
displacement/time varies as 1/(square root of time) and so goes to zero as
time gets large. So if we try to average out the jiggles to find an average
speed, we end up with averages that will get closer and closer to zero the
longer the time period we consider.
7. The Light Quantum Paper:
Einstein's Astonishing Idea
The great triumph of 19th century physics had been
Maxwell's electrodynamics. It established definitively the wave character of light, identifying it as propagation
in the electromagnetic field. It seemed impossible in the face of Maxwell's
great achievement that we could ever go back to a view of light such as
Newton held, that light consists of little corpuscles. Yet exactly this was
the astonishing idea of Einstein's 1905 light quantum paper.
Einstein had several bases for this idea. Some were
grounded directly in experiment. For example, he argued that we could best
account for the photoelectric effect if we
assumed that the energy of propagating light was spatially localized in
little packets of size hf, where h is Planck's constant and f is the
frequency of the light. This explanation of the photoelectric effect was
cited in the awarding of the Nobel Prize to Einstein in 1921: "for his
services to Theoretical Physics, and especially for his discovery of the law
of the photoelectric effect."
The core argument of Einstein's paper was different,
however. It drew on the thermodynamic behavior of high
frequency heat radiation. What Einstein noticed was that there was an
atomistic signature in its macroscopically measurable thermal properties. He
noted that high frequency heat radiation behaved thermodynamically as if it
consisted of independent, spatially localized quanta of energy of size hf.
This remark was the light quantum hypothesis.
The idea that the macroscopic properties of a system may
reveal its microscopic properties is not new. Indeed it has been present
throughout the discussion so far. That the system exerts a pressure governed
by the ideal gas law is just such a signature. It tells us that the system
consists of many, independent components and this signature can be found in
ideal gases, in dilute solutions and in systems of suspended particles. It
actually turns out to be present in high frequency heat radiation as well.
However its presence is harder to see. Heat
radiation does exert a pressure, known as radiation pressure. That pressure
is a function of the temperature and frequency of the radiation only. So we
may well wonder how the ideal gas law PV=nkT could apply to it, for the ideal
gas law clearly allows a volume dependence through the presence of the term
V.
It turns out the the ideal gas law still does apply to a high frequency heat radiation. That
fact is obscured by a novelty of heat radiation. The number of quanta in heat
radiation is not fixed in the way the number of components is fixed for other
systems such as an ideal gas. If we correct for that effect, compatibility
with the ideal gas law is restored.
|
 |
|
When an ideal gas undergoes a constant temperature
expansion, the ideal gas law PV=nkT tells us that the product of
pressure and volume PV stay the same. That is, the pressure decreases and the volume increases.
This is how we are used to seeing the ideal gas law manifested. |
|
|
When a system of high frequency heat radiation expands
at constant temperature, new energy quanta are
created in direct proportion to the volume V. That is, n/V
remains constant. The idea gas law now tells us that the pressure P
remains constant since we may write the law as P=(n/V)kT. The
immediate effect is that the satisfaction of the ideal gas law is
obscured since we are so used to the law telling us that pressure P
decreases in a constant temperature expansion. The atomic signature
is there; but it is in an unfamiliar form. |
|
 |
|
8. A New Atomic Signature
Einstein did not mention the
ideal gas law as an atomic signature for heat radiation. He did however
demonstrate the existence of another atomic signature to which high frequency
heat radiation did conform. He first illustrated that signature for the
familiar case of an ideal gas.
The statistical approach to gases differed from a purely
thermodynamic one, as noted above, in that it allows for gases to
spontaneously recompress, albeit with very small probability. The analysis is
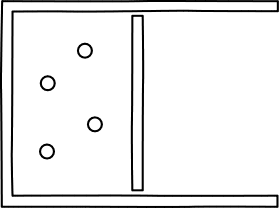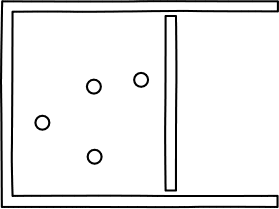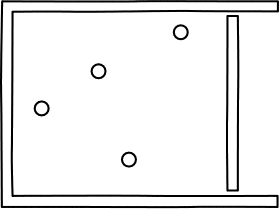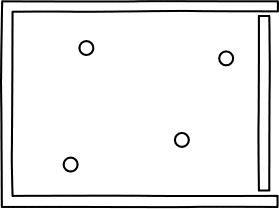
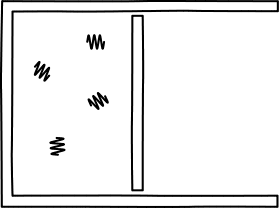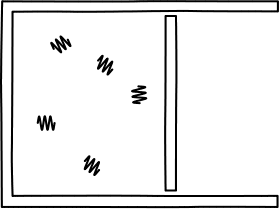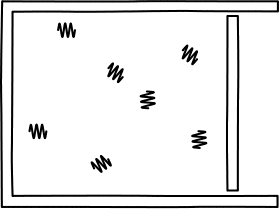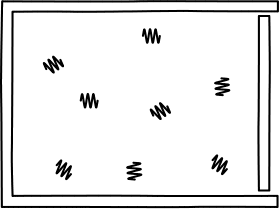
very simple. Consider an ideal gas with just four
molecules. The molecules will move randomly through the chamber shown and
will mostly be spread throughout it.
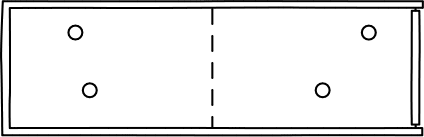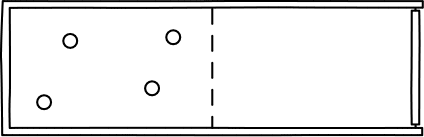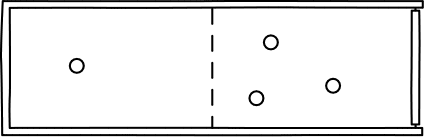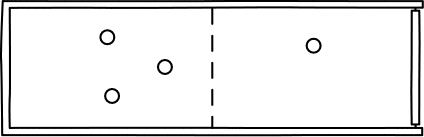
There is a probability of 1/2 that any
given molecule will be in the left half of the chamber when we check.
So the probability that all four of them will be there is just
(1/2) x (1/2) x (1/2) x (1/2) =
(1/2)4.
The key fact of independence is what allows us just to multiply all four
probabilities together to get the result. If we had n molecules, the
probability would be
(1/2) x (1/2) x (1/2) x ...(n times)... x (1/2) =
(1/2)n.
Since ordinary samples of gas will have of the order of n = 1024
molecules, this probability is fantastically small and we have no chance of
observing this fluctuation in ordinary life. (And that is fortunate, for otherwise our lives in
the air would like a small cork tossed about on a stormy sea!)
However the probability of this fluctuation is still quite
definite. An ideal gas can spontaneously compress to half its volume with
miniscule probability (1/2)n.
Statistical physics happens to give us another way to
determine this probability, without us actually having to see the spontaneous
recompression. The probability of the transition is related to a macroscopic thermodynamic quantity,
entropy. We need not here go into many details of the nature of this
quantity. All that matters for us is that entropy is a thermodynamic property
of thermal systems, just as is energy, and its value is routinely given in
tables of thermal properties of substances. I
will not pause here to rant about the unfortunate mythology of mystery that
surrounds the notion. A good part of it is due to plain old foggy thinking.
See my website, http://www.pitt.edu/~jdnorton for
details.
The Simplest Version of the Argument
The details of the next steps of Einstein's argument are a
little messy for people who don't like logarithms. So here's the very simplest version without logarithms.
The thermodynamic quantity entropy tells us what sorts of
transformations thermal systems will undergo. The basic rule is that thermal
systems will tend to states of higher entropy. So
the entropy difference between two states of a system gives us information on
the tendency of the system to move between the states. Indeed the "tendency"
can be given a quite precise measure as a probability. If we know the entropy
difference between two states of a system, we know the probability that the
system will spontaneously move between those two states.
| Now recall that the entropy of a system is an
ordinary thermodynamic quantity like energy. Just as you can measure
the energy content of some volume of radiation by a suitable
experiment, you can also measure the
entropy content of that system. |
That is just what Einstein did for heat radiation. More
precisely, he took other people's measures of entropy and used them to figure
out the entropy difference between two states: a
quantity of heat radiation of energy E at one, particular high frequency f
and a second quantity of heat radiation of the same energy E and frequency f,
but half the volume.
From the entropy change between those two states, Einstein
could infer that the probability of the quantity
of radiation spontaneously fluctuating to half its volume is just
(1/2)(E/hf). Written out more fully that is
(1/2) x (1/2) x (1/2) x ...(E/hf times)... x (1/2) =
(1/2)(E/hf)
Comparing this formula to the corresponding formula for n molecules, it is
almost impossible to avoid concluding that this quantity of high frequency
radiation consists of E/hf spatially localized radiation molecules--Einstein
called them "light quanta"--that move independently through the volume.
The picture to have in mind is:
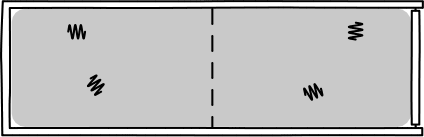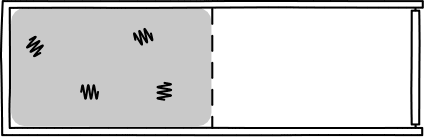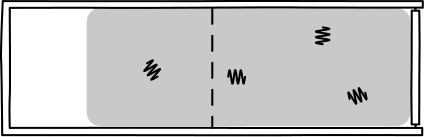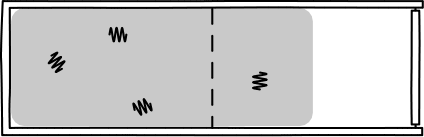
The best part is that the probability formula tells us
directly how big these light quanta are. The probability comes from
multiplying E/hf factors of (1/2) together. So we infer that the total energy
E of the radiation is divided into that many quanta of energy, each of size hf.
The Fancier Version of the Argument
Now here's the fancier version.
The entropy change between two states S is related to the
logarithm of the probability W of a spontaneous transition between the two
states by the formula
S = k log W.
Einstein judged this result so important that he named it "Boltzmann's Principle." That wonderful formula was
engraved on Boltzmann's gravestone; it is the bridge we need between the
macroscopic and the microscopic.
Apply this principle to the case of the ideal gas of n
molecules that spontaneously compresses to half its volume with probability W
= (1/2)n. We find that the difference in entropy between the gas
and that same gas occupying one half the volume is given by
(5) S = k.log W = k.log (1/2)n = - nk.log 2
While we arrived at this entropy difference by thinking about extremely
improbable fluctuations in the gas' volume, it can also be found in standard
thermodynamic treatises, derived entirely from
macroscopic properties of ideal gases, without any mention of
microscopic properties and very unlikely events. (In particular, you do not need to know the size of N
to get this formula. For nk = nm.R, where nm is the
number of moles and R is the ideal gas constant.) But now that we know
how to read the logarithmic dependence of entropy on volume of (5), we can
recognize it as a macroscopic signature of the spatially localized,
independent atoms in the ideal gas.
Einstein recognized this same
signature in a single frequency cut of high frequency heat radiation.
By drawing directly on experimental measurements of the thermal properties of
high frequency heat radiation, he noted that the entropy difference between
two quantities of radiation of energy E and frequency f, one at the full
volume and one at the half volume, is just:
(6) S = - (E/hf).k.log 2 = k log (1/2)(E/hf)
The analogy between formulae (5) and (6) is obvious.
Einstein had now found the
macroscopic signature of atoms in high frequency heat radiation. Comparing
equations (5) and (6), we immediately see that the heat radiation is governed
by a formula appropriate to a system consisting of E/hf independent
components. Or, to put it another way, it is as if the energy E of the
radiation is divided into independent, spatially localized components of
energy hf. This, you will recall, is just Einstein's light quantum
hypothesis, but now read from equations (5) and (6).
You should note how carefully
hedged Einstein's statement of the light quantum hypothesis is. Its
most careful formulation from his 1905 paper is:
"Monochromatic radiation of low density behaves--as long as Wien's radiation
formula is valid [i.e. at high values of frequency/temperature]--in a
thermodynamic sense, as if it consisted of mutually independent energy quanta
of magnitude [hf]."
Einstein is very careful to add many conditions: high frequency/temperature,
low density, "as if" and "in a thermodynamic sense."
That caution is very prudent. Einstein had not explained
away the quite prodigious body of evidence from the 19th century all pointing to the wavelike character of light. Indeed
that evidence will never go away. What Einstein eventually decided a few
years later is that both wave and particle characters are needed for a full
account of light. Sometimes light will behave like a wave; sometimes like a
localized particle; and sometimes both. That we now know as "wave-particle"
duality.
Modern readers often find it irresistible to jump from
these light quanta of 1905 to modern photons;
that is, to imagine that Einstein was just proposing that light really
consists of particles or corpuscles after all. That would be a risky jump for
all the reason just given. In addition, an essential part of the notion of a
photon is that it carries momentum. Nothing in Einstein's arguments so far
have established that his light quanta of 1905 also carry momentum. That
conclusion had to be established by further analysis and it came with
time.
9. Conclusion
Einstein published three papers in statistical physics in
1905. By any measure, their content is
extraordinary. In one form or another they contained the seeds of the new
theorizing in statistical physics of the twentieth century. They provided a
new method of estimating the size of molecules, a treatment of the diffusion
of solutes and small particles in viscous media, the identification of a
phenomenon that turned the tide of resistance to molecular kinetic methods in
physics, a foundational analysis in the new field of stochastic processes and
the demonstration of the granular character of electromagnetic radiation.
When faced with this wealth, it is hard not to be awed, let
alone to find a unifying theme that permeates the
work. My goal has been to display just such a theme, even if the theme does
not pass through the heart of every aspect of Einstein's achievement. That
theme is the simple idea that thermal systems consisting of many, spatially
localized, independent components have the same macroscopic properties, most
notably the satisfaction of the ideal gas law. This fact simplifies analysis
of many systems, since once the independence of the components is known, the
ideal gas law must follow, whether the system is a gas, dilute solution or
microscopically visible particles in suspension. And the inference can be
inverted. Once an atomic signature is seen, one can infer back to the
constitution of the system. In the case of high frequency heat radiation, the
presence of the atomic signature was so definite that it emboldened Einstein
to overthrow the great achievement of 19th century physics. He rejected
Maxwell's electrodynamics and its wave theory of light, in favor of a new and
still ill-formed quantum account of radiation.
Copyright John D. Norton, May 8, 2005. Section 8 revised May 2007.
Minor corrections, May 15, 2005; link to "How
big is an atom? June 17, 2006.












