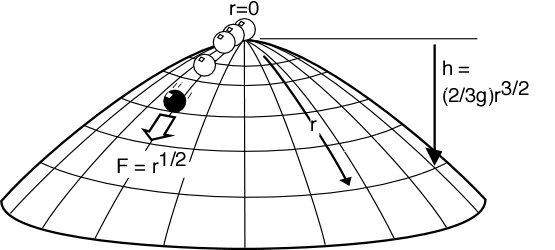
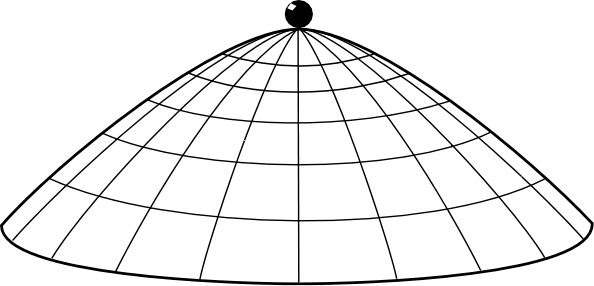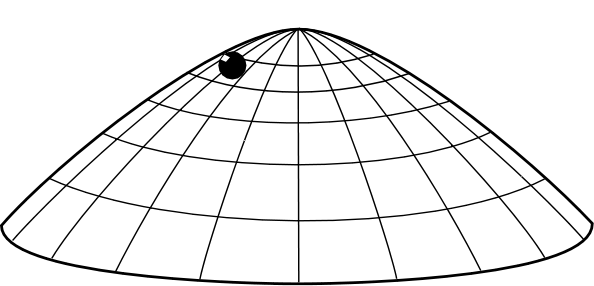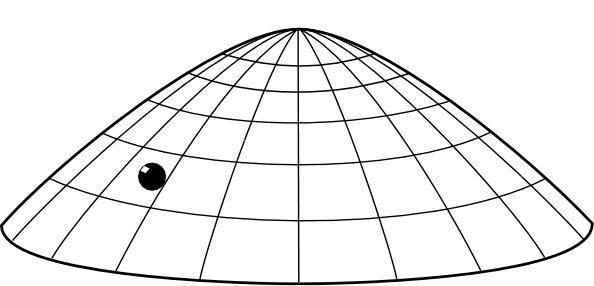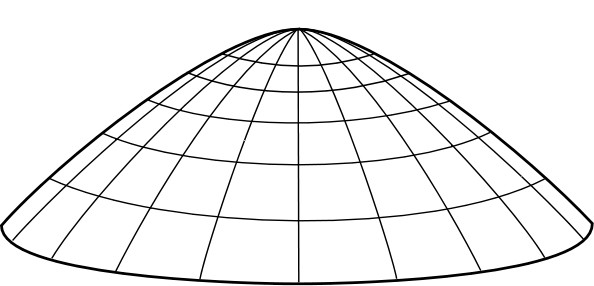
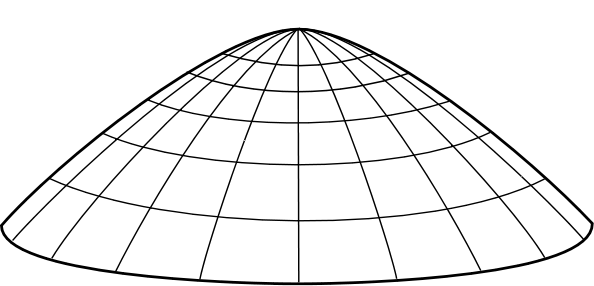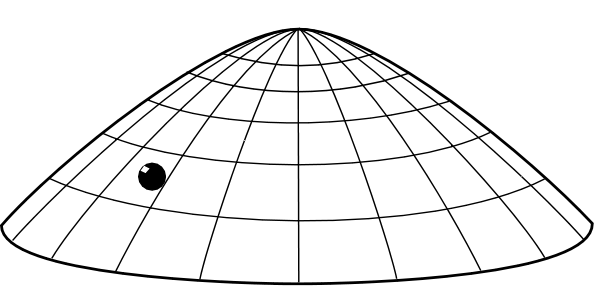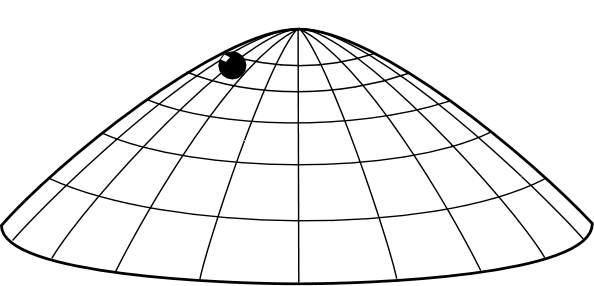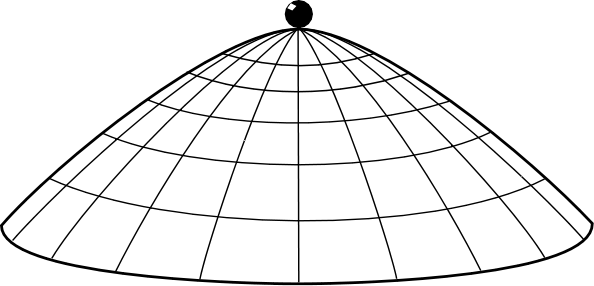
Figure 1a. Mass sliding on a dome
John D. Norton
Department of History and Philosophy of Science, University of Pittsburgh
Pittsburgh PA 15260. Homepage: www.pitt.edu/~jdnorton
This page is available at www.pitt.edu/~jdnorton/goodies
This page is based on Section 3 "Acausality in Classical Physics" of "Causation as Folk Science," Philosophers' Imprint Vol. 3, No. 4
http://www.philosophersimprint.org/003004/; to be reprinted in H. Price and R. Corry, Causation and the Constitution of Reality. Oxford University Press.
While exotic theories like quantum mechanics and general relativity violate our common expectations of causation and determinism, one routinely assumes that ordinary Newtonian mechanics will violate these expectations only in extreme circumstances if at all. That is not so. Even quite simple Newtonian systems can harbor uncaused events and ones for which the theory cannot even supply probabilities. Because of such systems, ordinary Newtonian mechanics cannot license a principle or law of causality. Here is an example of such a system fully in accord with Newtonian mechanics. It is a mass that remains at rest in a physical environment that is completely unchanging for an arbitrary amount of time--a day, a month, an eon. Then, without any external intervention or any change in the physical environment, the mass spontaneously moves off in an arbitrary direction, with the theory supplying no probabilities for the time or direction of the motion.
The dome of Figure 1a sits in a downward directed gravitational field, with acceleration due to gravity g. The dome has a radial coordinate r inscribed on its surface and is rotationally symmetric about the origin r=0, which is also the highest point of the dome. The shape of the dome is given by specifying h, how far the dome surface lies below this highest point, as a function of the radial coordinate in the surface, r. For simplicity of the mathematics, we shall set h = (2/3g)r3/2. (Many other profiles, though not all, exhibit analogous acausality.)

Figure 1a. Mass sliding on a dome
A point-like unit mass slides frictionlessly over the surface under the action of gravity. The gravitational force can only accelerate the mass along the surface. At any point, the magnitude of the gravitational force tangential to the surface is F = d(gh)/dr = r1/2 and is directed radially outward. There is no tangential force at r = 0. That is, on the surface the mass experiences a net outward directed force field of magnitude r1/2. Newton's second law, F = ma, applied to the mass on the surface, sets the radial acceleration d2r/dt2 equal to the magnitude of the force field:
(1) d2r/dt2 = r1/2
If the mass is initially located at rest at the apex r = 0, then there is one obvious solution of Newton's second law for all times t:
(2) r(t) = 0
The mass simply remains at rest at the apex for all time as shown:
Simplest solution: no motion
However, there is another large class of unexpected solutions. For any radial direction:
(3) r(t) = (1/144) (t-T)4 for t greater than or equal to T
= 0 for t less than or equal to T
where T is an arbitrarily chosen, positive constant. One readily confirms that the motion of (3) solves Newton's second law (1). See Note 6
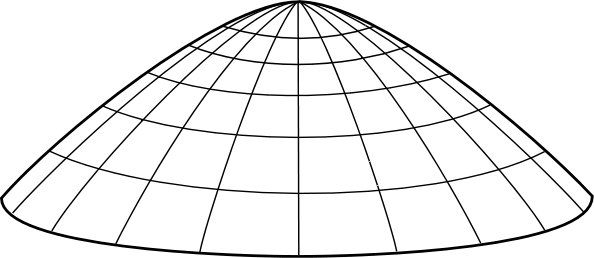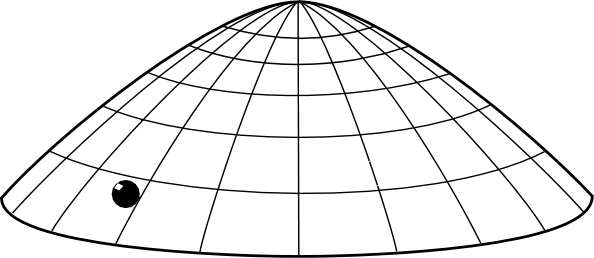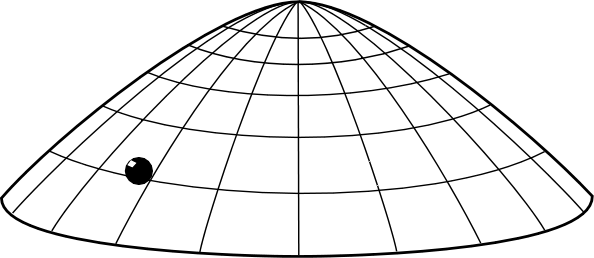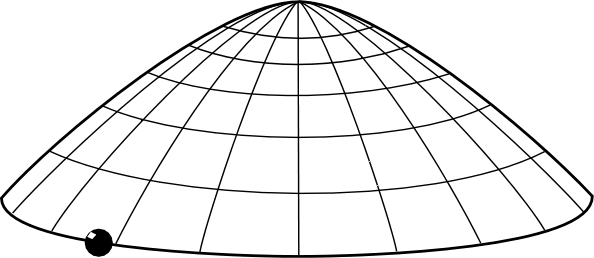
If we describe the solutions of (3) in words, we see they amount to a violation of the natural expectation that some cause must set the mass in motion. Equation (3) describes a point mass sitting at rest at the apex of the dome, whereupon at an arbitrary time t=T it spontaneously moves off in some arbitrary radial direction.
Spontaneous motion
Two distinct features of this spontaneous excitation require mention.
No cause. No cause determines when the mass will spontaneously accelerate or the direction of its motion. The physical conditions on the dome are the same for all times t prior to the moment of excitation, t=T, and are the same in all directions on the surface.
No probabilities. One might think that at least some probabilistic notion of causation can be preserved in so far as we can assign probabilities to the various possible outcomes. Nothing in the Newtonian physics requires us to assign the probabilities, but we might choose to try to add them for our own conceptual comfort. It can be done as far as the direction of the spontaneous motion is concerned. The symmetry of the surface about the apex makes it quite natural for us to add a probability distribution that assigns equal probability to all directions. The complication is that there is no comparable way for us to assign probabilities for the time of the spontaneous excitation that respect the physical symmetries of solutions (3). Those solutions treat all candidate excitation times T equally. A probability distribution that tries to make each candidate time equally likely cannot be proper--that is, it cannot assign unit probability to the union of all disjoint outcomes. See note 7. Or one that is proper can only be defined by inventing extra physical properties, not given by the physical description of the dome and mass, Newton's laws and the laws of gravitation, and grafting them unnaturally onto the physical system. See note 8.
The solutions (3) are fully in accord with Newtonian mechanics in that they satisfy Newton's requirement that the net applied force equals mass x acceleration at all times. But one may still worry that spontaneous acceleration somehow violates Newton's First Law:
In the absence of a net external force, a body remains at rest or in a state of uniform motion in a straight line.
It is natural to visualize "uniform motion in a straight line" over some time interval, but we will need to apply the law at an instant. At just one instant, the law corresponds to motion with zero acceleration. So the instantaneous form of Newton's First Law is:
In the absence of a net external force, a body is unaccelerated.
Returning to the concern, there is no net force on the mass at t=T, so, by this law, shouldn't the mass remain at rest? A more careful analysis shows the motions of (3) are fully in accord with Newton's First Law.
For times t less than or equal to T, there is no force applied, since the body is at position r=0, the force-free apex; and the mass is unaccelerated.
For times t > T, there is a net force applied, since the body is at positions r>0 not at the apex, the only force free point on the dome; and the mass accelerates in accord with F=ma.
But what of the crucial time t=T? The solutions of (3) entail that the acceleration a(t) of the mass is given by
(4) a(t) = (1/12)(t-T)2 for t greater than or equal to T
= 0 for t less than or equal to T
We confirm by substitution into (3) that at t=T, the mass is still at the force-free apex r=0 and, by substitution into (4), that the mass has an acceleration a(0) of zero. This is just what Newton's first law demands. At t=T, there is no force and the mass is unaccelerated. At any t>T, there is a nonzero force and the mass is accelerated accordingly.
Why is it so easy to be confused by this application of Newtonian mechanics? Our natural causal instinct is to seek the first instant at which the mass moves and then look for the cause of the motion at that instant. We are tempted to think of the instant t=T as the first instant at which the mass moves. But that is not so. It is the last instant at which the mass does not move. There is no first instant at which the mass moves. The mass moves during the interval t>T only and this time interval has no first instant. (Any candidate first instant in t>T, say t=T+epsilon for any epsilon>0, will be preceded by an earlier one, t=T+epsilon/2, still in t>T.) So there is no first instant of motion and thus no first instant at which to seek the initiating cause.
There is a simple way to see that the spontaneous motion of the mass is actually not that strange. Instead of imagining the mass starting at rest at the apex of the dome, we will imagine it starting at the rim and that we give it some initial velocity directed exactly at the apex. If we give it too much initial velocity, it will pass right over the apex to the other side of the dome. So let us give it a smaller initial velocity. We produce the trajectory T1:
Failed trajectory T1
The mass rises towards the apex, but before it arrives it loses its motion, momentarily halts and then falls back to the rim.
So we give it a little more initial velocity to produce trajectory T2:
Failed trajectory T2
The mass rises closer to the apex but does not reach it before momentarily halting and falling back.
We continue this process until we give the mass just the right initial velocity so that it rises up and momentarily halts exactly at the apex:
The trajectory is just right.
In this last case, we have ended up with the mass momentarily at rest at the one force free point on the dome, the one point where, if it is at rest, the mass can (but need not) remain at rest. So let us imagine that it does remain at rest once it arrives. We now have a trajectory in which the mass rises up to the apex, halts there and remains there at rest for any arbitrary time period we care to nominate. See note 9.
An important feature of Newtonian mechanics is that it is time reversible, or at least that the dynamics of gravitational systems invoked here are time reversible. This means that we can take any motion allowed by Newton's theory and generate another just by imagining that motion run in reverse in time. So let us do that with the motion we have just generated. That reversed motion corresponds to a mass that remains at rest at the apex of the dome for some arbitrary time period and then spontaneously moves off towards the rim. And that is just a qualitative description of one of the solutions of (3).
This time-reversal trick is powerful, but we must be cautious not to overrate it. It is best used just to make the acausal behavior plausible, while the proper mathematical analysis of (1), (3), and (4) proves it. The reason is that there is a loophole. The spontaneous motion can happen only on domes of the right shape, such as those of Figure 1a. It cannot happen on others such as a hemispherical dome. The time-reversal argument fails for these other cases, for a reason that is easy to overlook. As we proceed through the trajectories T1, T2, ... on a hemispherical dome, the time taken for the mass to rise to its momentary halt increases without bound. The final trajectory we seek, the one that momentarily halts at the apex, turns out to require infinite time. This means that the mass never actually arrives. Its time reverse displays a mass that has been in motion at all past times, without any spontaneous launches. The corresponding time for the dome of Figure 1a, however, is finite, so the analysis does succeed for this case.