
 |
|| Algorithm Tutorial || Algorithm Demo || System Help ||
Contents[Definition of Dijkstra's Algorithm] [Despcription of Algorithm] [Example] |
Definition of Dijkstra's Algortithm
"Dijkstra's algorithm, named after Dutch computer scientist Edsger Dijkstra who conceived it in 1959, is a graph search algorithm in order to solve the single-source shortest path problem for a graph with non negative edge path costs, It computes length of the shortest path from the source to each of the remaining vertices in the graph. This algorithm is often used in routing."[1]
Relevant concepts:
"The algorithm works by keeping for each vertex v the cost d[v] of the shortest path found so far between s and v. Initially, this value is 0 for the source vertex s (d[s]=0), and infinity for all other vertices, representing the fact that we do not know any path leading to those vertices (d[v]=? for every v in V, except s). When the algorithm finishes, d[v] will be the cost of the shortest path from s to v -- or infinity, if no such path exists. The basic operation of Dijkstra's algorithm is edge relaxation: if there is an edge from u to v, then the shortest known path from s to u (d[u]) can be extended to a path from s to v by adding edge (u,v) at the end. This path will have length d[u]+w(u,v). If this is less than the current d[v], we can replace the current value of d[v] with the new value. Edge relaxation is applied until all values d[v] represent the cost of the shortest path from s to v. The algorithm is organized so that each edge (u,v) is relaxed only once, when d[u] has reached its final value."[2]
"The algorithm maintains two sets of vertices S and Q. Set S contains all vertices for which we know that the value d[v] is already the cost of the shortest path and set Q contains all other vertices. Set S starts empty, and in each step one vertex is moved from Q to S. This vertex is chosen as the vertex with lowest value of d[u]. When a vertex u is moved to S, the algorithm relaxes every outgoing edge (u,v)."[2]
An example can explain the basic idea of alogrithm above and let user understand easily. The example will briefly explain each step that is taken and how the distance is calculated.
Consider the following example:
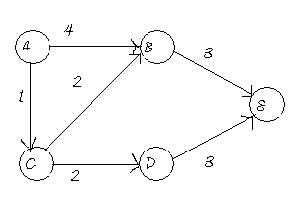
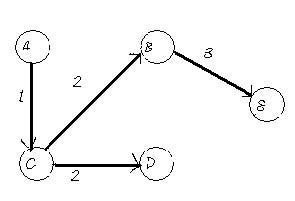
The above weighted graph has 5 vertices from A to E. The value between the two vertices is known as the weight between two vertices. For example the weight between A and C is 1. Using the above graph the DijkstraӮs algorithm is used to determine the shortest path from the source A to the remaining vertices in the graph.
Step 1
sDist[A]=0, the initial value to the source itself; sDist[B]= ”Ž, sDist[C]= ”Ž, sDist[D]= ”Ž, sDist[E]= ”Ž, the nodes not processed yet.
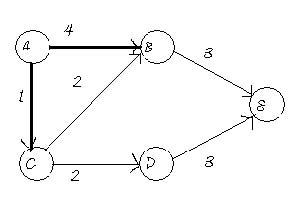
Step 2
Adj[A]={B,C}; computing the value of the adjacent vertices of the graph, sDist[B]=4; sDist[C]=1;
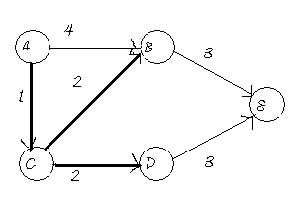
Step 3
Computation from vertex C, Adj[C] = {B, D}; sDist[B] > sDist[C]+ EdgeCost[C,B], 4 > 1+2 (True), Therefore, sDist[B]=3; sDist[D]=3;
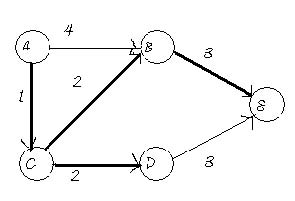
Step 4
Adj[B]={E}; sDist[E]=sDist[B]+EdgeCost[B,E]=3+3=6; Adj[D]={E}; sDist[E]=sDist[D]+EdgeCost[D,E]=3+3=6. This is same as the initial value that was computed so sDist[E] value is not changed.
Step 5
Adj[E]=0; means there is no outgoing edges from E, and no more vertices, algorithm terminated. Hence the path is presented in figure5.
Reference
[1]. http://en.wikipedia.org/wiki/Dijkstra's_algorithm
[2]. http://en.giswiki.net/wiki/Dijkstra's_algorithm#Description_of_the_algorithm