


Next: About this document ...
Up: No Title
Previous: Sylow's theorems
Let C=<x> be a cyclic group generated by the element x, with
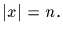 Denote by
Denote by
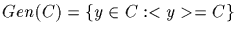 the set of
generators of C.
It is easy to see that
the set of
generators of C.
It is easy to see that
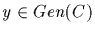 if and only if y=xm, where m,
if and only if y=xm, where m,
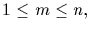 is a number relatively prime to n. If
is a number relatively prime to n. If
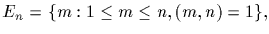 the mapping
the mapping
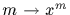 is a bijection from En
to Gen(C). The function
is a bijection from En
to Gen(C). The function
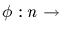
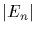 is called the Euler phi function.
Euler's function has two basic properties that are relatively
easy to verify:
is called the Euler phi function.
Euler's function has two basic properties that are relatively
easy to verify:
(a) For pk a prime power,
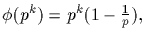 and
and
(b) For m and n relatively prime,
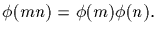
Theorem (Frobenius) - Berliner Sitzungsberichte, 1895, p. 984
If n divides the order of a group, then the number of elements in the
group whose orders divide n is a multiple of n.
Proof: Let G be a group of smallest order g for which the Theorem
fails. By this assumption the Theorem is true for all
groups H with
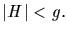 We call G a minimal counterexample. We
proceed to contradict the minimality of G, and thus conclude
that such G, in fact, does not exist.
We call G a minimal counterexample. We
proceed to contradict the minimality of G, and thus conclude
that such G, in fact, does not exist.
For the group G, let n be the largest factor of g for which the
Theorem fails. Since the Theorem is clearly true for
n=1 and n=g, it follows that
1<n<g. Let Nm denote the number of elements
in G whose order divides m. Furthermore, let p be a prime which
divides g. We have
Nnp=Nn+Nn',
where Nn' denotes the number of elements in G whose order divides
np but not n. We aim to show that
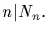 Since by the
inductive assumption
Since by the
inductive assumption
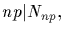 and therefore
and therefore
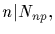 we conclude the
proof if we show that
we conclude the
proof if we show that
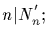 then n divides the difference
Nnp-Nn'=Nn.
then n divides the difference
Nnp-Nn'=Nn.
Let
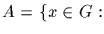 order of x divides np but does not divide
order of x divides np but does not divide 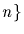 ;
;
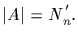 Write
Write
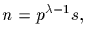 with (p,s)=1, that is, p and s are relatively prime.
Observe that if
with (p,s)=1, that is, p and s are relatively prime.
Observe that if 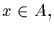 then
then
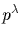 divides the order of x. To show that
divides the order of x. To show that
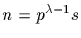 divides
divides
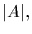 we first show that
we first show that
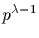 divides
divides
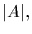 then
show that s divides
then
show that s divides
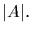 (Note also that if
(Note also that if
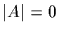 we are done.)
we are done.)
1. Let 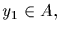
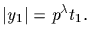 Then all the
Then all the
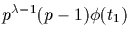 generators of
<y1> are in A; denote this set by A1. Select
generators of
<y1> are in A; denote this set by A1. Select
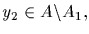
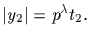 Again there are
Again there are
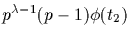 generators of <y2>, all of
them in A; call this set A2. Note that
generators of <y2>, all of
them in A; call this set A2. Note that
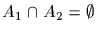 ,
for if
,
for if
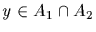 then
<y1>=<y>=<y2>, a contradiction. Since A is finite we have
then
<y1>=<y>=<y2>, a contradiction. Since A is finite we have
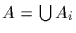 (disjoint union), and since
(disjoint union), and since
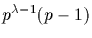 divides Ai for all i, we
conclude that
divides Ai for all i, we
conclude that
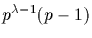 divides
divides
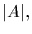 and hence
and hence
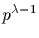 divides
divides
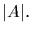
2. (a) If 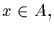
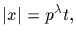 then x can be written uniquely as x=yz,
with y and z commuting and
then x can be written uniquely as x=yz,
with y and z commuting and
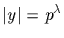 and
and
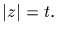 Indeed, the cyclic
group <x> can be written as a direct sum <x>=YZ, where Y is
a subgroup of <x> of order
Indeed, the cyclic
group <x> can be written as a direct sum <x>=YZ, where Y is
a subgroup of <x> of order
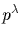 and Z is a subgroup of <x> of
order t. Thus x=yz, with
and Z is a subgroup of <x> of
order t. Thus x=yz, with 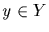 and
and 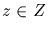 ,
as stated. Furthermore,
since y and z are in <x>, they are both powers of x.
,
as stated. Furthermore,
since y and z are in <x>, they are both powers of x.
As to uniqueness, if x=yz, with y and z as above, then
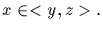 Since
Since
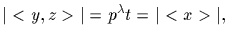 we conclude that
<y,z>=<x>. Thus y and z are in <x> and uniqueness follows from
the internal direct sum decomposition of
<x>=<y><z>. We call y
the
p-constituent of x.
we conclude that
<y,z>=<x>. Thus y and z are in <x> and uniqueness follows from
the internal direct sum decomposition of
<x>=<y><z>. We call y
the
p-constituent of x.
(b) For 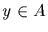 with
with
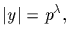 let
let
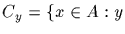 is the p-constituent of
is the p-constituent of
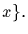 Note that if y1 and y2 are two distinct elements of order
Note that if y1 and y2 are two distinct elements of order
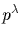 in
A, then
in
A, then
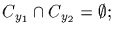 indeed, this follows from the uniqueness
of the p-constituent established in (a) above. We can now conclude
that the subsets Cy partition A.
indeed, this follows from the uniqueness
of the p-constituent established in (a) above. We can now conclude
that the subsets Cy partition A.
(c) Let 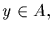
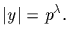 Denote by Ky the centralizer of y in G.
Clearly
Denote by Ky the centralizer of y in G.
Clearly
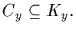 Let
Let
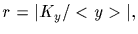 and let
d=gcd(r,s), that is, d is the greatest
common divisor of r and s. Since r<g, by the inductive assumption
there exist a
multiple of d, say cd, elements in Ky/<y> whose orders divide d.
Let
and let
d=gcd(r,s), that is, d is the greatest
common divisor of r and s. Since r<g, by the inductive assumption
there exist a
multiple of d, say cd, elements in Ky/<y> whose orders divide d.
Let 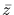 be such a coset of <y> in Ky. We can represent
be such a coset of <y> in Ky. We can represent 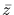 in the
form z<y>, with
in the
form z<y>, with
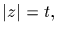 a divisor of d.
[Indeed,
a divisor of d.
[Indeed,
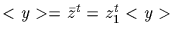 ,
and therefore
z1t=yi, for some i. We seek j such that z=z1yj
satisfies
1=zt=z1tyjt=yiyjt=yi+jt. Since
,
and therefore
z1t=yi, for some i. We seek j such that z=z1yj
satisfies
1=zt=z1tyjt=yiyjt=yi+jt. Since
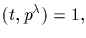 such a j
exists; take
j=-it-1 (mod
such a j
exists; take
j=-it-1 (mod
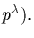 ]
Then
]
Then
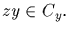 Each element of
Ky/<y> whose order divides d produces in this manner an element
of Cy. Thus
Each element of
Ky/<y> whose order divides d produces in this manner an element
of Cy. Thus
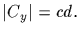
(d) Consider
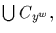 the disjoint union taken over all the conjugates
of y in G. We assert that s divides
the disjoint union taken over all the conjugates
of y in G. We assert that s divides 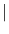
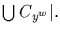 We have
We have
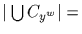
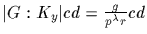 .
Since g is divisible by s and r, it
follows that gd is divisible by rs. Hence s is a divisor of
.
Since g is divisible by s and r, it
follows that gd is divisible by rs. Hence s is a divisor of
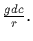 Since
s and
Since
s and
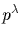 are relatively prime, s must also be a factor of
are relatively prime, s must also be a factor of
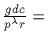
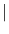
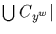 .
In view of (b) above, this shows that s divides
.
In view of (b) above, this shows that s divides
 This ends the proof.
This ends the proof.
By making use of the Möbius function we can obtain an expression
for the number of elements whose order is exactly n in terms of the
number of elements whose orders divide the divisors d of n.
Specifically, denote by f(d) the number of elements whose orders are
exactly n. Let h(d) denote the number of elements whose orders
divide d. Clearly we have,
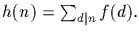 Möbius inversion now
yields
Möbius inversion now
yields
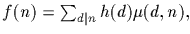 where
where 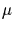 is defined to be 0, unless n/d
is a product of k distinct primes, in which case it equals (-1)k.
Frobenius' Theorem informs us that h(d)=m is a multiple of d.
We thus conclude as follows:
is defined to be 0, unless n/d
is a product of k distinct primes, in which case it equals (-1)k.
Frobenius' Theorem informs us that h(d)=m is a multiple of d.
We thus conclude as follows:
* If n divides the order of a group, then the number of elements of
order exactly n is equal to
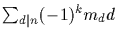 . Here the sum is over only
those divisors d of n with the property that n/d is a product of
any number (k, say) of
distinct primes. Furthermore, m is the number of elements whose
orders divide d.
. Here the sum is over only
those divisors d of n with the property that n/d is a product of
any number (k, say) of
distinct primes. Furthermore, m is the number of elements whose
orders divide d.



Next: About this document ...
Up: No Title
Previous: Sylow's theorems
Gregory Constantine
1998-09-01