


Next: Simplicity of the Alternating
Up: No Title
Previous: The isomorphism theorems
Let S be a set. A bijection
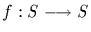 is called a permutation. Let
is called a permutation. Let
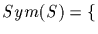 permutations on S
permutations on S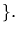 If
If
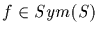 and
and
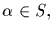 then
then
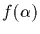 denotes the
image of
denotes the
image of 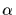 under f. The set Sym(S) forms a group under composition of
mappings, called the symmetric group on S.
under f. The set Sym(S) forms a group under composition of
mappings, called the symmetric group on S.
We say that the group G acts on the set S if there is a
homomorphism
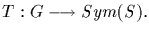 For
For 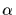 in S and g in G we abbreviate by
writing
in S and g in G we abbreviate by
writing
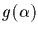 in place of
in place of
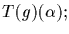 if h is also in G we have
if h is also in G we have
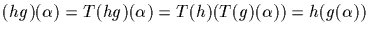 .
If kerT=1 we say that G
acts faithfully.
.
If kerT=1 we say that G
acts faithfully.
Define a subgroup
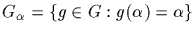 and call it the stabilizer of
and call it the stabilizer of
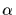 in G. Further define
in G. Further define
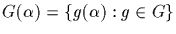 and call this subset of S
the orbit of
and call this subset of S
the orbit of 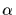 under the action of G.
under the action of G.
* Under a group action the set S decomposes into a disjoint union of orbits.
Indeed, pick an
element 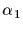 of S and produce its orbit under the action of G; pick
another element
of S and produce its orbit under the action of G; pick
another element 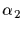 of S outside this orbit and produce its orbit (the
two orbits are easily seen to be disjoint, since
of S outside this orbit and produce its orbit (the
two orbits are easily seen to be disjoint, since
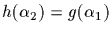 implies
implies
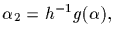 a contradiction); proceed until S is exhausted.
a contradiction); proceed until S is exhausted.
* The cardinality (or length) of the orbit is equal to the index of
the stabilizer. [Specifically, we assert that
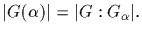 ]
]
This follows by
observing that 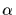 is sent into
is sent into
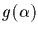 by exacly those group elements that
are in the coset
by exacly those group elements that
are in the coset
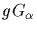 .
.
* (The class equation)
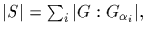 where
where 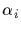 is a representative
from orbit i.
is a representative
from orbit i.
Indeed, S is the disjoint union of orbits. Its cardinality is, therefore,
the sum of the lengths of these orbits, which are indices of stabilizers
of orbit representatives.
* The stabilizers of two elements from the same orbit are conjugate
in G. [Specifically,
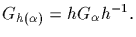 ]
]
The map
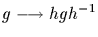 is a
bijection between
is a
bijection between
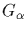 and
and
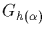 ,
which allows us to conclude that
,
which allows us to conclude that
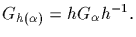
The homomorphic image T(G) is called a permutation representation
of the group G on the set S. We call T(G) a permutation group on S.
A permutation group on a set S is called transitive if for
any two elements of S there exists an element of the group sending
one into the other.
When the group element g is viewed as a permutation, the elements
of S that it fixes are called the fixed points of g.
A transitive group is regular if the only element of the
group which has fixed points is the identity.



Next: Simplicity of the Alternating
Up: No Title
Previous: The isomorphism theorems
Gregory Constantine
1998-09-01